이 글은 2Star WorstPerform 풋옵션 가격: Closed form #3 (Python Code)
2Star WorstPerform 풋옵션 가격: Closed form #3 (Python Code)
이번 글은 2Star WorstPerform 풋옵션 가격: Closed form #1 2Star WorstPerform 풋옵션 가격: Closed form #2 에서 살펴보았던 2Star WorstPerform Put option을 직접 코딩해 본 결과를 소개하는 글입니다. 먼저 Closed form을
sine-qua-none.tistory.com
에서 이어집니다. 저번 글에서는 2개의 기초자산의 WorstPerform의 풋옵션 가격을 여러 방법으로 계산해 보았는데, 이 글에서는 FDM 방법을 써서 구하는 방법을 알아보겠습니다.
파생상품의 가격 결정식이 Heat Equation의 형태로 주어진다는 것을 생각하면, [수학의 재미/아름다운 이론] - 2차원 Heat Equation의 풀이 #1 : Operator Splitting Method(OSM)
2차원 Heat Equation의 풀이 #1 : Operator Splitting Method(OSM)
예전 글에서 우리는 Heat Equation(열방정식)을 FDM으로 해결하는 방법을 알아본 적이 있습니다. 2022.08.01 - [수학의 재미/아름다운 이론] - FDM #7, Heat Equation의 풀이(3) FDM #7, Heat Equation의 풀이(3) 이 글은
sine-qua-none.tistory.com
에서 힌트를 얻어, 2개 기초자산을 가지는 파생상품의 가격을 OSM 방법으로 풀 수 있을 것 같습니다. 우선, 2Star WorstPerform풋옵션이 무엇인지 복습해 보죠.
2 Star WorstPerform 풋옵션
두 기초자산 Xt,Yt가 있을 때, 기준가를 각각 X0,Y0라 합니다. 이때 행사가 K이고 만기 T인 풋옵션의 만기 페이오프는
max
으로 주어집니다. 여기서
wp(t) = \min(X(t)/X_0 , Y(t)/Y_0)
입니다. 앞선 글에서 이 풋옵션의 가격을 Closed form, MC 방법으로 구해보았습니다.
| Closed form | ① 2Star WorstPerform 풋옵션 가격: Closed form #1 ② 2Star WorstPerform 풋옵션 가격: Closed form #2 ③ 2Star WorstPerform 풋옵션 가격: Closed form #3 (Python Code) |
| MC | 2Star WorstPerform 풋옵션 가격: 시뮬레이션 |
이제 FDM으로 풀어보겠습니다. 어떻게 접근할까요?
2 Star 파생상품의 가격 결정식
우선, 2개의 기초자산을 갖는 파생상품의 가격 결정식을 알아봅시다. 해당 내용은
2023.01.13 - [금융공학] - 여러 개의 기초자산을 가지는 파생상품 가격결정식
여러개의 기초자산을 가지는 파생상품 가격결정식
이번 글에서는 여러 개의 지수/주식을 기초자산으로 하는 파생상품의 가격 결정식을 소개할까 합니다. 하나의 기초자산을 가지는 파생상품 결정식은 다음의 글에서 다룬 바 있습니다. 2022.08.02 -
sine-qua-none.tistory.com
에서 찾을 수 있습니다.
두 기초자산 프로세스를
\begin{align} dX_t &= (r-q_1)dt + \sigma_1 dW_1(t) \\ dY_t &= (r-q_2)dt+\sigma_2 dW_2(t)\end{align}
라 합시다(r은 무위험 이자율 dW_1(t)\cdot dW_2(t) = \rho dt, 즉 X_t, Y_t 수익률의 상관계수는 \rho인 상황입니다.)
위의 링크된 글에 따르면 만기 페이오프 f(x,y)를 갖는 파생상품의 가치 u(t,x,y)는
\begin{align} \frac{\partial u}{\partial t} &+ (r-q_1) x\frac{\partial u}{\partial x}+ (r-q_2) y\frac{\partial u}{\partial y}\\ & + \frac12\sigma_1^2 x^2 \frac{\partial^2 u}{\partial x^2} +\frac12\sigma_2^2 y^2 \frac{\partial^2 u}{\partial y^2} +\rho\sigma_1\sigma_2 xy \frac{\partial^2 u}{\partial x \partial y} -ru =0,\tag{BS} \end{align}
u(T,x,y)=f(x,y)\tag{TC}
입니다. (BS)은 Black Scholes Equation이라는 뜻, (TC)은 terminal condition이라는 뜻입니다.
그런데 예전 글에서 살펴본 논리대로라면, 위의 식 (BS)는 바로 Heat Equation입니다.
게다가 Heat Equation은 FDM의 방법을 사용하여 풀 수 있다고 하였습니다. 바로 아래의 글이었죠.
2023.02.06 - [수학의 재미/아름다운 이론] - 2차원 Heat Equation의 풀이 #1 : Operator Splitting Method(OSM)
2차원 Heat Equation의 풀이 #1 : Operator Splitting Method(OSM)
예전 글에서 우리는 Heat Equation(열방정식)을 FDM으로 해결하는 방법을 알아본 적이 있습니다. 2022.08.01 - [수학의 재미/아름다운 이론] - FDM #7, Heat Equation의 풀이(3) FDM #7, Heat Equation의 풀이(3) 이 글은
sine-qua-none.tistory.com
위 글에서는 Heat Equation 스타일의 편미분 방정식을 이산화 시켜 OSM 방법으로 풀 수 있음을 설명했습니다. 이제 식 (BS) 이 친구를 이산화(discretization) 하여 봅시다.
편미분 방정식 (BS)의 이산화
자산이 2개인 만큼 t, x, y에 대한 3차원 그리드를 생각해야 합니다. 아래와 같이 각 변수를 분할합니다.
0=t_0<t_1<\cdots<t_{N-1}<t_n = T~,~~~ t_1-t_0 = k
x_{\min} = x_0 < x_1<\cdots <x_{I-1}<x_I = x_{\max}~,~~~ h_1 = x_1-x_0
y_{\min} = y_0 < y_1<\cdots <y_{I-1}<y_I = y_{\max}~,~~~ h_2 = y_1-y_0
위의 식 (BS)는 initial condition이 아닌 TERMINAL condition (TC)를 갖는 것에 착안하여 시점에 대해 backward로 풀어내려 오는 방법을 쓰겠습니다.
또한 x,y 두 변수가 있는 관계로 OSM 방법을 써서 변수 분리를 시키겠습니다. 그러기 위해서는
n과 n+1 시점 사이에 n+\frac12 필요
합니다.

위의 그림처럼
○ n+1에서 n+1/2 시점까지 backward로 x에 관하여 푼다.
○ n+1/2에서 n시점까지 backward로 y에 대해 푼다
그런데 문제가 있습니다. 아래 표를 보시죠. 식 (BS)를 분해해보면
| t에 대한 식 | \frac{\partial u}{\partial t} | |
| x에 대한 식 | (r-q_1) x\frac{\partial u}{\partial x} + \frac12\sigma_1^2 x^2 \frac{\partial^2 u}{\partial x^2} | n+1에서 n+1/2까지 |
| y에 대한 식 | (r-q_2) y\frac{\partial u}{\partial y}+\frac12\sigma_2^2 y^2 \frac{\partial^2 u}{\partial y^2} | n+1/2에서 n까지 |
| 기타 이도저도 아닌 식 | \rho\sigma_1\sigma_2 xy \frac{\partial^2 u}{\partial x \partial y} -ru | ??? |
과연 저 이도저도 아닌 식은 어떻게 처리해야 하는가입니다. x, y가 혼재되어 있어서 혼란스럽습니다.
또 기타 이도저도 아닌 식은 어떻게 이산화 시켜야 될까요.
Cross Term의 이산화
x,y가 섞여 있는
\frac{\partial^2 u}{\partial x \partial y}
을 cross term이라 합니다. 이것은 어떻게 이산화가 될까요? 점 (x,y)에서
\frac{\partial^2 u}{\partial x \partial y }(x,y) = \frac{\partial}{\partial x} \left( \frac{\partial u}{\partial y}\right)(x,y)
입니다.
그런데 작은 수 h_2에 대해서
\frac{\partial u}{\partial y} (x,y) \approx \frac{u(x,y+h_2)-u(x,y-h_2)}{2h_2}
입니다. 이것을 다시 \frac{\partial}{\partial x}를 취해보면,
\begin{align} \frac{\partial^2 u}{\partial x \partial y }&(x,y) = \frac{\partial}{\partial x} \left( \frac{\partial u}{\partial y}\right)(x,y)\\ & = \frac{\partial}{\partial x} \left( \frac{u(x,y+h_2)-u(x,y-h_2)}{2h_2} \right)\\ & = \frac{1}{2h_1} \left( \frac{u(x+h_1,y+h_2)-u(x+h_1,y-h_2)}{2h_2} - \frac{u(x-h_1,y+h_2)-u(x-h_1,y-h_2)}{2h_2} \right)\\ & = \frac{u(x+h_1,y+h_2)-u(x+h_1,y-h_2) -u(x-h_1,y+h_2)+u(x-h_1,y-h_2)}{4h_1h_2} \end{align}
이도 저도 아닌 식을 분할 반영
x나 y로 명쾌히 나눠지지 않는 항인
\rho\sigma_1\sigma_2 xy \frac{\partial^2 u}{\partial x \partial y} -ru
은 절반씩 다음과 같이 나눕니다.
| n+1에서 n+1/2까지 | x에 대한 식에 | \frac12\rho\sigma_1\sigma_2 xy \frac{\partial^2 u}{\partial x \partial y} -\frac12ru |
| n+1/2에서 n까지 | y에 대한 식에 | \frac12\rho\sigma_1\sigma_2 xy \frac{\partial^2 u}{\partial x \partial y} -\frac12ru |
절반씩 나누는 게 가장 간명해서 그렇지 위/아래 순서대로 \lambda, 1-\lambda로 나누는 방법도 가능합니다.
이산화
늘 그래왔듯이
u(t_n, x_i, x_j) := u_{ij}^n
이라 표기합시다. 그리고 식 (BS)를 아래와 같이 이산화 합니다.
\begin {align} \frac{u_{ij}^{n+1}-u_{ij}^{n+1/2}}{k} & + \mathcal{L}_x u_{ij}^{n+1/2} =0 \tag{1}\\ \frac{u_{ij}^{n+1/2}-u_{ij}^{n}}{k} & + \mathcal{L}_y u_{ij}^{n} =0\tag{2} \end{align}
여기서
\begin{align} \mathcal{L}_x u_{ij}^{n+1/2} = (r-q_1)& x_i\frac{u_{i+1,j}^{n+1/2} - u_{i-1,j}^{n+1/2}}{2h_1} + \frac12 \sigma_1^2x_i^2 \frac{u_{i+1,j}^{n+1/2}-2u_{ij}^{n+1/2}+u_{i-1,j}^{n+1/2}}{h_1^2} \\ & +\frac12 \rho x_iy_j \frac{u_{i+1,j+1}^{n+1}-u_{i+1,j-1}^{n+1}-u_{i-1,j+1}^{n+1}+u_{i-1,j-1}^{n+1}}{4h_1h_2} -\frac12 r u_{ij}^{n+1/2} \end{align}
이고
\begin{align} \mathcal{L}_y u_{ij}^{n} = (r-q_2)& y_j\frac{u_{i+1,j}^{n} - u_{i-1,j}^{n}}{2h_2} + \frac12 \sigma_2^2 y_j^2 \frac{u_{i+1,j}^{n}-2u_{ij}^{n}+u_{i-1,j}^{n}}{h_2^2} \\ & +\frac12 \rho x_iy_j \frac{u_{i+1,j+1}^{n+1/2}-u_{i+1,j-1}^{n+1/2}-u_{i-1,j+1}^{n+1/2}+u_{i-1,j-1}^{n+1/2}}{4h_1h_2} -\frac12 r u_{ij}^{n} \end{align}
입니다. \mathcal{L}_x u_{ij}^{n+1/2}, \mathcal{L}_y u_{ij}^{n}는 각각 n+1/2 시점레벨과 n시점 레벨을 중심으로 이산화를 시켰는데, 유독 3번째 항인 cross term들은 각각 n+1, n+1/2 시점에서 이산화 시켰습니다. 이는 계산의 편의를 위한 것으로서
cross term들은 이미 결정된 알려진 값으로 가정을 하고 Thomas Algorithm를 푸는 것
입니다. 참고로, 식(1), (2)를 더해보면, 식 (BS)를 얻을 수 있습니다.
(1) 번 식을 정리하면 아래와 같음
\alpha_i u_{i-1,j}^{n+1/2} +\beta_i u_{ij}^{n+1/2} +\gamma_i u_{i+1,j}^{n+1/2} = \eta_i
\begin{align} \alpha_i &= -\frac{r-q_1}{2h_1}+\frac{\sigma_1x_i^2}{2h_1^2}\\ \beta_i & = -\frac1k-\frac{\sigma_1x_i^2}{h_1^2}-\frac r2\\ \gamma_i&=\frac{r-q_1}{2h_1}+\frac{\sigma_1x_i^2}{2h_1^2}\\ \eta_i &= -\frac1ku_{ij}^{n+1} -\frac12 \rho x_iy_j \frac{u_{i+1,j+1}^{n+1}-u_{i+1,j-1}^{n+1}-u_{i-1,j+1}^{n+1}+u_{i-1,j-1}^{n+1}}{4h_1h_2} \end{align}
(2) 번 식을 정리하면 아래와 같음
\alpha_j u_{i,j-1}^{n} +\beta_j u_{ij}^{n} +\gamma_j u_{i,j+1}^{n} = \eta_j \begin{align} \alpha_j &= -\frac{r-q_2}{2h_2}+\frac{\sigma_2y_j^2}{2h_2^2}\\ \beta_j & = -\frac1k-\frac{\sigma_2y_j^2}{h_2^2}-\frac r2\\ \gamma_j&=\frac{r-q_2}{2h_2}+\frac{\sigma_2y_j^2}{2h_2^2}\\ \eta_j &= -\frac1ku_{ij}^{n+1/2} -\frac12 \rho x_iy_j \frac{u_{i+1,j+1}^{n+1/2}-u_{i+1,j-1}^{n+1/2}-u_{i-1,j+1}^{n+1/2}+u_{i-1,j-1}^{n+1/2}}{4h_1h_2} \end{align}
당연히 위 박스의 (\alpha_i,\beta_i,\gamma_i)와 아래박스의 (\alpha_j, \beta_j, \gamma_j)는 서로 다른 기호이지만, 이해의 편의를 위해 같은 기호를 썼습니다.
종합하면 다음과 같이 푸는 것입니다.
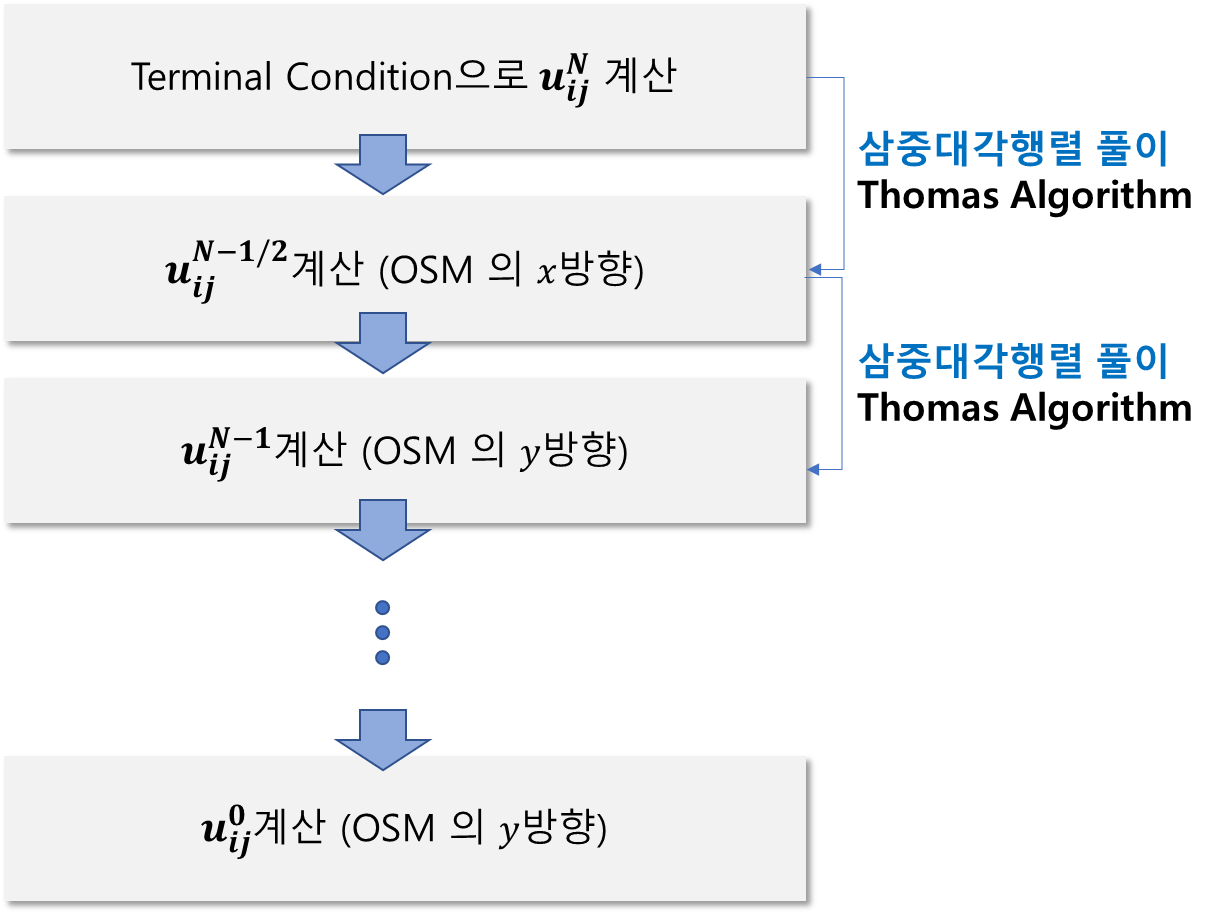
경계조건은 어떻게 하나?
예전 글에서 FDM의 경계 조건을 다룬 바가 있습니다. 그 중 경계조건이 선형이 되도록, 즉 두 번 미분한 값이 0 이 되도록 하는 방법을 Neumann condition(노이만 조건)이라 부르며 이 조건을 사용하여 경계치를 설정해 보도록 하겠습니다.
임의의 time level n에 대하여, 또 모든 i, j에 대해,
\begin{align} u_{2,j}^n -2u_{1,j}^n +u_{0,j}^n &=0\\ u_{I,j}^n -2u_{I-1,j}^n +u_{I-2,j}^n &=0\\ u_{i,2}^n-2u_{i,1}^n +u_{i,0}^n&=0\\ u_{i,J}^n-2u_{i,J-1}^n +u_{i,J-2}^n&=0 \end{align}
을 경계조건이라 봅니다. 즉, x_1, x_{I-1} 에서 x축 방향으로 선형, y_1, y_{J-1}에서 $y축 방향으로 선형 (2번 미분한 값이 0)이 되도록 설정하는 것입니다.
이제 다음 글에서 직접 Python code를 통해 2 Star WorstPerform Put option의 가치를 계산해 보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 두드림 ELS? Do Dream? 2X 드림! : 이론가 계산하기 #1 (0) | 2023.03.15 |
|---|---|
| 두드림 ELS? Do Dream? 2X 드림! (0) | 2023.03.14 |
| 워스트포퍼머의 기댓값 #2 : Python Code (0) | 2023.01.25 |
| 워스트포퍼머의 기댓값 (0) | 2023.01.22 |
| 2Star WorstPerform 풋옵션 가격: Closed form #3 (Python Code) (0) | 2023.01.21 |



댓글