예전 글에서 우리는 Heat Equation(열방정식)을 FDM으로 해결하는 방법을 알아본 적이 있습니다.
2022.08.01 - [수학의 재미/아름다운 이론] - FDM #7, Heat Equation의 풀이(3)
FDM #7, Heat Equation의 풀이(3)
이 글은 2022.08.01 - [수학의 재미/아름다운 이론] - FDM #6, Heat Equation의 풀이(2) FDM #6, Heat Equation의 풀이(2) 이 글은 2022.07.30 - [수학의 재미/아름다운 이론] - FDM #5, Heat Equation의 풀이(1) FDM #5, Heat Equation
sine-qua-none.tistory.com
시점 $t$와 변위 $x$ 두 변수로 이루어진 함수 $u(t,x)$가 Heat Equation을 만족한다는 것은
$$\frac{\partial u}{\partial t}(t,x) = \frac{\partial^2 u}{\partial x^2}(t,x) $$
를 만족한다는 뜻입니다. 물론 적절한 초기조건(initial condition)과 경계조건(boundary condition)이 주어지면 해 $u(t,x)$가 하나로 결정됩니다.
그런데 Heat Equation은 말 그대로 열이 이동하는 방식을 표현한 관계식이기 때문에 열이 평면이나 공간 등에서 어떻게 움직이는지를 표현할 때 훨씬 자주 쓰입니다. 따라서 다차원 Heat Equation을 해결해야 하는 경우가 많은데요.
이번글에서 다차원 중, 2차원에서의 Heat Equation에 대해 알아보도록 하겠습니다.
아래 그림은 공돌이의 수학정리노트 블로그에서 담아왔습니다. 너무 멋지네요.

2차원 Heat Equation
주어진 2차원 평면 $(x,y)$에 시점 $t$가 흐르며 열 함수 $u(t,x,y)$가 이 퍼져나가는 관계식은 아래처럼 표현이 됩니다.
▲ 관계식
$$\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} ~,~ 0\leq t\leq T, 0\leq x \leq a~,~ 0\leq y \leq b$$
▲ 경계조건(boundary condition)
$$ u(t, x, 0) =0, u(t,x,b) =0, u(t,0,y) =0, u(t,a,y)=0$$
▲ 초기조건(initial condition)
$$u(0,x,y) = f(x,y) $$
그림으로 표현하면, 경계조건은 아래와 같이 임의의 시점 $t$에 대해 경계가 모두 0입니다.

시점 $t=0$일 때, 즉 초기일 때, 초기조건은 아래와 같은 모습이죠. $f(x,y)= \sin(\pi x) \sin(\pi y)$라 했을 떄의 모습입니다.

이제 2차원 Heat Equation을 이산화(discretization) 시켜보도록 하죠.
2차원 Heat Eqaution의 이산화
시점 $t=0$부터 $T$까지 분할 간격이 $k$가 되도록 $N$등분합니다. 즉,
$$ 0=t_0<t_1<\cdots <t_{N-1}<t_N =T $$
또, $x,y$는 각각 $I, J$등분하고, 균등 분할 간격이 $h_x, h_y$가 되도록 합니다.
$$ x_{\min} = x_0< x_1 <\cdots < x_{I-1} <x_I =x_{\max} $$
$$ y_{\min} = y_0< y_1 <\cdots < y_{J-1} <y_J =y_{\max} $$
시점 레벨 $n$ 즉 $t=t_n$에서 $(x_i, y_j)$ 에서의 $u$의 값을
$$ u_{ij}^n : = u(t_n, x_i,y_j)$$
라 표현합니다.
무턱대고 해보는 이산화
일단, 함축적 방법(implicit method)을 적용하기 위해 시간에 대한 편미분은 backwardation으로 구해 봅시다.
| 시점 $t_{n+1}$에서 $$ \begin{align} \frac{\partial u}{\partial t} & \approx \frac{u(t_{n+1}-k, x_i,y_j)-u(t_{n+1},x_i,y_j)}{-k}\\ & = \frac{u_{ij}^{n+1} -u_{ij}^n}{k} \end{align} $$ 또한, $$ \begin{align} \frac{\partial^2 u}{\partial x^2} & \approx \frac{u(t_{n+1},x_i+h_x, y_j)-2u(t_{n+1},x_i, y_j)+u(t_{n+1},x_i-h_x, y_j)}{h_x^2}\\ & = \frac{u_{i+1,j}^{n+1}-2u_{ij}^{n+1}+u_{i-1,j}^{n+1}}{h_x^2} \end{align} $$ 이고 마찬가지로 $$\frac{\partial^2 u}{\partial y^2} \approx \frac{u_{i,j+1}^{n+1}-2u_{ij}^{n+1}+u_{i,j-1}^{n+1}}{h_y^2}$$ 입니다. 따라서, $$\frac{u_{ij}^{n+1} -u_{ij}^n}{k} = \frac{u_{i+1,j}^{n+1}-2u_{ij}^{n+1}+u_{i-1,j}^{n+1}}{h_x^2} +\frac{u_{i,j+1}^{n+1}-2u_{ij}^{n+1}+u_{i,j-1}^{n+1}}{h_y^2}$$ |
마지막 식을 보시면, 타임 레벨 $n+1$, 즉 $t=t_{n+1}$에서의 $u$의 값 7개가 time level $n$에서의 값 하나를 결정하는 구조입니다. 전의 글에서는 time level $n$에서의 값 3개가 time level $n+1$에서의 값을 결정했는데 말이죠, 그만큼 관계식이 복잡해지고, 관계식에 등장하는 행렬도 복잡해집니다. 1차원 함축적 방법론(implicit method) 보다 극히 어려워지죠,
복잡성을 타파하기 위해 아래의 방법론을 소개합니다. 이른바
연산분리법(Operator Splitting Mehod)
OSM, Operator Splitting Method
말 그대로 연산을 나누는 방법입니다. Heat Equation의 풀이에서는 $x$에 대한 연산과 $y$에 대한 연산을 나눠서 진행하는 것을 뜻합니다.
time level $n$과 $n+1$사이에, 가상의 시점 $n+\textstyle{\frac12}$를 생각하는 것을 필두로 이론을 진행합니다. 아래 그림을 보시죠.
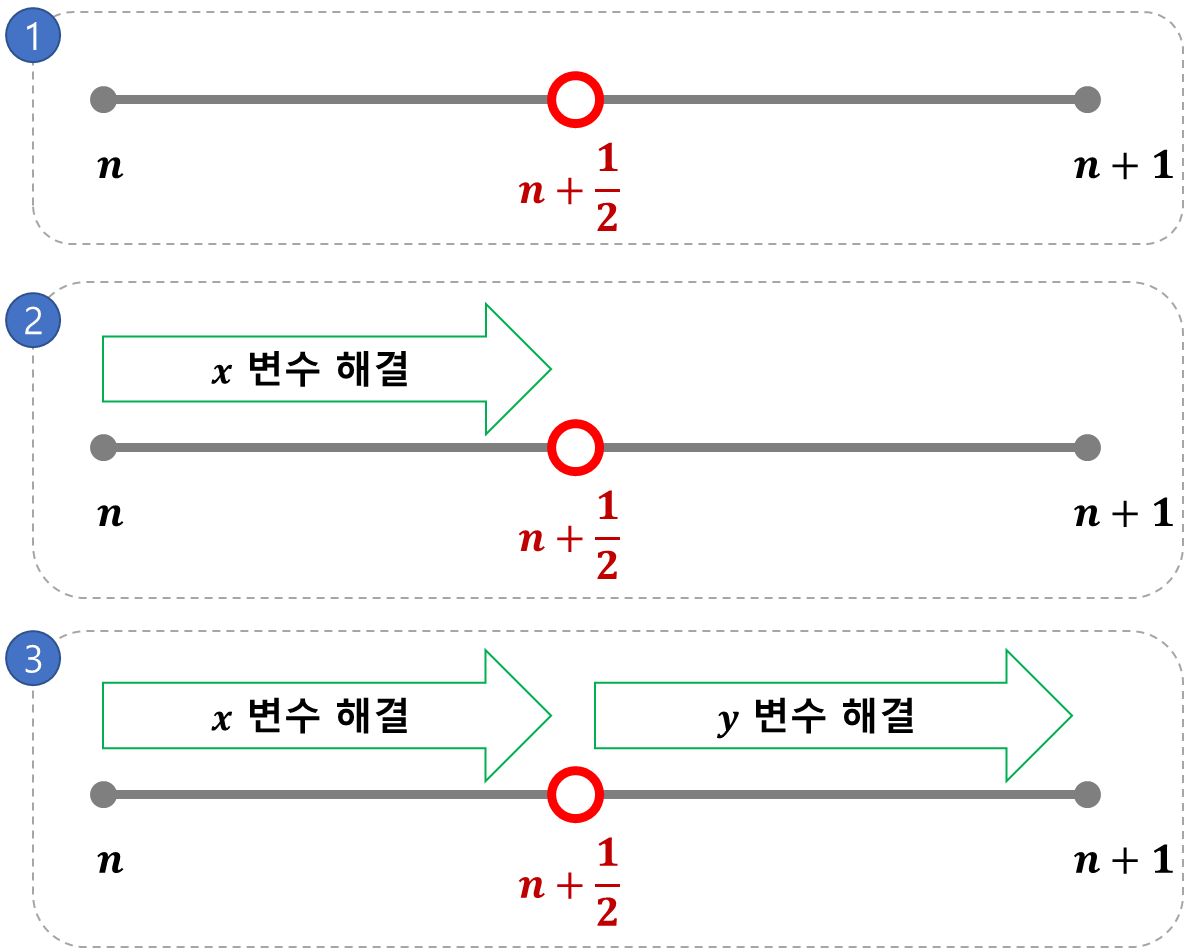
$n$부터 $n+1$ time level까지의 시간을 반으로 나누어 $x$ 변수 먼저 해결하고, 그다음 $y$변수를 해결합니다.
이 절차를 정리해서 써보면 다음과 같습니다.
OSM FDM 해결 절차
위의 내용을 정리해 볼까요?
① $n$과 $n+\textstyle{\frac12}$ 사이에서
$$\frac{u_{ij}^{n+\frac12} -u_{ij}^n}{k} = \frac{u_{i+1,j}^{n+\frac12}-2u_{ij}^{n+\frac12}+u_{i-1,j}^{n+\frac12}}{h_x^2}$$
를 푼다.
② $n+\textstyle{\frac12}$ 과 $n+1$ 사이에서
$$\frac{u_{ij}^{n+1} -u_{ij}^{n+\frac12}}{k} = \frac{u_{i,j+1}^{n+1}-2u_{ij}^{n+1}+u_{i,j-1}^{n+1}}{h_y^2}$$
을 풀어 완성한다.
그러면 ①식은 $x$ 만에 대한 식, ②식은 $y$만의 식이 되어 기존의 implicit method를 사용할 수 있습니다. 이 둘은 저번 글 에서 이미 풀어봤던 식입니다.
Implicit method와 Thomas Algorithm을 써서 풀었죠.
푸는 절차는
$$ u_{ij}^{n} \longrightarrow u_{ij}^{n+\textstyle{\frac12}} \longrightarrow u_{ij}^{n+1}$$
입니다.
수학적인 표현
위 절차를 수학적으로 멋있게 써보면 아래와 같습니다.
차분연산자 $\mathcal{L}^x~,~\mathcal{L}^y$를 각각
$$
\begin{align}
\mathcal{L}^x u_{ij}^{n+\frac12} &= \frac{u_{i+1,j}^{n+\frac12}-2u_{ij}^{n+\frac12}+u_{i-1,j}^{n+\frac12}}{h_x^2}\\
\mathcal{L}^y u_{ij}^{n+1} &= \frac{u_{i,,j+1}^{n+1}-2u_{ij}^{n+1}+u_{i,j-1}^{n+1}}{h_x^2}\\
\end{align}
$$
라 하면
$$\frac{u_{ij}^{n+1}-u_{ij}^n}{k} = \mathcal{L}^x u_{ij}^{n+\frac12} + \mathcal{L}^y u_{ij}^{n+1} $$
입니다.
다음 글에서는 2차원 Heat Equation의 예를 들어, OSM 으로 코딩을 해보도록 하겠습니다.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| 2차원 Heat Equation의 풀이 #3 : OSM 예제풀이2 (0) | 2023.02.13 |
|---|---|
| 2차원 Heat Equation의 풀이 #2 : OSM 예제풀이 (0) | 2023.02.09 |
| FDM #10, Laplace Equation의 풀이(2) Python Code (0) | 2023.02.02 |
| FDM #9, Laplace Equation의 풀이(1) (0) | 2023.02.02 |
| FDM #8, Wave Equation(파동방정식)의 풀이(1) (0) | 2023.01.27 |




댓글