이번 글에서는, 지난 글
2023.02.02 - [수학의 재미/아름다운 이론] - FDM #9, Laplace Equation의 풀이(1)
FDM #9, Laplace Equation의 풀이(1)
지난 글 2023.01.27 - [수학의 재미/아름다운 이론] - FDM #8, Wave Equation(파동방정식)의 풀이(1) FDM #8, Wave Equation(파동방정식)의 풀이(1) 이 글은 FDM #7, Heat Equation의 풀이(3) FDM #7, Heat Equation의 풀이(3) 이
sine-qua-none.tistory.com
에서 알아본 Laplace Equation의 FDM 풀이법을 실제 예제를 들어 python coding으로 풀어보겠습니다.
Laplace Equation 과 FDM풀이법 복습
2 변수 함수 $u(x, y)~,~0\leq x\leq a, 0\leq y \leq b $가 다음의 관계식과 경계조건
$$ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0~~,~~ 0\leq x\leq a, 0\leq y \leq b \tag{L.E.}$$
$$
\begin{align}
u(0,y)&=0 \tag{BC1}\\
u(a,y)&=0 \tag{BC2}\\
u(x,0)&=0 \tag{BC3}\\
u(x,b)&=f(x) \tag{BC4}
\end{align}
$$
을 만족할 때, 이를 Laplace Equation이라 불렀습니다. 이를
$$0=x_0<x_1<x_2<\cdots<x_J =a~~,~~ 0= y_0<y_1<y_2<\cdots <x_K = b$$
로 $x,y$축을 각각 분할 간격 $h_x, h_y$로 균등분할하고 편의를 위해 $h_x=h_y$라 두면
$$ u_{j,k} = \frac{1}{4} \left(u_{j+1,k}+u_{j-1,k} + u_{j,k+1}+u_{j,k-1} \right)$$
를 만족한다고 하였습니다. 또 여기에 Jacobi Iteration 기법을 도입하여 $n$번째 결과를 $u_{j,k}^{(n)}$이라 했을 때, 다음의 절차를 따라 값을 얻을 수 있다고 하였습니다.
FDM 절차
1. $u_{j,k}~,~ 1\leq j\leq J, 1\leq k \leq K$를 초기화한다(예를 들어 모든 값을 0이라 놓는다.)
2. $u_{0,k} =0 ~,~ u_{J,k}=0~, u_{j,0} = 0, u_{j,K}=f(x_j)$ 같이 끝 격자들에 경계조건을 대입!
3. 새로운 격자판 $u_{j,k}^{(2)}$를 만들고, 이 경계조건은 2번과 똑같이 한다.
4. 아래 식을 이용하여 $u_{j,k}^{(2)}$의 값들을 모두 결정해 준다.
$$ u_{j,k}^{(2)} = \frac{1}{4} \left(u_{j+1,k}+u_{j-1,k} + u_{j,k+1}+u_{j,k-1} \right)$$
5. 이제 $u_{j,k}^{(2)}$를 기준으로 하고 위의 1-4 번을 반복하여 $u_{j,k}^{(3)}$ 값들을 만든다.
6. 반복적으로 $u_{j,k}^{(4)}, u_{j,k}^{(5)} ,\cdots$ 를 만들 수 있다.
7. 어떤 허용치(tolerance)를 설정하여 $u_{j,k}^{n}$과 $u_{j,k}^{(n+1)}$의 값이 허용치 안에서 비슷하도록 하는, 즉 더 이상 값이 유의미하게 변하지 않는 상태를 찾으면 끝!
또, 7번의 관계식은 수학적으로
$$ u_{j,k}^{(n+1)} = \frac{1}{4} \left(u_{j+1,k}^{(n)}+u_{j-1,k}^{(n)} + u_{j,k+1}^{(n)}+u_{j,k-1}^{(n)} \right)$$
이고 종국에는 이 값이 거의 변화하지 않는 단계로 수렴한다는 설명을 하였습니다.
Laplace Equation 의 예시
다음의 예시를 풀어보죠.
$$ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0~~,~~ 0 < x< a, 0 < y < b,$$
$$\begin{align}u(0,y)&=0 \\u(a,y)&=0 \\u(x,0)&=0 \\u(x,b)&=c\sin \left( \frac{\pi}{a}x \right)\end{align}$$
위의 예시에서 $a,b,c$는 상수(constant)입니다.
위 함수의 실제 해는 다음과 같습니다(해가 맞는지는 간단한 계산을 통해 알 수 있습니다.)
$$ \frac{c}{\sinh(b\pi/a)} \sin ( \pi x/a) \sinh(\pi y/a) $$
Python Code
def Solve_LaplaceEquation():
# -----------------------------------------------------------------
# u_{xx} + u_{yy} =0 for all 0<x<a and 0<y<b
# u(0,y) = 0
# u(x,0) = 0
# u(a,y) = 0
# u(x,b) = c sin(π/a)x
#
# solution : (c/sinh(π/a *b)) * sin( π * x/a) * sinh(π *y/a)
# -----------------------------------------------------------------
a, b, c = 1, 1, 1 # a,b,c 에 1 대입
xMax = a # x 는 [0,a]
yMax = b # y 는 [0,b]
dl = 0.01 # 분할간격은 0.01
xSeq = np.arange(0, xMax + dl, dl) # [0,a]를 균등분할
ySeq = np.arange(0, yMax + dl, dl) # [0,b]를 균등분할
bdry_function = lambda x: c * np.sin(np.pi / a * x) # y=b 의 boundary function 설정
lx = len(xSeq)
ly = len(ySeq)
u = np.zeros((lx, ly)) # fdm grid 설정
u[0, :] = 0 # x=0일 때의 boundary value
u[-1, :] = 0 # x=a일 때의 boundary value
u[:, 0] = 0 # y=0일 때의 boundary value
u[:, -1] = np.array([bdry_function(x) for x in xSeq]) #y=b일 때 boundary value
u_new = u.copy() # 원본인 u를 건들지 않기 위해 u_new =u 대신, u_new =u.copy()를 써야함
nIteration = 1 # 반복(iteration)의 최대치
tolerance = 0.00001 # u_new와 u 값 사이의 허용오차(tolerance)
error = 100 # error 초기 더미값 (tolerance보다 크기만 하면 됨)
while (nIteration < 100000 and error > tolerance): #최대 10만번 iteration & 허용오차 1/10만
u_new[1: lx - 1, 1: ly - 1] = 0.25 * (u[0:lx - 2, 1:ly - 1] + u[2:lx, 1:ly - 1] +
u[1:lx - 1, 0:ly - 2] + u[1:lx - 1, 2:ly])
# 재귀적 산출 u에서 u_new 로
error = np.linalg.norm(u_new - u) # u와 u_new 사이의 거리(norm)
u = u_new.copy() # u를 다시 u_new값으로 갱신
nIteration += 1
print('Iteration number: {} and error: {}'.format(nIteration,error))
# iteration 횟수와 norm error 출력하여 확인
closed_solution = lambda x, y: c / np.sinh(np.pi / a * b) * np.sin(np.pi * x / a) * np.sinh(np.pi * y / a)
# Laplace equation의 실제 exact formula
for tg_index in range(ly):
# y=y0로 고정하고 u(x, y0) 함수를 x에 대해 그릴 예정
# 위의 y0를 0에서 b까지 for문으로 돌림
u_fixedy = u[:, tg_index] # 해당 y0값의 index 를 tg_index로 하고 이때의 fdm 값
tg_y = ySeq[tg_index] # tg_index 인덱스에 할당된 y값, 즉, y0
cs_fixedy = closed_solution(xSeq, tg_y) #y=y0 에서의 exact solution
plt.plot(xSeq, u_fixedy, color='b', label='fdm')
plt.plot(xSeq, cs_fixedy, color='y', label='exact_solution', linestyle='dashed')
plt.title('At y={:.2f}'.format(tg_y))
plt.legend()
plt.xlabel('x')
plt.ylim([0,1])
plt.pause(0.01) # 0.01초 동안 plotting pause
plt.cla() # graph 지움
plt.show()
if __name__ == '__main__':
Solve_LaplaceEquation()
◆ 코드 중간에 u_new = u.copy() 에 대해 첨언하면, 이것을 u_new = u라고 하면 u_new가 갱신되면서, u 또한 갱신되므로, 즉 배열 타입의 변수가 mutable 한 관계로 같은 주소값을 참조하기에 제대로 된 코드가 될 수 없습니다. 따라서 copy() method를 사용하여 복사를 해주어야 합니다. 관련 내용을 잘 아시는 분의 블로그가 큰 도움이 될 것 같습니다.
◆ numpy.linalg.norm 은 행렬의 다양한 norm을 구해주는 함수입니다. 아무런 옵션도 취하지 않은 default값은 Frobenius norm으로서, 바로 전의 글을 참고해 보시기 바랍니다. 허용오차와 비교하여 u_new와 u사이의 norm값이 작아지면 for문이 멈춥니다.
이제 결과를 보시죠.
Iteration number: 13508 and error: 9.999858290890539e-06
# iteration을 13500번 넘게 해야 허용오차 안에 들어오고, 허용오차는 1/10만인 상태
어떻습니까? 모든 고정된 $y$값에 대해 FDM 값과 실제 closed form 값이 똑같습니다.
(즉 $y$를 고정시키고 $x$에 대한 함수로서 FDM과 closed form을 비교한 결과)
사실 Laplace equation을 만족하는 함수 $u(x,y)$는 2 변수 함수이므로 3차원 공간 안에 그려지는 게 맞을 겁니다. 3D plotting 공부도 할 겸 한번 그려보겠습니다.
def Solve_LaplaceEquation():
# -----------------------------------------------------------------
# u_{xx} + u_{yy} =0 for all 0<x<a and 0<y<b
# u(0,y) = 0
# u(x,0) = 0
# u(a,y) = 0
# u(x,b) = c sin(π/a)x
#
# solution : (c/sinh(π/a *b)) * sin( π * x/a) * sinh(π *y/a)
# -----------------------------------------------------------------
a, b, c = 1, 1, 1
xMax = a
yMax = b
dl = 0.01
xSeq = np.arange(0, xMax + dl, dl)
ySeq = np.arange(0, yMax + dl, dl)
bdry_function = lambda x: c * np.sin(np.pi / a * x)
lx = len(xSeq)
ly = len(ySeq)
u = np.zeros((lx, ly))
u[0, :] = 0
u[-1, :] = 0
u[:, 0] = 0
u[:, -1] = np.array([bdry_function(x) for x in xSeq])
u_new = u.copy()
nIteration = 1
tolerance = 0.00001
error = 100
while (nIteration < 100000 and error > tolerance):
u_new[1: lx - 1, 1: ly - 1] = 0.25 * (u[0:lx - 2, 1:ly - 1] + u[2:lx, 1:ly - 1] +
u[1:lx - 1, 0:ly - 2] + u[1:lx - 1, 2:ly])
error = np.linalg.norm(u_new - u)
u = u_new.copy()
nIteration += 1
print('Iteration number: {} and error: {}'.format(nIteration,error))
closed_solution = lambda x, y: c / np.sinh(np.pi / a * b) * np.sin(np.pi * x / a) * np.sinh(np.pi * y / a)
# 위의 코드는 바로 전 코드와 똑같으므로 설명 생략
#--------------------------------------------------------------------
xval, yval = np.meshgrid(xSeq, ySeq) # x값, y값으로 meshgrid 생성
fig, axs = plt.subplots(ncols=2, figsize=(10, 5), subplot_kw={"projection": "3d"})
# 그래프를 2개 그림, 3d로!
axs[0].plot_surface(xval, yval, u.transpose(), alpha=0.5, color='blue')
# (xval, yval) 점에 함숫값은 u.T의 대응값임
axs[1].plot_surface(xval,yval,closed_solution(xval,yval),alpha=0.5,color='red')
# x= xval, y=yval 에서의 closed form 값
axs[0].view_init(elev=30, azim=120) # 3차원 축의 높이(elevation)와 방위각(azimuth) 조절 기능
axs[1].view_init(elev=30, azim=120)
plt.show()
◆ 3차원 그래프는 축의 각도에 따라 그래프가 잘 보일 수도, 안보일 수도 있기에 view_init 함수로 조절해 줄 수 있습니다. 자세한 내용은 Tutorial을 참고해 보시기 바랍니다. 몇몇 예제는 다음과 같습니다.
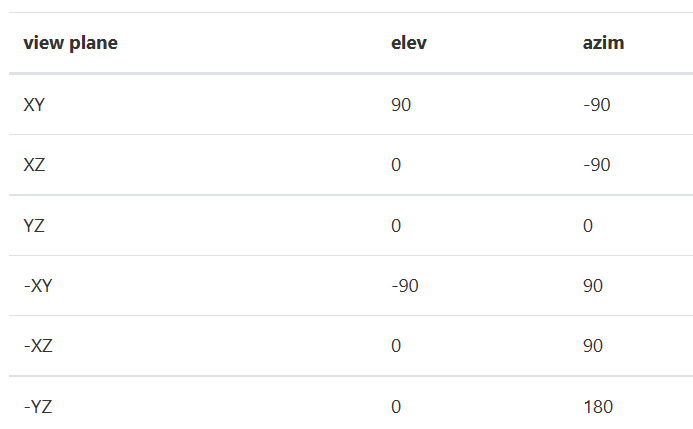
결과를 볼까요?

이번엔 FDM 결과 그래프를 다양한 각도로 조망해 보기 위해 회전을 시켜보도록 하겠습니다.
from matplotlib import animation # 애니메이션 효과를 주기위한 animation import
def Solve_LaplaceEquation():
# -----------------------------------------------------------------
# u_{xx} + u_{yy} =0 for all 0<x<a and 0<y<b
# u(0,y) = 0
# u(x,0) = 0
# u(a,y) = 0
# u(x,b) = c sin(π/a)x
#
# solution : (c/sinh(π/a *b)) * sin( π * x/a) * sinh(π *y/a)
# -----------------------------------------------------------------
a, b, c = 1, 1, 1
xMax = a
yMax = b
dl = 0.01
xSeq = np.arange(0, xMax + dl, dl)
ySeq = np.arange(0, yMax + dl, dl)
bdry_function = lambda x: c * np.sin(np.pi / a * x)
lx = len(xSeq)
ly = len(ySeq)
u = np.zeros((lx, ly))
u[0, :] = 0
u[-1, :] = 0
u[:, 0] = 0
u[:, -1] = np.array([bdry_function(x) for x in xSeq])
u_new = u.copy()
nIteration = 1
tolerance = 0.00001
error = 100
while (nIteration < 100000 and error > tolerance):
u_new[1: lx - 1, 1: ly - 1] = 0.25 * (u[0:lx - 2, 1:ly - 1] + u[2:lx, 1:ly - 1] +
u[1:lx - 1, 0:ly - 2] + u[1:lx - 1, 2:ly])
error = np.linalg.norm(u_new - u)
u = u_new.copy()
nIteration += 1
print('Iteration number: {} and error: {}'.format(nIteration,error))
closed_solution = lambda x, y: c / np.sinh(np.pi / a * b) * np.sin(np.pi * x / a) * np.sinh(np.pi * y / a)
# 위의 코드는 바로 전 코드와 똑같으므로 설명 생략
#--------------------------------------------------------------------
xval, yval = np.meshgrid(xSeq, ySeq)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
def init():
ax.plot_surface(xval, yval, u.transpose(), alpha=0.5, color='blue')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title('Laplace equation')
return fig,
def animate(i):
ax.view_init(elev=30, azim=i) # 30도 각도에서 방위각 i도 만큼 돌리는 animation
return fig,
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=360, interval=20, blit=True)
anim.save('scatter.gif', fps=30)
위 코드에 등장하는 함수들은 FuncAnimation에 관한 Codetorial의 설명이나 전문가분의 블로그를 우선 참고해 주시기 바랍니다. 결과를 gif로 저장가능하며 이때 사용하는 명령하는 save이고 fps를 설정하여 초당 프레임을 설정할 수 있습니다.
결과는 아래와 같습니다.

신기하고도 유용한 기능입니다.
어쨌든 Laplace Equation 역시 FDM으로 해결할 수 있다는 사실을 코드를 통해 알아보았습니다.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| 2차원 Heat Equation의 풀이 #2 : OSM 예제풀이 (0) | 2023.02.09 |
|---|---|
| 2차원 Heat Equation의 풀이 #1 : Operator Splitting Method(OSM) (0) | 2023.02.06 |
| FDM #9, Laplace Equation의 풀이(1) (0) | 2023.02.02 |
| FDM #8, Wave Equation(파동방정식)의 풀이(1) (0) | 2023.01.27 |
| 주성분 분석(PCA) 예제 - 타원 내부 데이터 (0) | 2022.09.11 |




댓글