이번 글은
2022.09.06 - [수학의 재미/아름다운 이론] - 주성분 분석(PCA)의 수학적 접근 #2
주성분 분석(PCA)의 수학적 접근 #2
이번 글은 2022.09.05 - [수학의 재미/아름다운 이론] - 주성분 분석(PCA)의 수학적 접근 주성분 분석(PCA)의 수학적 접근 이번 글은 2022.09.02 - [수학의 재미/아름다운 이론] - 주성분 분석(Principal Componen.
sine-qua-none.tistory.com
에서 이어집니다. 주성분 분석의 수학적 개념에 대해서 알아봤는데, 예제를 통해 직접 분석의 과정을 알아보겠습니다.
좀 작위적인 데이터를 만들어 보겠습니다. 바로 2차원 좌표상의 타원입니다.

주성분 분석은 이 데이터 집합의 주성분 축들을 어떻게 분석해 낼까요? 먼저 데이터 세트를 만드는 방법을 알아보겠습니다.
타원 데이터 세트
타원의 방정식은,
x2a2+y2b2=1
로 주어집니다. a,b>0이고 장축의 길이는 2a, 단축의 길이는 2b입니다. 타원은 매개변수 0≤t≤2π를 사용하여,
x=acost , y=bsint
로 쓸 수 있습니다. 또한 2차원 좌표의 한점 (x,y)를 원점을 기준으로 θ만큼 회전한 좌표를 (X,Y)라 한다면,
(XY)=(cosθ−sinθsinθcosθ)(xy)
의 관계가 성립합니다. 이를 이용하여 원점을 중심으로 회전 이동된 타원 내부에 위치하는 데이터들을 만들어 봅시다.
import numpy as np
import matplotlib.pyplot as plt
def Construct_data():
major_ax, minor_ax = 3, 1
rotation = np.pi / 8
nData = 1000
np.random.seed(0)
rnd_theta = 2 * np.pi * np.random.rand(nData)
rnd_scale = np.random.uniform(-1,1,nData)
x = major_ax * np.cos(rnd_theta)
y = minor_ax * np.sin(rnd_theta)*rnd_scale
xData = np.cos(rotation)*x - np.sin(rotation)*y
yData = np.sin(rotation)*x + np.cos(rotation)*y
plt.scatter(xData, yData, s=10, c='c')
theta_vec = np.linspace(0, 2*np.pi, 100)
ellipse_x = major_ax*np.cos(theta_vec)
ellipse_y = minor_ax*np.sin(theta_vec)
rot_x = np.cos(rotation)*ellipse_x - np.sin(rotation)*ellipse_y
rot_y = np.sin(rotation)*ellipse_x + np.cos(rotation)*ellipse_y
plt.plot(rot_x, rot_y, c='r')
plt.show()
return xData, yData
if __name__ == '__main__':
Construct_data()
간략히 살펴보겠습니다.
major_ax, minor_ax = 3, 1 # 장축의 길이가 2*3, 단축의 길이가 2*1 인 타원을 대상으로 함
rotation = np.pi / 8 # 타원을 원점을 중심으로 pi/8만큼 회전이동한 그림
nData = 1000 # 데이터 샘플의 개수는 1000개를 추출할 예정
np.random.seed(0) # 난수를 발생시킬때마다 달라지지 않게 하기 위해 난수의 seed를 고정함○ 타원 데이터를 가지고 여러 분석을 할 텐데, 실행시킬 때마다 데이터가 달라질 수 있습니다.(난수 발생 과정이 있으므로) 따라서 데이터를 고정시키기 위해 seed 고정을 해줍니다.
# x = a cos(t), y=b sin(t) 로 우선 전형적인 타원 x^2/a^2 + y^2/b^2 =1 위의 점을 추출하여
# y에 [-1,1] 사이의 실수를 곱해줘서 타원 내부의 점을 만들 예정
rnd_theta = 2 * np.pi * np.random.rand(nData) # 매개변수 t를 [0,2pi]사이에서 uniform하게 nData 만큼 추출
rnd_scale = np.random.uniform(-1,1,nData) # y 높이를 조절할 uniform 난수를 [-1,1]사이에서 nData개 추출
x = major_ax * np.cos(rnd_theta)
y = minor_ax * np.sin(rnd_theta)*rnd_scale # y값 조정(타원 내부에 들어오도록)
xData = np.cos(rotation)*x - np.sin(rotation)*y # (x,y)를 rotation 만큼 회전이동한 점의 x좌표
yData = np.sin(rotation)*x + np.cos(rotation)*y # (x,y)를 rotation 만큼 회전이동한 점의 y좌표
plt.scatter(xData, yData, s=10, c='c')
theta_vec = np.linspace(0, 2*np.pi, 100) # [0,2pi] 사이의 균등간격의 theta 설계
ellipse_x = major_ax*np.cos(theta_vec) # 타원의 x좌표
ellipse_y = minor_ax*np.sin(theta_vec) # 타원의 y좌표
rot_x = np.cos(rotation)*ellipse_x - np.sin(rotation)*ellipse_y #(x,y)를 회전이동한 점의 x좌표
rot_y = np.sin(rotation)*ellipse_x + np.cos(rotation)*ellipse_y #(x,y)를 회전이동한 점의 y좌표
plt.plot(rot_x, rot_y, c='r')
return xData, yData #PCA 분석을 위해 타원 내부의 점 (x,y)를 return
결과를 보면,

이처럼 타원(빨간 선) 내부의 점 1000개를 뿌린 데이터를 얻습니다. 데이터의 fetures는 x좌표, y좌표 이렇게 2개이고, 샘플이 1000개 있습니다. 이 데이터 세트를 X라 한다면, X는 1000×2 행렬이 되겠죠.
파이썬을 통한 주성분 분석
Python에서는 주성분 분석(PCA)을 위한 툴을 제공합니다.
주성분 분석을 위해서는 sklearn.decomposition 이라는 모듈 아래 PCA 라는 클래스를 이용하면 편리합니다. 따라서 이를 import 하기 위해
from sklearn.decomposition import PCA를 우선 해 주어야 합니다. 위의 타원 분석을 위한 python code를 보시죠.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
def Construct_data():
# 위와 동일
def pca_simulation():
xdata, ydata = Construct_data()
X = np.vstack((xdata, ydata))
X = X.transpose()
X_mean = X.mean(axis=0)
X -= X_mean
pca = PCA(n_components=2)
pca.fit(X)
new_axis = pca.components_
var = pca.explained_variance_
print('\n\n')
print('1. Principal Component(eigen vector) is \n', new_axis)
print('-' * 30)
print('\n\n')
print('2. Variance(eigen value) is\n', var)
print('-' * 30)
# check eigendecomposition
C = np.cov(X.transpose(), bias=True)
CQ = C @ new_axis.T
D = np.diag(var)
QD = new_axis.T @ D
print('\n\n')
print('3. Check EigenDecomposition\n')
print(' 1) Covariance matrix(C) \n', C)
print('-' * 10)
print(' 2) EigenVectir matrix(Q) \n', new_axis.T)
print('-' * 10)
print(' 3) Diagonal Eigenvalue matrix(D) \n', D)
print('-' * 10)
print(' 4) CQ-QD : \n', CQ - QD)
print('-' * 30)
x0 = X[:1, :] # first original data
first_eigenvector, second_eigenvector = new_axis[0, :], new_axis[1, :] # 첫번째 주성분, 두번째 주성분
transform_x0_x = x0 @ first_eigenvector # 변환 후 첫번째 좌표
transform_x0_y = x0 @ second_eigenvector # 변화 후 두번째 좌표
print('\n\n')
print('4. Check Transforem Result\n')
print(' 1) transform of x0 :\n', np.array([transform_x0_x, transform_x0_y]).reshape(1, 2))
print('-' * 10)
print(' 2) transform of x0(using python method):\n', pca.transform(x0))
print('-' * 30)
first_slope = first_eigenvector[1] / first_eigenvector[0]
second_slope = second_eigenvector[1] / second_eigenvector[0]
print('\n\n')
print('5. Check Principal Component(New axsis)\n')
print(' 1) first_slope, second slope = {}. {}'.format(first_slope, second_slope))
print('-' * 10)
print(' 2) tan(pi/8) = {}'.format(np.tan(np.pi / 8)))
print('-' * 10)
x = np.linspace(-3, 3, 100)
plt.axis('equal')
plt.scatter(xdata, ydata, s=10)
plt.plot(x, x * first_slope, color='r')
plt.plot(x / 3, 1 / 3 * x * second_slope, color='g')
plt.xlim(-3.5, 3.5)
plt.ylim(-3.5, 3.5)
plt.show()
if __name__ == '__main__':
pca_simulation()
간략히 살펴보겠습니다.
xdata, ydata = Construct_data() # pi/8만큼 회전된 타원내부의 x좌표(xdata), y좌표(ydata)
X = np.vstack((xdata, ydata)) # 1*1000 배열 xdata, ydata를 수직으로쌓아(vertical stack) 2*1000행렬 만듬
X = X.transpose() # transpose하여 1000*2행렬 만듬
X_mean = X.mean(axis=0) #axis =0 으로 평균, 즉 각 열의 데이터의 평균을 구함
X -= X_mean # 평균을 각 열에서 빼줌○ xdata를 (x1,x2,⋯,xN), ydata를 (y1,y2,⋅,syN)이라 하면,
○ np.vstack((xdata, ydata)) 는
(x1x2⋯xNy1y2⋯yN)
○ X = X.transpose()하면 X는
X=(x1y1x2y2⋮⋮xNyN)
pca = PCA(n_components=2) # 주성분의 개수(n_components)가 2개인 PCA 분석 class 선언
pca.fit(X) # 데이터 X를 PCA 분석 실시
new_axis = pca.components_ # 주성분 2벡터를 new_axis라 하고
var = pca.explained_variance_ # 각 성분으로의 정사영의 분산이자, eigen value를 var 에 대입
print('\n\n')
print('1. Principal Component(eigen vector) is \n', new_axis) #주성분 출력
print('-' * 30)이것의 결과는 다음과 같습니다.
1. Principal Component(eigen vector) is
[[-0.92569385 -0.37827357]
[-0.37827357 0.92569385]]
------------------------------○ 주성분 벡터가 각각
w1=[−0.92569385,−0.37827357] , w2=[−0.37827357,0.92569385] 입니다.
print('\n\n')
print('2. Variance(eigen value) is\n', var)
print('-' * 30)이것의 결과는
2. Variance(eigen value) is
[4.55815135 0.17993497]
------------------------------입니다. 즉, covariance matrix C를 고윳값 분해했을 때 고윳값 λ1,λ2를 크기 순으로 나열한 벡터를 반환합니다.
# check eigendecomposition
C = np.cov(X.transpose(), bias=True) # X data의 두 feature xdata, ydata 사이의 공분산행렬
CQ = C @ new_axis.T #고윳갑 분해의 좌변
D = np.diag(var) # eigenvalue를 대각원소로 하는 대각행렬 만듬
QD = new_axis.T @ D # 고윳값 분해의 우변
print('\n\n')
print('3. Check EigenDecomposition\n')
print(' 1) Covariance matrix(C) \n', C)
print('-' * 10)
print(' 2) EigenVectir matrix(Q) \n', new_axis.T)
print('-' * 10)
print(' 3) Diagonal Eigenvalue matrix(D) \n', D)
print('-' * 10)
print(' 4) CQ-QD : \n', CQ - QD)
print('-' * 30)이 결과는 아래와 같습니다.
3. Check EigenDecomposition
1) Covariance matrix(C)
[[3.9277368 1.53156729]
[1.53156729 0.80561143]]
----------
2) EigenVectir matrix(Q)
[[-0.92569385 -0.37827357]
[-0.37827357 0.92569385]]
----------
3) Diagonal Eigenvalue matrix(D)
[[4.55815135 0. ]
[0. 0.17993497]]
----------
4) CQ-QD :
[[ 4.21945269e-03 6.80646439e-05]
[ 1.72422816e-03 -1.66564699e-04]]
------------------------------○ X의 공분산 행렬은 numpy.cov 로 만들 수 있습니다. 공분산과 공분산 행렬 글을 참고해 보시기 바랍니다.
○ 공분산행렬 C의 고윳값 분해는
C⋅(∣∣w1w2∣∣)=(∣∣w1w2∣∣)⋅(λ100λ2)
입니다. 이게 만족하는 지를 테스트 한 결과입니다.
○ 4)의 CQ-QD의 결과가 영행렬이 아니고 아주 작은 에러 값들을 보이는 모습이네요.
x0 = X[:1, :] # first original data
first_eigenvector, second_eigenvector = new_axis[0, :], new_axis[1, :] # 첫번째 주성분, 두번째 주성분
transform_x0_x = x0 @ first_eigenvector # 변환 후 첫번째 좌표
transform_x0_y = x0 @ second_eigenvector # 변화 후 두번째 좌표
print('\n\n')
print('4. Check Transforem Result\n')
print(' 1) transform of x0 :\n', np.array([transform_x0_x, transform_x0_y]).reshape(1, 2))
print('-' * 10)
print(' 2) transform of x0(using python method):\n', pca.transform(x0))
print('-' * 30)결과는 다음과 같습니다.
1) transform of x0 :
[[ 2.88317768 -0.0649485 ]]
----------
2) transform of x0(using python method):
[[ 2.88317768 -0.0649485 ]]
------------------------------○ 새로운 주성분 축에 대해 좌표가 어떻게 되는지를 구하는 방법입니다. 수학적으로 벡터 x를 주성분 w 에 정사영시키면 벡터 w에 대한 좌표가 w⋯w임을 소개한 바 있습니다.
○ 주성분이 w1,w2이므로 어떤 점 (x1,y1)을 해당 성분들에 대한 좌표로 표시하면
X=(x1,y1)↦(X⋅w1,X⋅w2) 로 바뀌게 됩니다.
○ python에서는 pca.transform() 함수를 이용하여 쉽게 구할 수 있습니다.
○ 수학적으로 계산한 값과 python 함수의 결괏값이 똑같습니다.
first_slope = first_eigenvector[1] / first_eigenvector[0] # 첫번째 주성분 벡터의 기울기
second_slope = second_eigenvector[1] / second_eigenvector[0] #두번째 주성분 벡터의 기울기
print('\n\n')
print('5. Check Principal Component(New axsis)\n')
print(' 1) first_slope, second slope = {}. {}'.format(first_slope, second_slope))
print('-' * 10)
print(' 2) tan(pi/8) = {}'.format(np.tan(np.pi / 8)))
print('-' * 10)
x = np.linspace(-3, 3, 100)
plt.axis('equal')
plt.scatter(xdata, ydata, s=10)
plt.plot(x, x * first_slope, color='r')
plt.plot(x / 3, 1 / 3 * x * second_slope, color='g')
plt.xlim(-3.5, 3.5)
plt.ylim(-3.5, 3.5)
plt.show()결과를 보시죠.
5. Check Principal Component(New axsis)
1) first_slope, second slope = 0.4086378710619287. -2.447154487667275
----------
2) tan(pi/8) = 0.41421356237309503
----------
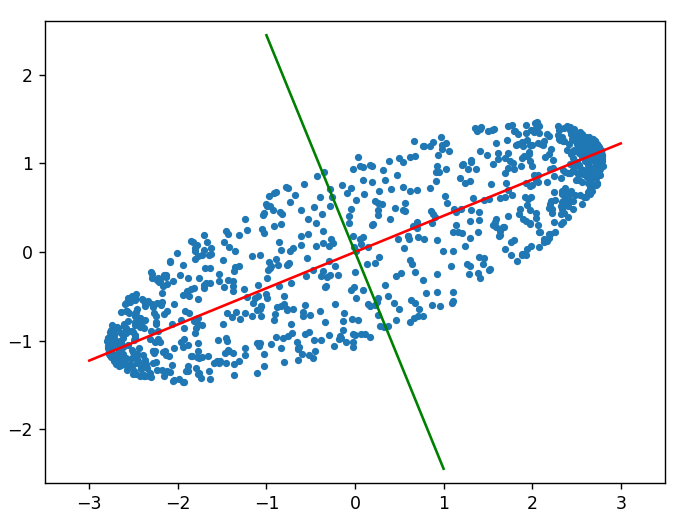
어떻습니까?
장축이 단축보다 긴 타원 데이터를 원점을 중심으로 π8만큼 회전시켜 얻은 데이터의 주성분 분석을 했더니 주성분의 기울기가 0.4086 정도 나왔는데요, 이는 신기하게도(또는 당연히!) tan(π/8)의 값과 거의 같습니다. 회전 변환하기 전의 데이터들 분산이 가장 큰 방향은 직관적으로 x축 즉 (1,0) 방향이 주성분일 거고, 회전 변환에 의해 축도 같이 회전 변환하여 위 그림의 빨간 축이 됩니다.
○ 여담으로, python의 plotting 기술 하나를 소개하자면,
plt.axis('equal')이라는 명령어가 있습니다. 이는 plotting 영역의 x축, y축의 종횡비를 똑같게 만들어주는 것입니다. 시각적으로 위 그림의 빨간색, 녹색 주성분들이 직교함을 보이기 위해서 종횡비를 1로 설정할 필요가 있는데, 그때 적용하는 명령어입니다.
사실, 위 타원 데이터를 좀 작위적인 데이터라, 결과가 쉽게 예측이 되고 그 결과대로 답이 나옵니다. 복잡한 데이터에 대한 분석에서는 이렇게 직관적으로 와닿지는 않겠죠. 앞으로 PCA 분석을 해 볼 만한 좋은 예제를 발굴하여 다시 주성분 분석을 심도 있게 파헤쳐보도록 하겠습니다.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| FDM #9, Laplace Equation의 풀이(1) (0) | 2023.02.02 |
|---|---|
| FDM #8, Wave Equation(파동방정식)의 풀이(1) (0) | 2023.01.27 |
| 주성분 분석(PCA)의 수학적 접근 #2 (2) | 2022.09.06 |
| 주성분 분석(PCA)의 수학적 접근 (0) | 2022.09.05 |
| 주성분 분석(Principal Component Analysis)이란? (2) | 2022.09.02 |




댓글