이번 글은
2022.09.02 - [수학의 재미/아름다운 이론] - 주성분 분석(Principal Component Analysis)이란?
주성분 분석(Principal Component Analysis)이란?
이 글에서 다룰 내용은 주성분 분석(principal component analysis, PCA) 기법입니다. 주성분 분석이란 간단히 말해 주성분 분석 고차원의 데이터를 저 차원의 데이터로 축소시켜 분석하기 위해 쓰는 기법
sine-qua-none.tistory.com
에서 이어집니다. 지난 글에서는 주성분 분석의 개념과 주성분 분석을 가지고 무엇을 하려는지를 설명했는데요, 그렇다면 저번 글에서 말한 "데이터를 잘 설명할 수 있는 축"들을 어떻게 찾는지를 알아보겠습니다.
먼저 수학적으로 세팅을 해보겠습니다.
수학적 세팅
데이터 각각의 feature는 $p$개
데이터마다 feature(특징)을 $p$개 씩 가지고 있다고 합시다. 이 feature들은 모두 숫자로 표현되며, 데이터 $\mathbf{x}$의 feature들을 각각 $x_1, x_2, \cdots, x_p$라 할 때,
$$ \mathbf{x} = (x_1, x_2,\cdots, x_p)$$
로 표현된 $\mathbf{x} \in \mathbb{R}^p$ 라고 생각할 수 있습니다.
데이터 샘플(표본), 즉 관찰된 데이터의 개수는 $N$개
feature를 각각 $p$개 가진 데이터들을
$$\mathbf{x}_1 , \mathbf{x}_2, \cdots, \mathbf{x}_N$$
처럼 $N$개를 모았다고 가정하겠습니다. 위 각각의 데이터 $\mathbf{x}_i$는 원소를 $p$개 가진 $\mathbf{R}^p$상의 벡터라고 생각할 수 있고, 첨자를 조금 구체적으로 써서
$$\mathbb{x}_i = (x_{i1}, x_{i2}, \cdots, x_{ip})$$
라 쓸 수 있습니다.
데이터 샘플의 평균은 $\mathbf{0}$
$$\mathbf{x}_1 , \mathbf{x}_2, \cdots, \mathbf{x}_N$$ 의 평균을 $\mathbf{0}$이라 가정할 수 있습니다.
만일 평균이 $\mathbf{0}$이 아니면,
$$ \frac1N \sum_{i=1}^N \mathbf{x_i} =(\mu_1,\mu_2,\cdots,\mu_p) :=\mathbf{\mu}$$
로 주어질 텐데, 다시 데이터 샘플을
$$\mathbf{x}_1-\mathbf{\mu} , \mathbf{x}_2- \mathbf{\mu}, \cdots, \mathbf{x}_N-\mathbf{\mu}$$
라 생각하면 되기 때문이죠. 평균만큼 평행 이동하여 조정해준 새로운 데이터 샘플을 평균이 $\mathbf{0}$이 나오게 됩니다.
위의 데이터로 행렬 만들기
각각의 데이터 샘플이 행이 되도록 하는 $N\times p$ 행렬 $\mathbf{X}$를 만듭니다. 즉,
$$
\mathbf{X}=
\begin{pmatrix}
\rule[.2ex]{1em}{0.2pt} & \mathbf{x_1} & \rule[.2ex]{1em}{0.2pt} \\
\rule[.2ex]{1em}{0.2pt} & \mathbf{x_2} & \rule[.2ex]{1em}{0.2pt} \\
& \vdots & \\
\rule[.2ex]{1em}{0.2pt} & \mathbf{x_N} & \rule[.2ex]{1em}{0.2pt} \\
\end{pmatrix}
=
\begin{pmatrix}
x_{11} & x_{12} & \cdots &x_{1p} \\
x_{21} & x_{22} & \cdots &x_{2p} \\
\vdots & \vdots & \ddots &\vdots \\
x_{N1} & x_{N2} & \cdots &x_{Np} \\
\end{pmatrix} \tag{1}
$$
입니다.
이제 수학적으로 정사영(projection)이 무엇인지 한번 알아보도록 하겠습니다.
정사영(projection)
벡터 $\mathbf{x}$를 벡터 $\mathbf{w}$로 정사영시키는 문제입니다.
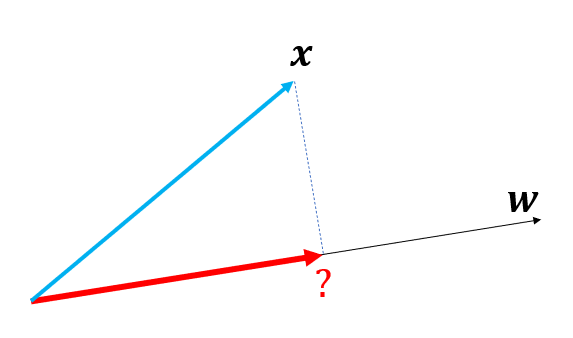
정사영은 $\mathbf{x}$벡터를 $\mathbf{w}$에 수직으로 내렸을 때, 빨간색 벡터를 어떻게 표시할 수 있냐는 것입니다.
빨간색 벡터는 $\mathbf{w}$와 평행하므로 상수 $k$가 있어서
$$ k\mathbf{w}$$
라 쓸 수 있죠. 이제 $k$를 구해봅시다.

이런 상황이므로 $\mathbf{x}-k\mathbf{w}$와 $\mathbf{w}$는 수직이죠. 따라서
$$ \mathbf{w} \cdot(\mathbf{x}-k\mathbf{w})=0$$
입니다( $\cdot$ 기호는 내적입니다.)
이것을 풀면
$$ k = \frac{\mathbf{x\cdot w}}{\| \mathbf{w} \|^2}$$ 이죠. $\| \|$ 기호는 norm으로서 $\|\mathbf{a}\|^2 =\mathbf{ a\cdot a}$를 뜻하고 이는 벡터 $\mathbf{a}$의 길이입니다.
따라서 다음의 결론을 얻습니다.
임의의 벡터 $\mathbf{x}$를 크기가 1인 벡터 $\mathbf{w}$로 정사영한 벡터는
$$(\mathbf{x\cdot w})\mathbf{w}$$
이다.
잔차(Residual) 분석
잔차라는 개념은 벡터 $\mathbf{x}$가 $\mathbf{w}$와 떨어져 있는 거리입니다. 벡터 $\mathbf{x}$를 $\mathbf{w}$에 가깝게 표시하고 싶은데 차이가 나죠. 그 차이를 잔차라고 합니다. 그림으로 보면,

입니다. 잔차를 의미하는 벡터는
$$\mathbf{x}-\mathbf{(x\cdot w)w}$$
이고 따라서 이 잔차의 제곱은
$$ \|\mathbf{x}-\mathbf{(x\cdot w)w}\|^2$$
이지요.
이제 수학적 세팅에서 다루었던 대로, 샘플 벡터가 $N$개 있다고 합시다. 즉
$\mathbf{x_1, x_2 ,\cdots, x_N}$은 feature가 $p$개인 $\mathbb{R}^p$의 벡터가 샘플로 주어진 상황입니다. 더군다나, 이 들의 평균은 $\mathbf{0}$인 상황입니다.

잔차 제곱의 합을 계산해 보죠. 잔차제곱의 합은
$$\sum_{i=1}^N \| \mathbf{x_i - (x_i\cdot w)w}\|^2$$
로 주어집니다. 이것을 기호로 $RSS(\mathbf{w})$라 써보겠습니다. 그러면
$$
\begin{align}
RSS(\mathbf{w}) & = \sum_{i=1}^N \| \mathbf{x_i - (x_i\cdot w)w}\|^2\\
& = \sum_{i=1}^N \|\mathbf{x_i}\|^2 - 2(\mathbf{x_i\cdot w})^2 + \mathbf{(x_i\cdot w})^2\|\mathbf{w}\|^2 \\
& = \sum_{i=1}^N \|\mathbf{x_i}\|^2 - (\mathbf{x_i\cdot w})^2~~(\because \|\mathbf{w}\|=1) \tag{2}
\end{align}
$$
입니다.
잔차 제곱의 합이 최소가 되려면..
이제, 우리의 목적은 잔차 제곱의 합이 최소가 되는 벡터 $\mathbf{w}$를 찾는 것입니다. 왜일까요? 지금 우리가 가지고 있는 샘플 $\mathbf{x_1, \cdots, x_N}$ 을 대표 벡터 하나로 설명하고 싶은 겁니다. 그러려면, 이 샘플들과 거리가 최소로 떨어진 축을 하나 찾아야겠죠(마치 선형 회귀와 비슷합니다.)
즉, $RSS(\mathbf{w})$를 최소로 하는 길이가 1인 벡터 $\mathbf{w}$을 찾는데 목적이 있습니다.
좀 더 분석을 해보죠. 식(2)에 의하면
$$ RSS(\mathbf{w}) =\sum_{i=1}^N \|\mathbf{x_i}\|^2 - (\mathbf{x_i\cdot w})^2 $$
입니다. 그런데 $\sum_{i=1}^N \|\mathbf{x_i}\|^2$은 고정된 상수이죠. 왜냐면 샘플은 이미 주어진 상태이니까요.
따라서
$RSS(\mathbf{w}) $ 가 최소라는 얘기는
$$ \sum_{i=1}^N (\mathbf{x_i\cdot w})^2 \tag{3} $$
가 최대가 되는 길이 1인 벡터 $\mathbf{w}$를 구하는 문제라는 이야기입니다.
위 문제를 행렬의 언어로 바꿔 생각하기
바로 위 문제를 행렬의 언어로 바꿔보겠습니다. 식(3)이 최대라는 얘기는
$$ \frac1N \sum_{i=1}^N (\mathbf{x_i\cdot w})^2 \tag{4}$$
가 최대라는 얘기와 동치입니다. $N$은 상수이기 때문이죠.
관점을 돌려서, 식(1)에서 정의한 행렬 $\mathbf{X}$를 떠올려 보죠.
$$ \mathbf{Xw} = \begin{pmatrix} \mathbf{x_1 w} \\ \mathbf{x_2 w} \\ \vdots \\ \mathbf{x_N w} \end{pmatrix} $$
입니다. 따라서
$$ \sum_{i=1}^N (\mathbf{x_i\cdot w})^2 = (\mathbf{Xw})^t \mathbf{Xw} $$ 이죠. $\|a\|^2 = a^t a$ 을 이용했습니다.
따라서
$$
\begin{align}
(4) & =\frac1N \sum_{i=1}^N (\mathbf{x_i\cdot w})^2 \\
& = \frac1N (\mathbf{Xw})^t \mathbf{Xw} \\
& = \frac1N \mathbf{w^t X^tX w} \\
& =\mathbf{w}^t \left( \frac1N \mathbf{X^t X} \right) \mathbf{w} \\
& :=\mathbf{ w^t C w}
\end{align}
$$
입니다.
과연 $ \mathbf{C} = \frac1N \mathbf{X^t X} $로 정의된 이 행렬, 무엇일까요? 바로
$X$의 공분산 행렬(covariance matrix)
입니다. 지난 글 공분산과 공분산 행렬에서 다루었습니다. 따라서 이제 우리는 명확한 목적을 얻게 됩니다.
GOAL:
Features가 $p$개인 데이터 샘플 $X_1, X_2, \cdots, X_N$ 이 있다고 했을 때,
$$ \mathbf{w^t C w}$$
를 최대로 하는 길이 1인 $\mathbb{R}^p$ 벡터 $\mathbf{w}$는 어떻게 구할 수 있나?
여기서 $\mathbf{C}$는 $X$의 $p \times p$ 공분산 행렬(covariance matrix)이다.
이 문제를 푸는 방법은 다음 글에서 하겠습니다.
여담
지난 글 주성분 분석(Principal Component Analysis)이란? 에서 주성분 분석은
1. 첫 번째 축을 찾는다.
어떻게 찾냐면, 데이터들을 이 축에 떨어뜨려(사영, projection) 봤을 때 분산이 가장 커지는 방향의 축을 찾는다.
2. 두 번째 축을 찾는다.
첫 번째 축과 수직인 축들 중에서, 데이터들을 이 축에 떨어뜨려 봤을 때 분산이 가장 커지는 방향 축을 찾는다.
3. 이런 식으로 원하는 만큼의 축을 찾는다.
라고 얘기했습니다. 그런데 이 글에서 분산 얘기가 하나도 안 나왔죠. 이번 글에서 알아본 방법이 분산과 관련이 있을까요?
식(4)을 보면
$$ \frac1N \sum_{i=1}^N (\mathbf{x_i\cdot w})^2$$
가 최대인 $\mathbf{w}$를 찾는 것이 주성분 분석의 목표라 했습니다.
$$ y_i = \mathbf{x_i \cdot w},~~ i=1,2,\cdots,N $$
라 두어 본다면, 식 (4)는
$$ \mathbb{E}(y_i^2) $$입니다.
그런데
$$
\begin{align}
\mathbb{E}(y_i) & = \frac1N \sum_{i=1}^N y_i \\
& = \frac1N \sum_{i=1}^N \mathbf{x_i\cdot w} \\
& = \left( \frac1N \sum_{i=1}^N \mathbf{x_i} \right) \cdot \mathbf{w} \\
& =0
\end{align}
$$
입니다. 왜냐면 $\mathbf{x_i}$들의 평균을 $\mathbf{0}$ 이라 했기 때문이죠.
따라서
$$ \mathbb{E}(y_i^2) = \mathbb{E}(y_i)^2 +\mathbb{V}(y_i) = \mathbb{V}(y_i)$$
가 되므로
$ \mathbb{E}(y_i^2)$ 를 최대로 한다는 뜻은 $\mathbb{V}(y_i)$ 를 최대로 한다는 뜻입니다.
또 $y_i$들은
$$ \mathbf{x_i} = y_i \mathbf{w}$$
를 만족하는 값으로서 $\mathbf{w}$ 방향 축으로의 좌표가 됩니다($\mathbf{w}$의 크기가 1이므로)

$y_i$들은 $\mathbf{x_i}$를 $\mathbf{w}$로 떨어뜨린 지점의 좌표를 얘기하는 것이고 따라서, 이 좌표들의 분산이 제일 커지도록 $\mathbf{w}$를 찾자는 얘기가 되는 것이죠.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| 주성분 분석(PCA) 예제 - 타원 내부 데이터 (0) | 2022.09.11 |
|---|---|
| 주성분 분석(PCA)의 수학적 접근 #2 (2) | 2022.09.06 |
| 주성분 분석(Principal Component Analysis)이란? (2) | 2022.09.02 |
| FDM #7, Heat Equation의 풀이(3) (0) | 2022.08.01 |
| FDM #6, Heat Equation의 풀이(2) (0) | 2022.08.01 |




댓글