이번 글은
2022.09.05 - [수학의 재미/아름다운 이론] - 주성분 분석(PCA)의 수학적 접근
주성분 분석(PCA)의 수학적 접근
이번 글은 2022.09.02 - [수학의 재미/아름다운 이론] - 주성분 분석(Principal Component Analysis)이란? 주성분 분석(Principal Component Analysis)이란? 이 글에서 다룰 내용은 주성분 분석(principal compone..
sine-qua-none.tistory.com
에서 이어집니다.
지난 글에서, 주성분 분석은 주어진 샘플 데이터들의 잔차를 최소화, 다른 말로 분산을 최대화하는 축을 찾는 문제라는 거을 얘기했습니다.
주성분 분석의 수학적 목표
GOAL:
Features가 $p$개인 데이터 샘플 $X_1, X_2, \cdots, X_N$ 이 있다고 했을 때,
$$ \mathbf{w^t C w}$$
를 최대로 하는 길이 1인 $\mathbb{R}^p$ 벡터 $\mathbf{w}$는 어떻게 구할 수 있나?
여기서 $\mathbf{C}$는 $X$의 $p \times p$ 공분산 행렬(covariance matrix)이다.
한 가지 가정: 샘플 데이터 $X_i$들의 평균은 0이다.
입니다.
이 문제를 풀기 위해서는 라그랑즈 승수법(Lagrage multiplier)라는 수학적 방법을 알아야 합니다.
라그랑주 승수법
원래 라그랑즈 승수법은 조금 더 복잡하지만, 이 상황을 해결하는데 맞게끔 한번 써보겠습니다.
라그랑주 승수법(Lagrange Multiplier)
미분가능한 다변수 함수 $f:\mathbb{R}^p \rightarrow \mathbb{R}$과 $g:\mathbb{R}^p \rightarrow \mathbb{R}$가 있다고 하자. 어떤 상수 $c$에 대해, $f$가 집합 $S=\{ \mathbf{x}\in \mathbb{R}^p | g(\mathbf{x}) =c\}$ 에서 극점 $\mathbf{x}^\ast \in \mathbb{R}^p$를 가진다면 $\nabla f(\mathbf{x}^\ast)$와 $\nabla g(\mathbf{x}^\ast)$가 1차 종속이다. 다시 쓰면,
$$ \nabla f(\mathbf{x}^\ast ) = \lambda \nabla g(\mathbf{x}^\ast) $$
인 $\lambda$가 존재한다.
조금 어렵지요? 우리의 GOAL을 여기에 맞춰 써보겠습니다.
주성분 분석의 최적화 문제
라그랑즈 승수법을 염두에 두고 주성분 분석의 목적을 써본다면, 아래와 같이 정리할 수 있습니다.
GOAL
○ 목적함수(objective function)
$$ f: \mathbb{R}^p \rightarrow \mathbb{R}, \mathbf{w} \mapsto \mathbf{w^t C w} $$
○ 제약함수(constraint function)
$$ g: \mathbb{R}^p \rightarrow \mathbb{R} , \mathbf{w} \mapsto \mathbf{w^t w} $$
라 하면 $f$ 함수의 극점을 $\{ \mathbf{w}\in\mathbb{R}^p | g(\mathbf{w}) = 1\}$ 위에서 찾는 문제임
차근차근 계산해 보겠습니다.
$f$의 그래디언트 $\nabla f$
$\mathbf{w} = (w_1, w_2,\cdots, w_p)$ 라 하고 $\mathbf{C} = \{ C_{ij}\}$ 라 합시다.
그러면
$$ \mathbf{w^t C w} = \sum_{i=1}^p C_{ii} w_i^2 + 2\sum_{i<j} C_{ij}w_i w_j $$
입니다.
따라서 첨자 $k$에 대해,
$$\frac{\partial f}{\partial w_k} = 2C_{kk} w_k + 2 \sum_{i=1, i\neq k}^p C_{ik} w_i =2 \sum_{i=1}^p C_{ki} w_i $$
입니다.
이것을 종합해보면,
$$\nabla f(\mathbf{w}) = 2\mathbf{C w}$$
입니다.
$g$의 그래디언트 $\nabla g$
$$ g(\mathbf{w}) = \mathbf{w^t w} = w_1^2 + w_2^2 +\cdots +w_p^2 $$
입니다. 따라서 첨자 $k$에 대해
$$\frac{\partial g}{\partial w_k} = 2w_k$$
이죠. 따라서
$$\nabla g(\mathbf{w}) = 2\mathbf{w}$$
입니다.
이제, 라그랑즈 승수법을 적용해 보겠습니다.
$f$를 최대로 만드는 $\mathbf{w^\ast}$는
$$ 2\mathbf{Cw^\ast} = \lambda 2\mathbf{w^\ast} \tag{1}$$
의 등식이 만족하는 실수 $\lambda$가 있습니다. 식(1)을 정리하면
$$ \mathbf{Cw} = \lambda \mathbf{w} \tag{2}$$
를 만족하는 $\mathbf{w}$가 바로 우리가 찾는 그 값일 것입니다. 그렇다면 식(2)에서 어떻게 $\lambda$와 벡터 $\mathbf{w}$를 찾을 수 있을까요?
고유값 분해
2022.06.03 - [수학의 재미/행렬 이론] - 고유값 분해(eigen decomposition) #1
고유값 분해(eigen decomposition) #1
2차원 땅이나 3차원 공간에서 물체의 움직임이나 현상의 변화를 설명할 때, 행렬이 많이 쓰입니다. 또는 숫자의 배열로서 행렬이 쓰이는데, 분석을 쉽게, 또 간단히 하기 위해 주어진 행렬을 더
sine-qua-none.tistory.com
에서 고윳값 분해(eigen decomposition)을 다룬 적이 있습니다. $n \times n$ 정사각행렬 $\mathbf{A}$의 고윳값, 고유 벡터 pair를 $(\lambda_i, \mathbf{v_i}), i=1,2,\cdots, n$이라 하고
○ $\mathbf{v_i}$를 열 벡터로 하는 행렬을 $\mathbf{Q}$,
○ $\lambda_i$를 대각 원소로 하는 대각 행렬을 $\mathbf{D}$
라 했을 때,
$$\mathbf{AQ} = \mathbf{QD}$$
가 성립합니다(이 단계까지는 고윳값은 복소수까지 허용되고, $\mathbf{Q}$는 가역 행렬이 아닐 수도 있습니다.)
한 단계 더 나아가서,
2022.07.02 - [수학의 재미/행렬 이론] - 대칭행렬 만들고 고윳값 분해하기 에서는 만일 행렬 $\mathbf{A}$가 대칭행렬이면,
○ 고윳값 $\lambda_i$ 들은 실수이고,
○ 고유벡터 $\mathbf{v_i}$들은 서로 직교(orthogonal)하기 때문에 이들을 열 벡터로 하는 $\mathbf{Q}$는 직교행렬이 되고 자동으로 가역행렬이 됩니다.
한 단계 더 나가볼까요? 만일 행렬 $\mathbf{A}$가 positive definite 라 합시다.
2022.07.04 - [수학의 재미/행렬 이론] - 행렬이 양수다? positive semidefinite 에 positive definite의 정의와 이 행렬이 만족하는 성질을 다뤘습니다. 바로
○ 고윳값 $\lambda_i$ 들은 음이 아닌 실수
라는 것이죠.
이제 다 됐습니다.
2022.07.04 - [수학의 재미/행렬 이론] - 공분산과 공분산 행렬 글을 보면,
공분산 행렬은 positive definite 행렬이다.
라는 얘기를 했습니다. 또한, 수식(2)의 공분산 행렬 $\mathbf{C}$ 은 positive definite 행렬이므로 모든 것을 정리하면 이렇습니다.
주성분 분석 결론
주성분 분석
○ 고윳값 $\lambda_i$ 들은 음이 아닌 실수이다. 즉, $\mathbf{D}$는 원소가 모두 음이 아닌 대각행렬이다.
$p$개의 고윳값을 순서대로 배열하여
$$\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_p$$
라 합시다. 각각의 고윳값에 대응하는 고유벡터를 $\mathbf{w}_i$라 하면,
○ 고유벡터 $\mathbf{w_i}$들은 서로 직교(orthogonal) 한다. 즉
$$ \mathbf{W}= \begin{pmatrix} \mid & \mid & & \mid \\ \mathbf{w_1} & \mathbf{w_2} & \cdots &\mathbf{w_p} \\ \mid & \mid & & \mid \end{pmatrix} $$
는 직교행렬(orthogional matrix)이다. 또한,
$$ \mathbf{D}= \begin{pmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & &\ddots & \\ & & & \lambda_p \end{pmatrix} $$
라 하면
○ 다음의 행렬분해가 성립한다.
$$ \mathbf{C} = \mathbf{WDW^t}\tag{3}$$
주성분 분석의 의의
주성분 분석에서 등장하는 고윳값 $\lambda_i$ 들과 그에 해당하는 고유벡터 $\mathbf{w_i}$들은 어떤 의의가 있을까요?
고유벡터 $\mathbf{w_i}$들은 $\mathbb{R}^p$의 새로운 직교 좌표계이다.
고유값 분해를 통해 얻은 행렬 $\mathbf{W}$ 가 직교행렬이므로 각각의 열벡터 $\mathbf{w_i}$들은 직교합니다. 또한, 벡터 크기가 모두 1이죠. 따라서 표준 직교 좌표계와는 다른, 데이터들을 설명할 수 있는 또 다른 좋은 축이 됩니다.
아래 그림은 주성분 분석(Principal Component Analysis)이란?이라는 글에서 소개한 타원 형태의 자료인데
표준 직교 좌표계인 $\{(1,0) , (0,1)\}$ (검은색 축들)로 설명도 가능하고, 빨간색 축들로도 데이터를 설명할 수 있죠.
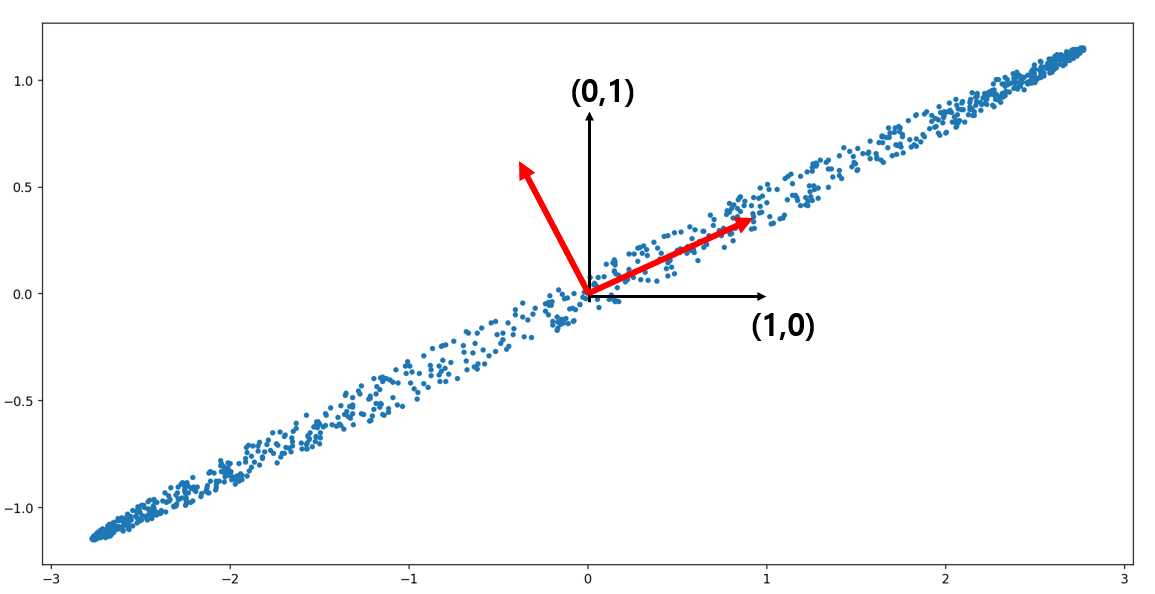
데이터 $\{\mathbf{x}_n , n=1,2,\cdots,N\}$ 을 축 $\mathbf{w_i}$에 정사영시켰을 때 좌표는 $ \{\mathbf{x}_n\cdot w_i \}$이다.
일반적으로 벡터 $\mathbf{x}$를 벡터 $\mathbf{y}$에 정사영시킨 벡터는
$ (\mathbf{x\cdot y}) \mathbf{y}$ 입니다. 따라서 문제의 벡터 $\mathbf{x_n}$을 $\mathbf{w_i}$에 정사영 시킨 벡터는
$$ (\mathbf{x_n\cdot w_i}) \mathbf{w_i}$$
입니다. 그런데 $\| \mathbf{w}_i\|=1$ 이죠. 따라서 좌표는
$$\mathbf{x_n\cdot w_i}$$
가 됩니다.
고윳값 $\lambda_i$들은 축 $\mathbf{w_i}$로 정사영시킨 데이터들의 분산이다.
데이터를 $\mathbf{w_i}$로 정사영 시키면 좌표들이
$$\{ \mathbf{x_n}\cdot \mathbf{w}_i ~,~ n=1,2,\cdots, N\}$$
이 된다고 하였습니다. 따라서 분산을 구해보면
$$
\begin{align}
\mathbb{V}(\mathbf{x}_n\cdot \mathbf{w}_i) &= \mathbb{E}((\mathbf{x}_n\cdot \mathbf{w}_i)^2 )-\mathbb{E}(\mathbf{x}_n\cdot \mathbf{w}_i)^2 \\
&= \frac1N (\mathbf{Xw}_i)^t (\mathbf{Xw}_i) -( \mathbb{E}(\mathbf{x_n}) \cdot \mathbf{w_i})^2 \\
& = \frac1N \mathbf{w}_i^t \mathbf{X}^t \mathbf{X} \mathbf{w}^t - 0\\
& = \mathbf{w_i}^t \mathbf{C} \mathbf{w_i} \\
& = \mathbf{w_i}^t \lambda_i \mathbf{w_i} \\
& = \lambda_i \|\mathbf{w}_i\|^2 \\
& = \lambda_i
\end{align}
$$
애당초, 데이터 $\mathbf{x_i}$ 들의 평균이 $\mathbf{0}$이므로 세 번째 등식이 성립하고, 마지막 등식에서는 $\lambda_i$가 $\mathbf{w_i}$에 대응하는 고유값이라 $\mathbf{C w_i} = \lambda_i \mathbf{w_i}$ 가 성립하기 때문입니다.
차원의 축소
드디어 주성분 분석의 주목적인 차원의 축소(reduction of dimension)에 도달했습니다. 위에서 구한 $\lambda_i$ 들은 지금 $$\lambda_1 \geq \lambda_2 \geq \cdots \lambda_p$$
로 크기 순서대로 줄 서 있습니다. 그런데 뒤에 있는 고윳값들이 거의 0이어서 무시할만하다고 합시다.

고윳값들은 분산의 개념이었습니다. 따라서 무시할만한 고윳값들에 대해선 해당 고유 벡터 쪽으로 데이터가 똘똘 뭉쳐서(즉, 분산이 작아서) 차원이 축소가 된다는 이야기죠. 수학적으로 써볼까요?
식(3)에 등장한 대각행렬 $\mathbf{D}$에서 처음 $q$개만 살아있고, 나머지 $p-q$개 고윳값은 모두 0 근처라 해봅시다.
$$
\mathbf{D}=
\begin{pmatrix}
\lambda_1 & & & & & \\
& \ddots & & & & & \\
& & \lambda_q & & & \\
& & & 0 & & \\
& & & & \ddots & \\
& & & & & 0 \\
\end{pmatrix}
$$
그러면 0이 있는 부분을 제외하고
$$
\mathbf{D_q}=
\begin{pmatrix}
\lambda_1 & & \\
& \ddots & & \\
& & \lambda_q
\end{pmatrix}
$$
라 쓴다면 데이터 벡터 $\mathbf{X}$는
$$ \mathbf{X}\mathbf{W_q} \approx \mathbf{W_q} \mathbf{D_q}$$
라 쓸 수 있습니다. 여기서 $\mathbf{W}_q$는
$$ \mathbf{W_q}= \begin{pmatrix} \mid & \mid & & \mid \\ \mathbf{w_1} & \mathbf{w_2} & \cdots &\mathbf{w_q} \\ \mid & \mid & & \mid \end{pmatrix} $$
즉, 처음 고유벡터 $q$개를 열 벡터로 하는 행렬이죠.
따라서 $q$개의 축으로, 의미 있는 $q$개의 분산을 가질 수 있도록 데이터를 설명 가능한 것입니다.
마치 아래 그림을 그냥 직선으로 보고 싶은 욕망처럼요.
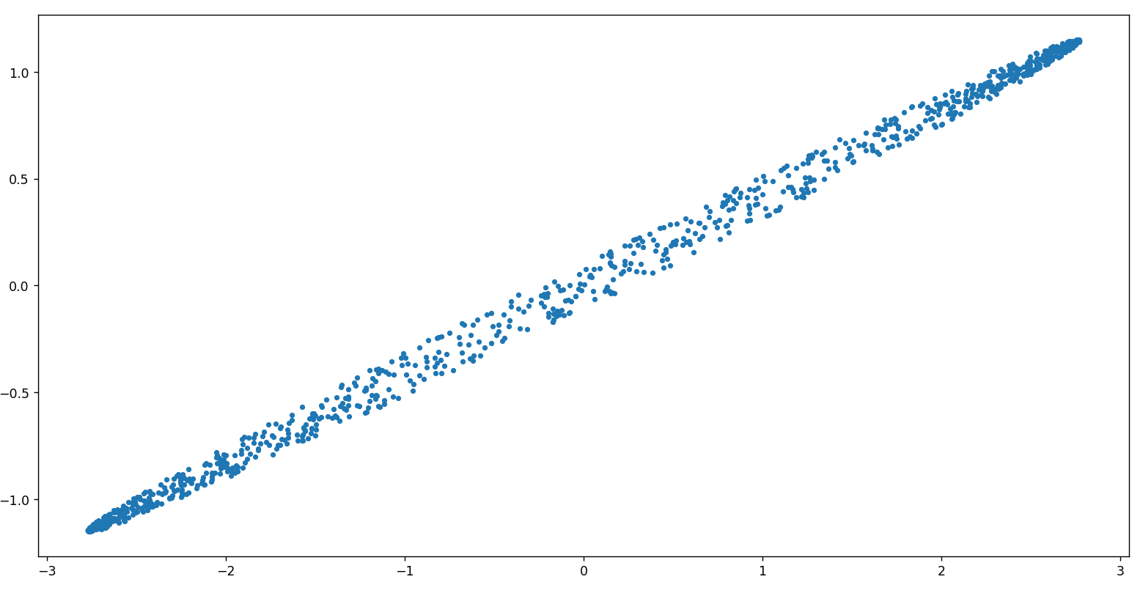
다음 글에서는 실제 예제를 통하여 주성분 분석을 해보도록 하겠습니다.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| FDM #8, Wave Equation(파동방정식)의 풀이(1) (0) | 2023.01.27 |
|---|---|
| 주성분 분석(PCA) 예제 - 타원 내부 데이터 (0) | 2022.09.11 |
| 주성분 분석(PCA)의 수학적 접근 (0) | 2022.09.05 |
| 주성분 분석(Principal Component Analysis)이란? (2) | 2022.09.02 |
| FDM #7, Heat Equation의 풀이(3) (0) | 2022.08.01 |




댓글