이 글은
FDM #7, Heat Equation의 풀이(3)
이 글은 2022.08.01 - [수학의 재미/아름다운 이론] - FDM #6, Heat Equation의 풀이(2) FDM #6, Heat Equation의 풀이(2) 이 글은 2022.07.30 - [수학의 재미/아름다운 이론] - FDM #5, Heat Equation의 풀이(1) FDM #5, Heat Equation
sine-qua-none.tistory.com
에 이어서 유명한 편미분방정식을 FDM으로 해결하는 방법을 알아보겠습니다.
바로, Wave Equation이라 불리는 편미분 방정식을 FDM으로 풀어볼 생각입니다.
Wave Equation은 파동방정식이라 불리는 것으로서, $\sin$함수와 $\cos$함수와 긴밀한 관련이 있습니다. 두 함수가 파동을 나타내는 함수이기에 Wave라는 단어가 어색하지 않습니다.
Wave Equation의 대표적인 형태
Wave Equation의 대표적이고 간단한 형태는 아래와 같습니다. 함수 $u(t,x)~, t\geq 0, 0\leq x\leq L$이
$$ \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}, ~~ 0<x<L\tag{W.E.}$$
$$ u(t,0) =0~~, u(t,L)=0 \tag{B.C}$$
$$ u(0,x)=f(x) \tag{I.C} $$
$$ \frac{\partial u}{\partial t}(0,x) = g(x)$$
의 관계식을 만족할 때, 이 관계식을 Wave Equation이라 부릅니다. B.C는 경계 조건(boundary condition), I.C.는 초기조건(initial condition)을 뜻합니다.
그림으로 표시하면 아래와 같죠. 아래 그림처럼, 경계조건과 초기조건으로 둘러싸인 영역에, 초기 속도가 주어진다면, 주어진 영역에서 Wave equation을 풀 수 있게 됩니다.

편미방을 격자판으로 이산화
위 그림을 이산화(discretization)시켜보겠습니다.
적절한 만기시점 $T$를 하나 잡고, $[0, T]$구간을 아래처럼 $N$ 등분합니다.
$$ 0=t_0<t_1<\cdots<t_{N-1}<t_N=T$$
또 $x$의 최솟값을 $x_m$, 최댓값을 $x_M$이라 하고, 구간 $[x_m, x_M]$을 $J$등분합니다(위 그림에서는 $x_m =0$.)
$$ x_m = x_0 <x_1<\cdots <x_J =x_M$$
$t,x$ 등분 간격을 각각 $k,h$라 합시다. 즉,
$$ k=t_1-t_0~,~ h=x_1-x_0$$ 입니다.
또 기호 $u_j^n$을
$$ u_j^n := u(t_n ,x_j)~,~0\leq n\leq N~,~ 0\leq j\leq J$$
라 정의합니다. 이제 진짜 이산화에 돌입해 보죠.
점 $(t_n,x_j)$에서
$$ \frac{\partial^2 u}{\partial t^2} \approx \frac{u_j^{n+1} -2u_j^n + u_j^{n-1}}{k^2}$$
이고
$$ \frac{\partial^2 u}{\partial x^2} \approx \frac{u_{j+1}^{n} -2u_j^n + u_{j-1}^{n}}{h^2}$$
입니다. 따라서 식 (W.E)는
$$ \frac{u_j^{n+1} -2u_j^n + u_j^{n-1}}{k^2}=c^2 \frac{u_{j+1}^{n} -2u_j^n + u_{j-1}^{n}}{h^2}$$
입니다. 만일
$$ r = \frac{ck}{h}$$ 라 하면 위 식은
$$ \underbrace{u_j^{n+1}}_{t:=n+1} =\underbrace{ r^2 u_{j+1}^n + 2(1-r^2) u_j^n + r^2 u_{j-1}^n}_{t:=n} -\underbrace{ u_j^{n-1}}_{t=n-1} \tag{1}$$
로 표현됩니다. 잘 보면 식 (1)는 즉 시점 레벨 $n+1$으 값이 $n$과 $n-1$에서의 값들로 표현된다는 뜻이죠.
이제 위 그림을 격자로 아래와 같이 표현합니다.

그랬을 때, 시점 $n-1, n, n+1$ 과 $x$의 레벨 $j-1,j,j+1$사이에는 아래와 같은 관계성이 있습니다.

$n+1$ 시점의 $j$번째 $x$는 $n$번째 시점의 세 값과 $n-1$번째의 한 값이 영향을 줍니다.
또한 Boundary condition은 식 (BC)이므로
$$ u_0^n= u_J^n =0,~~ \forall n\leq N \tag{2}$$
입니다.
initial condition은 식(IC)에서
$$ u_j^0 = f(j) ~,~ \forall j\leq J \tag{3}$$입니다. 따라서 $u$의 격자판 중 아래 그림 속의 녹색값들이 주어진 값들이 됩니다.
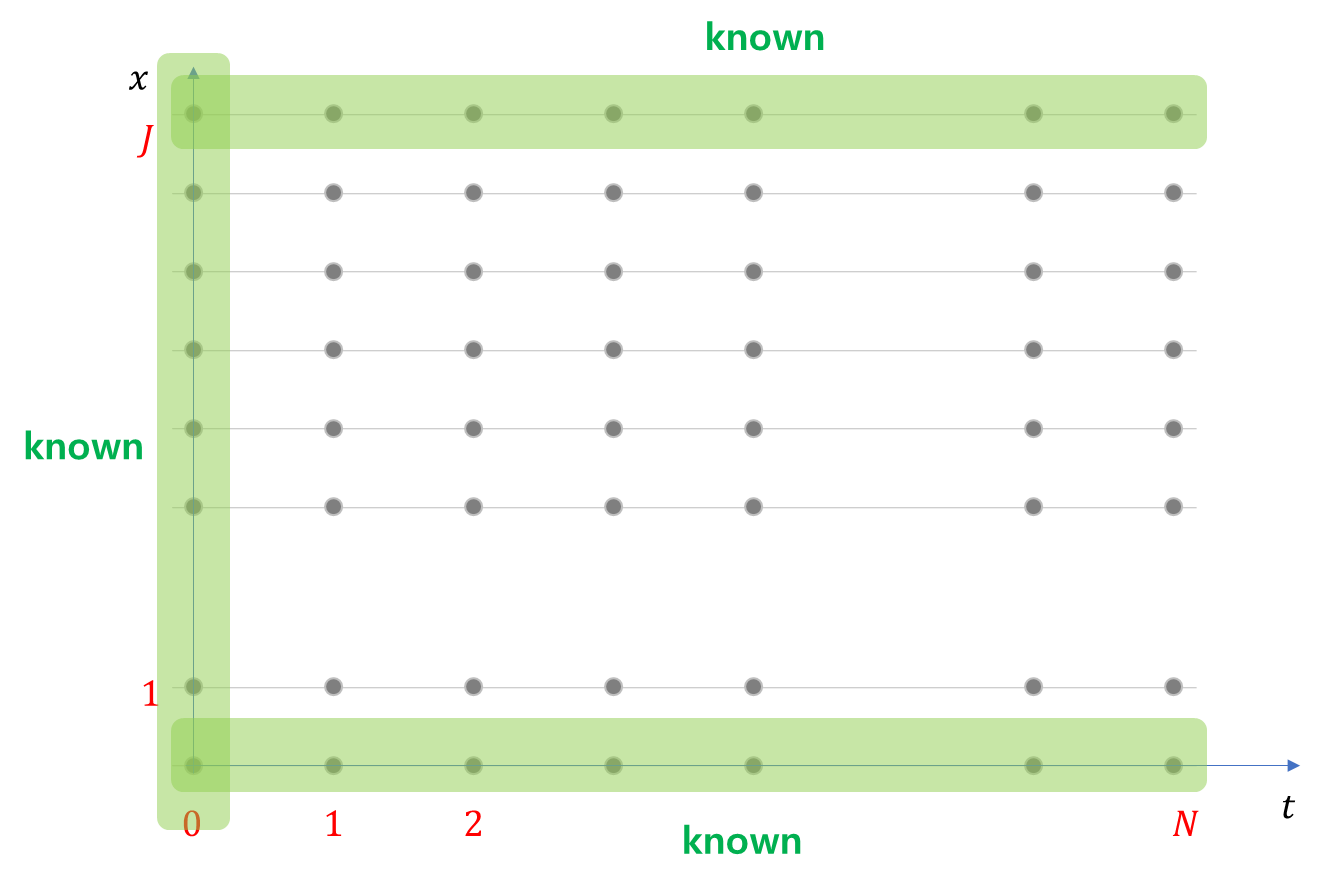
이제 시점 축 $t$ 축으로 움직이면서 격자판의 값들을 결정해야 하는데요. 처음부터 난관에 봉착합니다. 아래 녹색테두리 영역은 어떻게 구할까요?
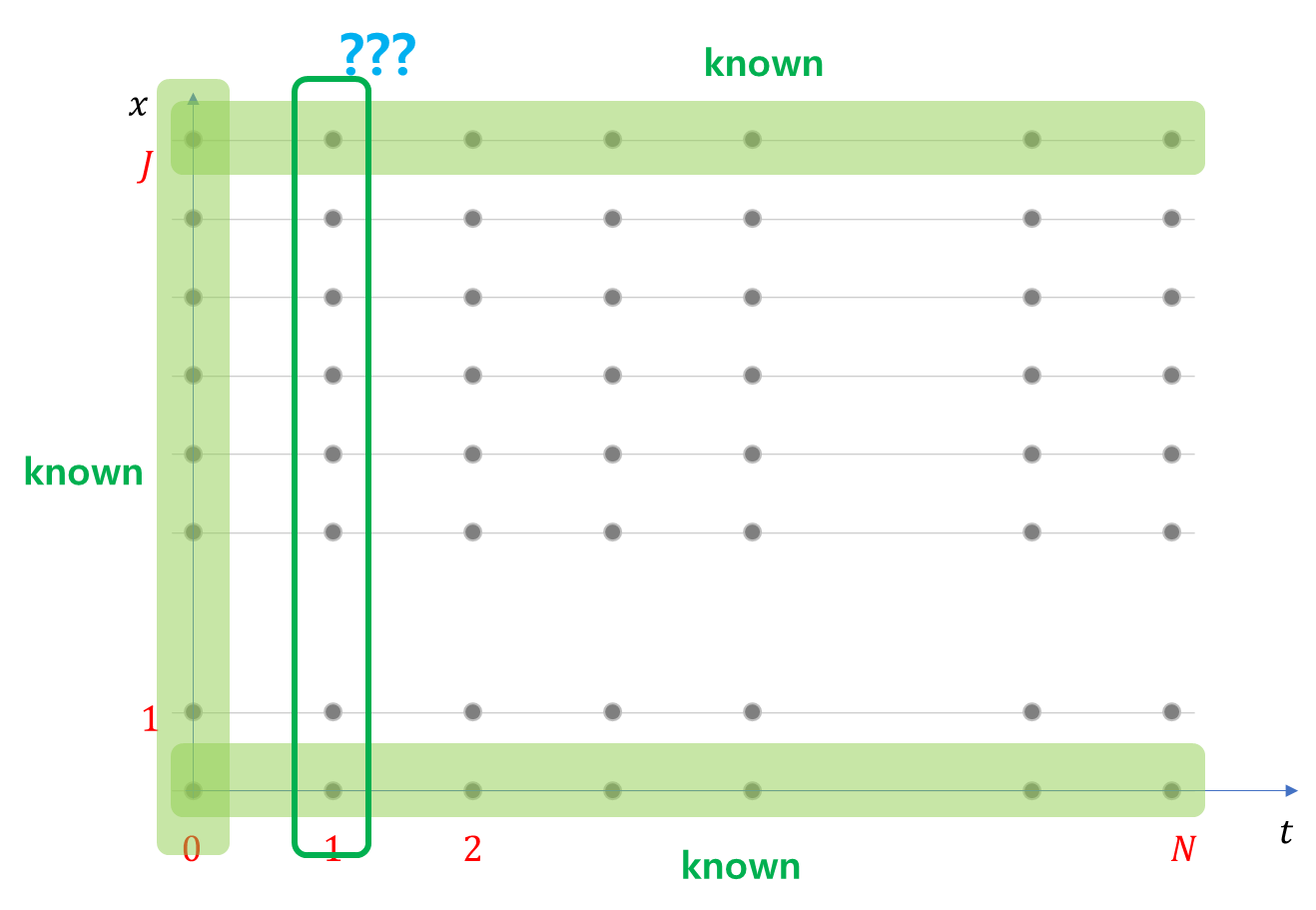
식 (1)에 따르면 위 녹색테두리 영역 $(t=1)$ 을 계산하기 위해서는 $t$ 인덱스가 두 개가 필요합니다. 전 시점과 전전 시점이죠. 즉 $t=0$과 $t=-1$입니다.
이를 해결하기 위해 다음의 세 방법이 있습니다. Wave Equation의 마지막 조건이었던
$$ \frac{\partial u}{\partial t}(0,x) = g(x)$$
를
1. Forward Difference (전방 차분)으로 구하기
2. Central Difference (중앙 차분)으로 구하기
3. Backward Difference(후방 차분)으로 구하기
간단하게 살펴보겠습니다.
| 1. Forward Difference |
| 전방차분으로는 $$ \frac{\partial u}{\partial t}(0,x) = \frac{ u_j^1-u_j^0}{k} = g(x_j)$$ 이므로 모든 $j$에 대해 $$ u_j^1 = kg(x_j)+u_j^0$$ 입니다. 따라서 시점 레벨 $1$일 때가 완비되었으므로, 시점 레벨 2부터 쭉 식(1)에 따라 구할 수 있죠. |
| 2. Central Difference |
중앙차분으로는 $$ \frac{\partial u}{\partial t}(0,x) = \frac{ u_j^1-u_j^{-1}}{2k} = g(x_j)$$ 이므로 모든 $j$에 대해 $$ u_j^{-1} = u_j^1 - 2kg(x_j)$$ 입니다. 따라서 식 (1)에 $n=0$을 대입하여 $$ \begin{align} u_j^1 &= r^2 u_{j+1}^0 + 2(1-r^2) u_j^0 + r^2 u_{j-1}^0 - u_j^{-1}\\ &= r^2 u_{j+1}^0 + 2(1-r^2) u_j^0 + r^2 u_{j-1}^0 - u_j^1 + 2kg(x_j) \end{align} $$ 따라서 $$ u_j^1 =\frac12 \left( r^2 u_{j+1}^0 + 2(1-r^2) u_j^0 + r^2 u_{j-1}^0\right) +kg(x_j)$$ 로 구할 수 있습니다. 이제 시점 레벨 1일 때를 구하였으므로 2 이상의 시점 레벨을 모두 채울 수 있습니다. |
| 3. Backward Difference |
| 후방차분으로는 $$ \frac{\partial u}{\partial t}(0,x) = \frac{ u_j^0-u_j^{-1}}{k} = g(x_j)$$ 이므로 모든 $j$에 대해 $$ u_j^{-1} = u_j^0 - kg(x_j)$$ 입니다. 따라서 식 (1)에 $n=0$을 대입하여 $$ \begin{align} u_j^1 &= r^2 u_{j+1}^0 + 2(1-r^2) u_j^0 + r^2 u_{j-1}^0 - u_j^{-1}\\ &= r^2 u_{j+1}^0 + 2(1-r^2) u_j^0 + r^2 u_{j-1}^0 - u_j^0 + kg(x_j) \end{align} $$ 따라서 $$ u_j^1 =\left( r^2 u_{j+1}^0 + (1-2r^2) u_j^0 + r^2 u_{j-1}^0\right) +kg(x_j)$$ 로 구할 수 있습니다. 이제 시점 레벨 1일 때를 구하였으므로 2 이상의 시점 레벨을 모두 채울 수 있습니다. |
이제 시점 레벨 1을 구할 수 있습니다. 그러면
○ 시점 레벨 2의 모든 값 $u_j^2$는 $u_j^1$들과 $u_j^0$들을 조합하여 식(1)으로 구한다.
○ 시점 레벨 3의 모든 값 $u_j^3$는 $u_j^2$들과 $u_j^1$들을 조합하여 식(1)로 구한다...
이런 식으로 모든 $n\leq N$에 대해 구할 수 있게 됩니다.
예제 : Python Code
다음의 Wave Equation을 FDM으로 풀고, 원래 해와 맞는지를 한번 확인해 보겠습니다.
Wave Equation의 예시
$$ \begin{align} \frac{\partial^2 u}{\partial t^2} &= c^2 \frac{\partial^2 u}{\partial x^2}, ~~ 0<x<1\\ u(t,0)& =0, \\ u(t,1)&=0\\ u(0,x)&=\sin(5\pi x) + 2\sin(7 \pi x)\\ \frac{\partial u}{\partial t}(0,x) &= 0 \end{align} $$
정확한 해는
$$ u(x,y) = \sin(5 \pi x) \cos(5c \pi t) + 2\sin(7 \pi x) \cos(7c \pi t)$$
위 식 (B.C)의 $f(x) = sin(5\pi x) + 2\sin(7 \pi x)$이고 속도의 초기조건 $g(x)=0$인 상황이네요.
아래는 Python Code입니다.
import numpy as np
import matplotlib.pyplot as plt
def Solve_WaveEquation():
# -----------------------------------------------------------------
# u_{tt} = c^2 u_{xx} for all 0<x<1 and t>0
# u(t,0) =u(t,1) =0 for all t>0
# u(0,x) = sin(5πx) + 2sin(7πx) for all 0<x<1
# u_t(0,x)=0
#
# solution : u(x,y) = sin(5πx)cos(5cπt) + 2sin(7πx)cos(7cπt)
# -----------------------------------------------------------------
#
# set parameters
t_min = 0
t_max = 1
x_min = 0
x_max = 1
const = 2 # 예제의 c 값에 해당, 2로 둔다.
## Nize = time_size, Jsize = xsize
Nsize, Jsize = 200, 100 # 시간은 [0,1] 시간 200등분, x는 [0,1] 구간 100등분
x_seq = np.linspace(x_min, x_max, Jsize + 1)
t_seq = np.linspace(t_min, t_max, Nsize + 1)
h = x_seq[1] - x_seq[0] # x level 등분간격
k = t_seq[1] - t_seq[0] # time level 등분가격
r = const * k / h # 위 설명에서의 r
print('r={}'.format(r)) # r값에 따라 이 문제가 풀릴수도, 안풀릴수도 있다. 출력하여 확인
# solution grid u setting
u = np.empty((Nsize + 1, Jsize + 1))
# initial_condition
PI = np.pi
u[0, :] = np.sin(5 * PI * x_seq) + 2 * np.sin(7 * PI * x_seq) #initial condition
u[:, 0] = 0 # boundary condition
u[:, -1] = 0 # boundary condition
#u_t(0,x)=g(x)의 세가지 세팅 (g(x)=0 인 상황)
# u_t(0,x) 조건 세가지(forward, central, backward 를 모두 구현)
# 하나씩 주석을 풀어 확인해볼수 있다.
# u_t(0,x) 조건의 forward difference
# u[1, :] = u[0, :]
# u_t(0,x) 조건의 central difference
u[1, 1:Jsize] = 0.5 * (r ** 2) * u[0, 2:Jsize + 1] + (1 - r ** 2) * u[0, 1:Jsize] + \
0.5 * (r ** 2) * u[0, 0:Jsize - 1]
# u_t(0,x) 조건의 backward difference
# u[1, 1:Jsize] = (r ** 2) * u[0, 2:Jsize + 1] + (1 - 2 * r ** 2) * u[0, 1:Jsize] + \
# (r ** 2) * u[0, 0:Jsize - 1]
# recursive formula
for n in range(1, Nsize):
u[n + 1, 1:Jsize] = (r ** 2) * u[n, 2:Jsize + 1] + \
2 * (1 - r ** 2) * u[n, 1:Jsize] + \
(r ** 2) * u[n, 0:Jsize - 1] - u[n - 1, 1:Jsize]
fdm_solution = u[-1, :] # 시점이 t_seq[-1]일 때 즉 t=t_max 일때의 u의 값
# 값비교를 위해 exact formula 를 구현
exact_solution = np.sin(5 * PI * x_seq) * np.cos(5 * const * PI * t_max) + \
2 * np.sin(7 * PI * x_seq) * np.cos(7 * const * PI * t_max)
plt.plot(x_seq, fdm_solution, label='fdm_solution')
plt.plot(x_seq, exact_solution, label='exact_solution')
plt.title('Exact vs FDM')
plt.legend()
plt.show()
print(fdm_solution-exact_solution) # 실제값과 fdm의 값 차이 비교를 위해 차이출력
if __name__ == '__main__':
Solve_WaveEquation()
함수 $g(x)=0$이어서 조건이 좀 많이 간단해진 코드입니다. 결과를 보시죠.
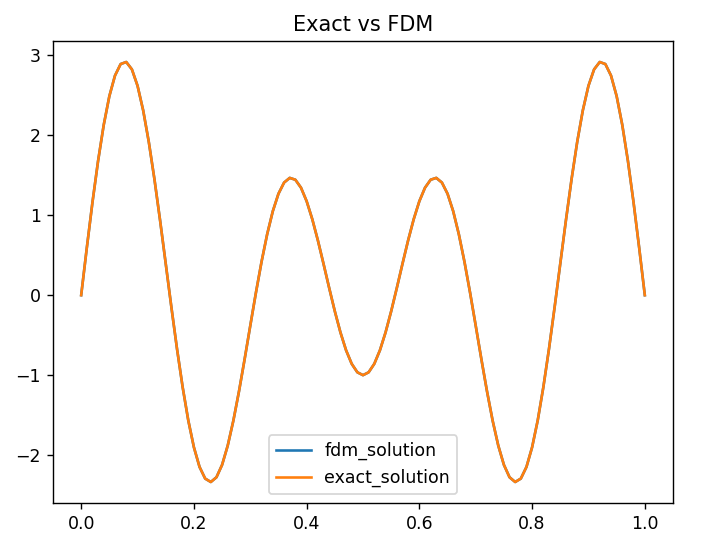
너무 정확한 구현으로 파란색 fdm 결과선이 아예 보이지 않습니다.
출력결과를 보면,
r=1.0
[ 0.00000000e+00 2.22044605e-16 1.99840144e-15 -4.44089210e-16
-8.88178420e-16 8.88178420e-16 -5.77315973e-15 1.33226763e-15
-2.66453526e-15 -4.44089210e-16 -1.77635684e-15 -2.22044605e-15
4.44089210e-16 -2.22044605e-16 1.33226763e-15 -2.10942375e-15
2.88657986e-15 -2.33146835e-15 8.88178420e-16 -2.66453526e-15
-4.44089210e-16 -3.99680289e-15 4.44089210e-16 -4.44089210e-15
-1.77635684e-15 -7.99360578e-15 -1.77635684e-15 -7.10542736e-15
3.33066907e-15 -7.66053887e-15 1.44328993e-15 -6.43929354e-15
2.88657986e-15 -6.21724894e-15 8.88178420e-16 -7.10542736e-15
4.44089210e-16 -6.88338275e-15 -4.44089210e-16 -5.10702591e-15
2.22044605e-16 -5.55111512e-15 3.33066907e-16 -4.88498131e-15
1.60982339e-15 -4.66293670e-15 0.00000000e+00 -6.77236045e-15
1.44328993e-15 -4.10782519e-15 4.44089210e-16 -5.21804822e-15
-4.44089210e-16 -4.88498131e-15 7.77156117e-16 -6.10622664e-15
3.88578059e-16 -6.05071548e-15 -5.55111512e-16 -5.88418203e-15
-1.33226763e-15 -5.99520433e-15 -1.33226763e-15 -5.10702591e-15
-1.77635684e-15 -5.32907052e-15 -1.77635684e-15 -3.21964677e-15
-1.11022302e-15 -4.88498131e-15 -7.77156117e-16 -3.33066907e-15
8.88178420e-16 -3.55271368e-15 2.22044605e-16 -5.32907052e-15
4.44089210e-16 -8.43769499e-15 -2.22044605e-15 -8.43769499e-15
-1.99840144e-15 -1.04360964e-14 -2.22044605e-16 -1.15463195e-14
0.00000000e+00 -1.00475184e-14 1.55431223e-15 -1.19904087e-14
3.33066907e-15 -7.99360578e-15 1.77635684e-15 -1.02140518e-14
5.32907052e-15 -5.32907052e-15 1.77635684e-15 -2.22044605e-15
0.00000000e+00 -4.44089210e-16 2.22044605e-16 0.00000000e+00
-2.32682892e-15]
$r$ 값은 1이고, FDM과 원래 해의 차이는 0이라 봐도 무방하겠습니다.
참고로 이 $r$은 Courant Number(쿠란트 넘버)라는 숫자입니다. 이 값에 따라서 FDM 방법이 유효할 수도, 유효하지 않을 수도 있습니다.
만일,
Nsize, Jsize = 200, 200와 같이, $x$ 구간을 200 분할해 보면, Courant Number $r$은 2가 됩니다.
이때의 결과는
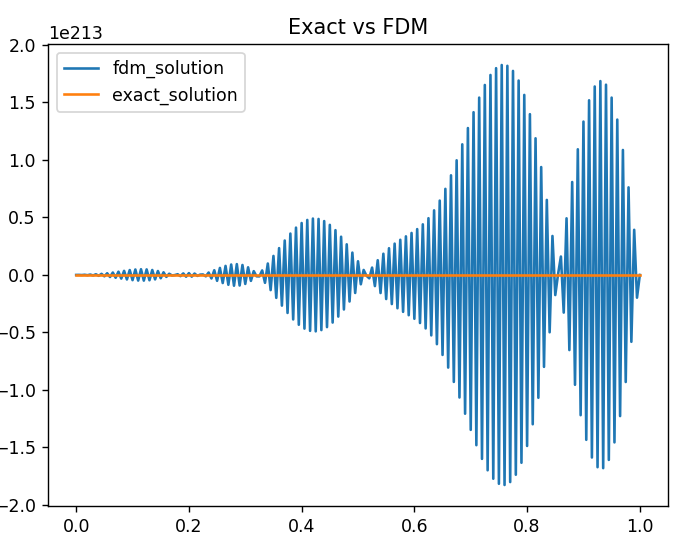
r=2.0
[ 0.00000000e+000 4.52343235e+209 -9.52132140e+209 1.54652233e+210
-2.28193885e+210 3.20335212e+210 -4.35317128e+210 5.76970251e+210
-7.48517740e+210 9.52341765e+210 -1.18972642e+211 1.46059537e+211
...
-2.32682892e-015]말도 안 되는 차이입니다.
Courant Number의 값에 따라 왜 이런 차이가 나는지 다음 글에서 간단히 설명해 보겠습니다.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| FDM #10, Laplace Equation의 풀이(2) Python Code (0) | 2023.02.02 |
|---|---|
| FDM #9, Laplace Equation의 풀이(1) (0) | 2023.02.02 |
| 주성분 분석(PCA) 예제 - 타원 내부 데이터 (0) | 2022.09.11 |
| 주성분 분석(PCA)의 수학적 접근 #2 (2) | 2022.09.06 |
| 주성분 분석(PCA)의 수학적 접근 (0) | 2022.09.05 |




댓글