이 글은
2022.08.01 - [수학의 재미/아름다운 이론] - FDM #6, Heat Equation의 풀이(2)
FDM #6, Heat Equation의 풀이(2)
이 글은 2022.07.30 - [수학의 재미/아름다운 이론] - FDM #5, Heat Equation의 풀이(1) FDM #5, Heat Equation의 풀이(1) 이번 글은 2022.07.25 - [수학의 재미/아름다운 이론] - 미분방정식을 연립방정식으로, F..
sine-qua-none.tistory.com
에서 이어집니다.
지난 글의 똑같은 문제를 다른 방식의 FDM으로 접근해 보겠습니다.
열방정식의 예시(Revisited)
저번 글에서 다루었던 예시는 다음과 같습니다.
$$u_t(t,x) = u_{xx}(t, x), 0<x<1, t>0, \tag{1}$$
○ 초기 조건: $ u(0,x) = \sin(\pi x) $
○ 경계조건: $ u(t,0)= u(t,1) =0 $
※ 참고 이 방정식의 exact solution 은
$$u(t,x)= \sin(\pi x)\exp (-\pi^2 t)\tag{2}$$
이산화 과정(지난 글과 똑같으므로 건너뛰어도 됨)
저번 글에서 알아보았듯이 시점 변수 $t$와 변위 변수 $x$를 다음과 같이 격자로 나눕니다.
열방정식의 이산화 과정
1. 시간 $t$ 축을 유한개의 균등 격자로 나눔
- 식(1)에는 초기시점 $t=0$은 있지만, 끝시점은 없죠. 따라서 관심 있는 충분히 큰 끝시점 $T$를 하나 정하고,
$$ 0= t_0 < t_1 <t_2 <\cdots < t_{N-1} < t_N =T$$
로 균등하게 나눔
- 각 시점의 차이는 $k$로 일정함. 즉, $t_{n+1}-t_n =k$
2. 변위 변수 $x$도 유한개의 균등 격자로 나눔
- 식(1)의 $x$가 움직이는 구간을 $[x_m, x_M]$이라 했을 때,
$$ x_m =x_0 < x_1 <x_2 < \cdots < x_{J-1} < x_J = x_M$$
으로 균등하게 나눔
- 각 변위의 차이는 $h$로 일정함. 즉, $x_{j+1}-x_j = h$
이제 $(t,x)$를 격자를 사용하여 편미분 방정식을 연립방정식으로 만들어 보겠습니다.
FDM 설계
이제 $(t,x)$를 격자를 사용하여 편미분 방정식을 연립방정식으로 만들어 보겠습니다.
$$0=t_0 <t_1 <\cdots <t_n =T$$와
$$x_m = x_0 < x_1 <\cdots < x_J =x_M$$
에 대해 식(1)을 아래의 방법으로 이산화 시킵니다. $t$ 수열 사이 간격은 $k$, $x$수열 사이 간격은 $h$입니다.
시점 $t_n$에서 backward difference 방식으로 이산화 시키자!
그러면 점 $(t_{n+1} ,x_j)$에서 $k$ 만큼의 시점 차로 backward difference를 구하면
$$ u_t(t_{n+1} , x_j) = \frac{u(t_{n+1}, x_j)-u(t_{n+1}-k, x_j)}{k }$$이고
$ t_{n+1}-k=t_{n}$입니다.
저번 글과 마찬가지로 $u_j^n = u(t_n, x_j)$ 라 정의하면
$$ u_t(t_{n+1} , x_j ) = \frac{u_j^{n+1}- u_j^n}{k}\tag{2}$$
이죠. $x$에 대해서는 central difference를 사용합니다. $x$의 차이를 $h$라 하면
$$ u_{xx}(t_{n+1},x_j) = \frac{u(t_{n+1}, x_j+h)-2u(t_{n+1}, x_j)+u(t_{n+1}, x_j-h)}{h^2}$$
입니다. $x_j \pm h = x_{j\pm 1}$ 이므로 준식은
$$ u_{xx}(t_{n+1},x_j) = \frac{u_{j+1}^{n+1}-2u_j^{n+1} +u_{j-1}^{n+1}}{h^2}\tag{3}$$
따라서 $u_t(t,x) = u_{xx}(t,x)$는 식(2), (3)을 결합하여 다음과 같이 변합니다.
$$ \frac{u_j^{n+1}- u_j^n}{k} = \frac{u_{j+1}^{n+1}-2u_j^{n+1} +u_{j-1}^{n+1}}{h^2}$$
$\alpha= \frac{k}{h^2}$ 이라 하면
$$u_j^{n+1}- u_j^n = \alpha \left(u_{j+1}^{n+1}-2u_j^{n+1} +u_{j-1}^{n+1} \right) $$
정리하면
$$u_j^{n} = -\alpha u_{j-1}^{n+1}+(1+2\alpha) u_j^{n+1} -\alpha u_{j+1}^{n+1} \tag{*}$$
이걸 어떻게 해석해야 할까요?
$n+1$ step에 있는 $j-1 , j , j+1$ 번째 값 3개를 가지고 $n$ step의 $j$번째 값을 구할 수 있다???
위의 해석은 터무니없죠. 어떻게 미래 시점인 $n+1$의 정보를 가지고 과거 시점인 $n$을 구할 수 있나요. 따라서 다른 식으로 해석해 봅시다.

- $n$ step상의 $j$번째 점 하나가 $n+1$ step $j-1$, $j$, $j+1$ 번째 점에 영향을 미칩니다.(그림의 투명한 테트리스 블록 참조) 또한
- $n$ step상의 $j-1$번째 점 하나가 $n+1$ step $j-2, j-1$, $j$ 번째 점에 영향을 미칩니다.
- $n$ step상의 $j+1$번째 점 하나가 $n+1$step $j$, $j+1, j+2$ 번째 점에 영향을 미칩니다.
역으로 생각하면,
$n+1$ step의 $j$번째 값에 영향을 미치는 것은 $n$ step의 $j-1, j, j+1$번째 점
입니다. 좀 더 자세히 써봅시다.
식(*)은
| $j=1$일 때 | $$ u_1^n = -\alpha u_0^{n+1} +(1+2\alpha) u_1^{n+1} - \alpha u_2^{n+1} = (1+2\alpha) u_1^{n+1} -\alpha u_2^{n+1}$$ |
| $1<j<J-1$ 일 때, | $$u_j^{n} = -\alpha u_{j-1}^{n+1}+(1+2\alpha) u_j^{n+1} -\alpha u_{j+1}^{n+1}$$ |
| $j=J-1$일 때, | $$ u_{J-1}^n = -\alpha u_{J-2}^{n+1} +(1+2\alpha) u_{J-1}^{n+1} - \alpha u_{J}^{n+1} = -\alpha u_{J-2}^{n+1} +(1+2\alpha) u_{J-1}^{n+1}$$ |
라 쓸 수 있고, 마지막 단계로 위의 관계식을 행렬로 표현해보겠습니다.
$$
\begin{pmatrix}
1+2\alpha & -\alpha& & & \\
-\alpha & 1+2\alpha & -\alpha & & \\
& -\alpha & 1+2\alpha & \ddots & \\
& & \ddots & \ddots & -\alpha \\
& & & -\alpha & 1+2\alpha
\end{pmatrix}
\begin{pmatrix}
u_1^{n+1} \\
u_2^{n+1} \\
\vdots \\
u_{J-2}^{n+1} \\
u_{J-1}^{n+1}
\end{pmatrix}
=
\begin{pmatrix}
u_1^{n} \\
u_2^{n} \\
\vdots \\
u_{J-2}^{n} \\
u_{J-1}^{n}
\end{pmatrix}
$$
이 행렬 방정식의 행렬들을 차례대로 $T, \tilde{u}^{n+1}, \tilde{u}^n$ 이라 하면
$$ T \tilde{u}^{n+1} = \tilde{u}^n \tag{4}$$
입니다.
이제 FDM 푸는 절차를 얘기해보죠.
FDM 절차
아래와 같은 과정으로 모든 격자점에서의 $u$의 값을 산출합니다.
1. $u_j^0$ 산출, 즉 $t=0$에서의 값 산출
초기 조건을 이용하여 $u_j^0 = \sin(\pi x_j)$ 로 구함
2. $u_j^1$ 값 산출
$u_j^0$에서 양 끝점을 뺀 것이 $\tilde{u}^0$이고, 식(4)에서
$$ \tilde{u}^{1} = T^{-1} \tilde{u}^0 $$
으로 구하거나 아니면 $T$ 가 tridiagonal matrix 이므로 3중 대각행렬의 풀이법인 Thomas Algorithm을 사용하여 $\tilde{u}^1$ 산출. 여기에 경계조건 $u_0^1 = u_J^1 = 0$을 반영하여 온전한 형태의 $u_j^1$을 모두 얻음
3. $u_j^n$ 에서 $u_j^{n+1}$ 값 모두 산출
$u_j^n$을 다 알고 있으므로 여기서 양 끝점을 뺀 $\tilde{u}^n$ 을 구하고 2번과 같이 $T$의 역행렬이나 Thomas Algorithm을 사용하여 $\tilde{u}_j^{n+1}$ 을 얻음. 여기에 경계조건 $u_0^{n+1} = u_J^{n+1}=0$을 첨가하여 $u_j^{n+1}$을 모두 얻음
4. $u_j^N$ 까지 3번을 반복하여 모두 얻음
FDM 과정을 알아봤으니 직접 코딩하여 문제를 해결해 보겠습니다.
FDM 코드
python으로 작성한 위 문제의 FDM 풀이법은 다음과 같습니다.
def Solve_HeatEqaution_1D_implicit():
# u_t(t,x) = u_xx(t,x) 0<x<1, t>0
# u(0,x) = sin(πx)
# u(t,0)= u(t,1) =0
# closed form solution : u(t,x)= sin(πx)exp(-π^2 t)
x_min, x_max = 0, 1
t0 = 0
maturity = 1
num_x, num_t = 50, 10000
# num_x, num_t = 50, 4500
# num_x, num_t = 70, 10000
# num_x, num_t = 80, 10000
x_seq = np.linspace(x_min, x_max, num_x + 1)
t_seq = np.linspace(t0, maturity, num_t + 1)
h = x_seq[1] - x_seq[0]
k = t_seq[1] - t_seq[0]
alpha = k / h ** 2
print('delta of x : {:.3f}'.format(k))
print('delta of t : {:.3f}'.format(h))
print('alpha (= k/(h^2)) : {:.3f}'.format(alpha))
u = np.empty((num_t + 1, num_x + 1))
# u(t,x_min) =0
u[:, 0] = 0
# u(t, x_max) =0
u[:, -1] = 0
# u(0, x) = sin( pi*x)
u[0, :] = np.sin(np.pi * x_seq)
# construct coeff matrix : num_x -1 Size
diag = np.ones(num_x - 1) * (1 + 2 * alpha)
under = np.ones(num_x - 1) * (-alpha)
over = np.ones(num_x - 1) * (-alpha)
for n in range(num_t):
known = u[n, 1:num_x]
unknown = thomas(under, diag, over, known)
u[n + 1, 1:num_x] = unknown
t_idx = -1
real_t = t_seq[t_idx]
sol = np.sin(np.pi * x_seq) * np.exp(-np.pi * np.pi * real_t)
fdm_sol = u[t_idx, :]
max_of_difference = np.max(sol - fdm_sol)
print('max distance between exact solution and fdm solution is {:.4f}'.format(max_of_difference))
fig, axes = plt.subplots(1, 2, figsize=(10, 20))
axes[0].plot(x_seq, sol, 'b', label='exact solution')
axes[0].plot(x_seq, fdm_sol, 'm', label='fdm solution')
axes[0].set_title(' u(x) when k={:.3f}, h={:.3f}, alpha={:.3f}'.format(k, h, alpha))
axes[0].set_xlabel('x')
axes[0].set_ylabel('u(x)')
axes[0].legend()
axes[1].plot(x_seq, sol - fdm_sol, 'r')
axes[1].set_xlabel('x')
axes[1].set_ylabel('u(x)')
axes[1].set_title('difference between exact and fdm')
plt.show()
# Function for TMDA Algorithm
def thomas(a, b, c, d):
""" A is the tridiagnonal coefficient matrix and d is the RHS matrix"""
"""
a is lower diagonal a2,a3,..,a_N, meaning
b is diagonal b1,b2,b3,..,b_N meaning
c is upper diagonal c1,c2,c3,.. c_{N-1} meaning
"""
N = len(a)
cp = np.zeros(N, dtype='float64') # store tranformed c or c'
dp = np.zeros(N, dtype='float64') # store transformed d or d'
X = np.zeros(N, dtype='float64') # store unknown coefficients
# Perform Forward Sweep
# Equation 1 indexed as 0 in python
cp[0] = c[0] / b[0]
dp[0] = d[0] / b[0]
# Equation 2, ..., N (indexed 1 - N-1 in Python)
for i in np.arange(1, (N), 1):
dnum = b[i] - a[i] * cp[i - 1]
cp[i] = c[i] / dnum
dp[i] = (d[i] - a[i] * dp[i - 1]) / dnum
# Perform Back Substitution
X[(N - 1)] = dp[N - 1] # Obtain last xn
for i in np.arange((N - 2), -1, -1): # use x[i+1] to obtain x[i]
X[i] = (dp[i]) - (cp[i]) * (X[i + 1])
return (X)
if __name__ == '__main__':
Solve_HeatEqaution_1D_implicit()
간략히 살펴볼까요. 저번 글과 비슷한 부분들은 모두 생략합니다. (보다 자세한 설명은 여기를 참조). Thomas algorithm 부분도 생략합니다.
# construct coeff matrix : num_x -1 Size
diag = np.ones(num_x - 1) * (1 + 2 * alpha) # tridiagonal 의 주대각선을 설계
under = np.ones(num_x - 1) * (-alpha) # tridiagoal의 주대각선 아래대각선
over = np.ones(num_x - 1) * (-alpha) # tridiagoal의 주대각선 위대각선
for n in range(num_t):
known = u[n, 1:num_x] #u의 양 끝점을 뺀 뒤
unknown = thomas(under, diag, over, known) #thomas algorithm 적용
결과
다양한 격자에 대해 계산한 결과는 아래와 같습니다. exact solution과 FDM 결과의 차이 그래프도 수록합니다.
1. num_x, num_t = 50, 10000

2. num_x, num_t = 50, 4500
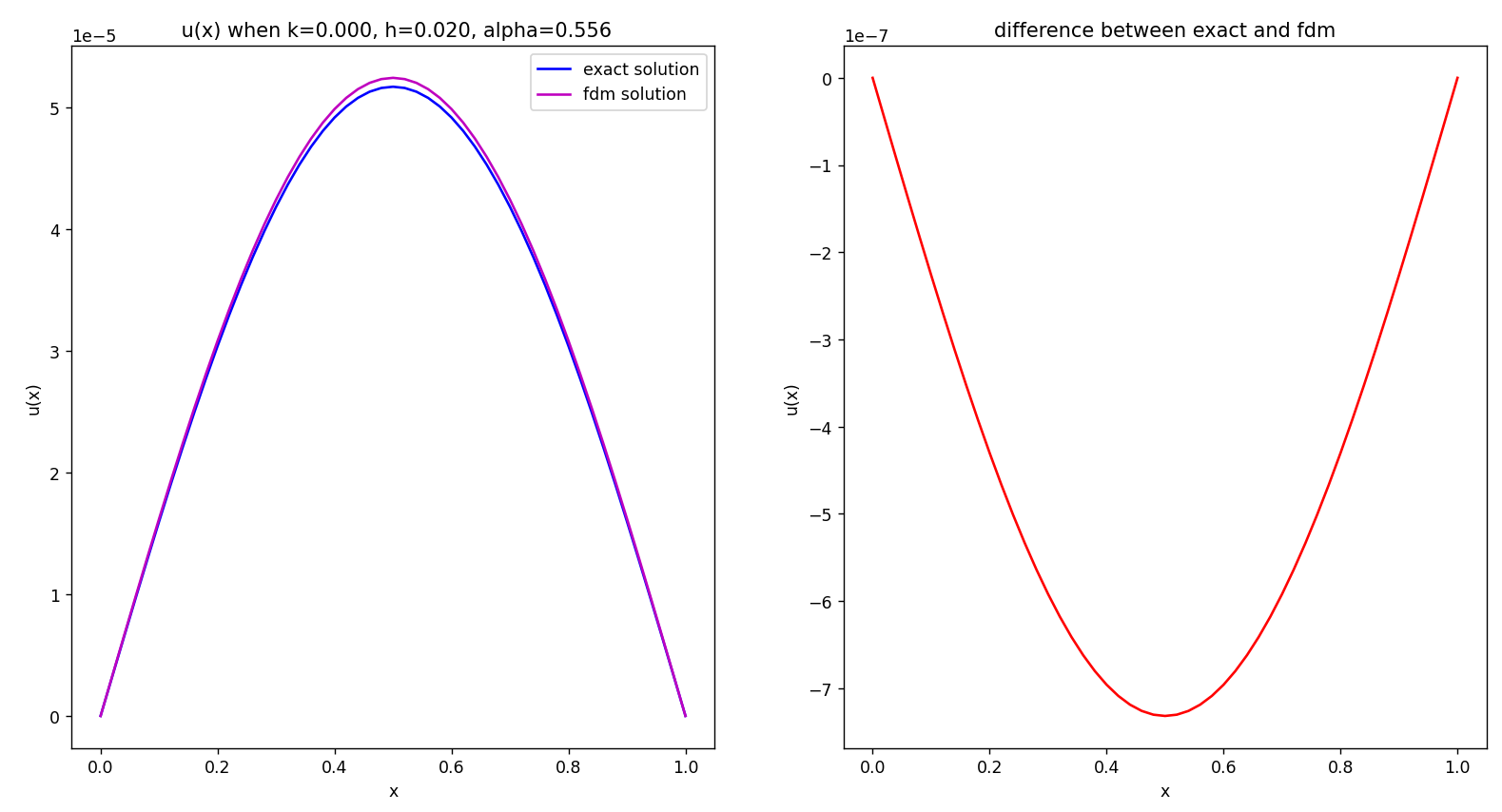
3. num_x, num_t = 70, 10000

4. num_x, num_t = 80, 10000

결론
FDM을 시점에 대해 backward difference로 놓았더니 다양한 격자에 대해 모두 좋은 결과가 나오는군요.
$\alpha$가 0.5보다 작은 것 여부에 상관없이 모든 경우에 대해 결과가 수렴합니다. 이렇게 bakward difference를 사용하여 FDM를 구성하고 푸는 방법을
함축적 방법(Implicit method)
이라고 합니다.
안정성 측면에서 implicit method를 사용하는 것이 좋으나, 위에서 보다시피 계산량이 많습니다. 행렬 방정식을 풀어야 하기 때문이지. 뿐만 아니고 3중대각행렬을 푸는 Thomas Algorithm도 곁들여 알아놓아야 합니다.
이상으로 Heat equation를 FDM으로 푸는 두 가지 방법인 explicit method와 implicit method를 모두 알아봤습니다. 이 heat equation 은 금융공학에서도 만나게 되는데, 파생상품의 가치가 만족하는 방정식이 바로 heat equation으로 나타나기 때문이죠.
이른바 Black Scholes Equation에 대해 다룰 때, 다시 이 글을 소환해 보도록 하겠습니다.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| 주성분 분석(PCA)의 수학적 접근 (0) | 2022.09.05 |
|---|---|
| 주성분 분석(Principal Component Analysis)이란? (2) | 2022.09.02 |
| FDM #6, Heat Equation의 풀이(2) (0) | 2022.08.01 |
| FDM #5, Heat Equation의 풀이(1) (0) | 2022.07.30 |
| 미분방정식을 연립방정식으로, FDM #4 (2계 상미분방정식) (0) | 2022.07.25 |




댓글