이 글은
2022.07.25 - [수학의 재미/아름다운 이론] - 미분방정식을 연립방정식으로, FDM #3 (2계 상미분방정식)
미분방정식을 연립방정식으로, FDM #3 (2계 상미분방정식)
이 글은 2022.07.22 - [수학의 재미/아름다운 이론] - 미분방정식을 연립방정식으로, FDM #2 미분방정식을 연립방정식으로, FDM #2 이번 글은 2022.07.22 - [수학의 재미/아름다운 이론] - 미분방정식을 연립
sine-qua-none.tistory.com
에서 이어집니다. 위 글에서는 2계도함수가 포함된 미분 방정식을 FDM으로 푸는 해법을 이론적으로 알아보았습니다.
복습
$x$의 범위를 $0\leq x\leq1$로 하는 미분방정식
$$ f''(x) + p f'(x) + q f(x)= 0~,~ f(0)=y_0 , f(1) = y_1 \tag{1}$$
을 FDM으로 풀기 위해
1. $x$의 범위를 grid로 분할
$x$의 최댓값을 $x_{\max}$라 했을 때, $[0, x_{\max}]$을 $N$등분을 하여
$$ 0=x_0 < x_1 <x_2 <\cdots < x_{N-1} < x_N = x_{\max}$$
의 총 $N+1$개의 $x$ 수열로 격자를 생성합니다.
2. tridiagonal matrix로 행렬 방정식을 세움
계수를
| forward difference | backward difference |
| $$ \begin{align} a_{i} &= \frac1{h^2} \\ b_i & = -\left( \frac2{h^2} + \frac{p}h -q \right) \\ c_i &= \frac1{h^2} +\frac{p}h \end{align} $$ |
$$ \begin{align} a_{i} &= \frac1{h^2} \\ b_i & = -\left( \frac2{h^2} + \frac{p}h \right) \\ c_i &= \frac1{h^2} +\frac{p}h + q \end{align} $$ |
라 했을 때,
$$
\pmatrix
{
b_1 & c_1 & & & &\\
a_2 & b_2 & c_2 & & &\\
& a_3 & b_3 &\ddots & &\\
& & &\ddots & \ddots & \\
& & & a_{N-2} & b_{N-2} & c_{N-2} \\
& & & & a_{N-1} & b_{N-1}
}
\pmatrix
{
u_1 \\
u_2 \\
u_3 \\
\vdots \\
u_{N-2} \\
u_{N-1}
}
=
\pmatrix
{
-a_1 y_0 \\
0\\
0\\
\vdots\\
0\\
- c_{N-1} y_1
}
$$
행렬을 차례대로 $\mathbf{T, u, k}$ 라 하면
$$ \mathbf{Tu} = \mathbf{k} \tag{2}$$
를 푸는 문제로 바뀝니다.
3. 행렬의 계산
식(2)에서
$$ \mathbf{u} = \mathbf{T}^{-1} \mathbf{k}$$
로 $\mathbf{u}$를 구합니다.
Python으로 풀어보기
forward difference 방법이나, backward method 방법이나 tridiagonal의 원소만 조금 바뀔 뿐이지 내용은 똑같으므로 forward difference의 방법으로 설명하겠습니다.
def second_ode_test_explicit():
# solve:
# f''(x) + p f'(x) + q =0 , f(0)=y0, f(1)= y1
p, q = 4, 1
y0, y1 = 1, 1
disc = p ** 2 - 4 * q
Nsteps = 100
x = np.linspace(0, 1, Nsteps + 1)
if disc > 0:
a1 = (-p + np.sqrt(disc)) / 2
a2 = (-p - np.sqrt(disc)) / 2
f1 = np.exp(a1 * x)
f2 = np.exp(a2 * x)
c1 = (np.exp(a2) * y0 - y1) / (np.exp(a2) - np.exp(a1))
c2 = (-np.exp(a1) * y0 + y1) / (np.exp(a2) - np.exp(a1))
y_exact = c1 * f1 + c2 * f2
elif disc == 0:
a = -p / 2
f1 = np.exp(a * x)
f2 = x * np.exp(a * x)
c1 = y0
c2 = y1 * np.exp(-a) - y0
y_exact = c1 * f1 + c2 * f2
else:
z1 = -p / 2
z2 = np.sqrt(-disc) / 2
f1 = np.exp(z1 * x) * np.cos(z2 * x)
f2 = np.exp(z1 * x) * np.sin(z2 * x)
c1 = y0
c2 = y1 / (np.exp(z1) * np.sin(z2)) - y0 / np.tan(z2)
y_exact = c1 * f1 + c2 * f2
##### FDM ##################
nMesh = [5, 10, 50, 100, 1000]
for i in range(len(nMesh)):
xgrid = np.linspace(0, 1, nMesh[i] + 1)
h = xgrid[1] - xgrid[0]
u = np.zeros(nMesh[i] + 1)
T = np.zeros((nMesh[i] - 1, nMesh[i] - 1))
for j in range(nMesh[i] - 1):
T[j, j] = -(2 / h ** 2 + p / h - q)
if j + 1 < nMesh[i] - 1:
T[j + 1, j] = 1 / h ** 2
T[j, j + 1] = 1 / h ** 2 + p / h
known = np.zeros(nMesh[i] - 1)
known[0] = -1 / h ** 2 * y0
known[-1] = -(1 / h ** 2 + p / h) * y1
u[1:nMesh[i]] = np.linalg.inv(T) @ known
u[0], u[nMesh[i]] = y0, y1
plt.plot(xgrid, u, marker='.', label='{} grid'.format(nMesh[i]))
plt.plot(x, y_exact, marker='o', label='exact function')
plt.legend()
plt.title('p={}, q={}, p^2-4q ={}'.format(p, q, disc))
plt.show()
if __name__ == '__main__':
second_ode_test_explicit()
code를 간략히 설명하겠습니다.
p, q = 4, 1 # 미분방정식의 계수 세팅
y0, y1 = 1, 1 # x=0 일 때, x=1일 때 초기값 세팅
disc = p ** 2 - 4 * q # 판별식 계산
Nsteps = 100
x = np.linspace(0, 1, Nsteps + 1) #exact solution을 그리기(plotting) 위해 x좌표 격자화 if disc > 0: #판별식이 0보다 크면, x^2+px+q=0의 두근 a1, a2에 대해 e^{a1 x}, e^{a2 x} 가 두 해
a1 = (-p + np.sqrt(disc)) / 2
a2 = (-p - np.sqrt(disc)) / 2
f1 = np.exp(a1 * x)
f2 = np.exp(a2 * x)
c1 = (np.exp(a2) * y0 - y1) / (np.exp(a2) - np.exp(a1))
c2 = (-np.exp(a1) * y0 + y1) / (np.exp(a2) - np.exp(a1))
y_exact = c1 * f1 + c2 * f2 #판별식이 0보다 클 때 exact solution○ 저번 글을 참고하시면 됩니다.
elif disc == 0: #판별식이 0일 떄는 중근 a가 나오고, e^{ax}와 xe^{ax}가 미분방정식의 두 해
a = -p / 2
f1 = np.exp(a * x)
f2 = x * np.exp(a * x)
c1 = y0
c2 = y1 * np.exp(-a) - y0
y_exact = c1 * f1 + c2 * f2 #exact solution○ 저번 글을 참고하시면 됩니다.
else:
# 판별식<0인 경우로 근을 z1+z2i 라 하면
# e^{z1x} cos(z2 x) 와 e^{z1x}sin(z2 x)가 미분방정식의 두 근임
z1 = -p / 2 #근의 실수부
z2 = np.sqrt(-disc) / 2 #근의 허수부
f1 = np.exp(z1 * x) * np.cos(z2 * x)
f2 = np.exp(z1 * x) * np.sin(z2 * x)
c1 = y0
c2 = y1 / (np.exp(z1) * np.sin(z2)) - y0 / np.tan(z2)
y_exact = c1 * f1 + c2 * f2 #exact solution○ 저번 글을 참고하시면 됩니다.
nMesh = [5, 10, 50, 100, 1000]
#x의 격자를 각각 5, 10, 50, 100, 1000 잘게 쪼개가면서 exact solution에 수렴하는 볼 예정
for i in range(len(nMesh)): #격자수를 nMesh list에서 선택하여
xgrid = np.linspace(0, 1, nMesh[i] + 1) #0,1사이를 선택한 nMesh 개만큼 나누고
h = xgrid[1] - xgrid[0] #각 격자의 간격을 h라고 둠
u = np.zeros(nMesh[i] + 1) # xgrid에 nMesh+1 개의 점이 있으므로 FDM 결과인 u도 nMesh+1 size로 설정함
T = np.zeros((nMesh[i] - 1, nMesh[i] - 1)) #tridiagonal을 끝점 두 개 뺀 nMesh-1 정방행렬로 구성
for j in range(nMesh[i] - 1):
T[j, j] = -(2 / h ** 2 + p / h - q) # 대각선의 b_i 계수 대입
if j + 1 < nMesh[i] - 1:
T[j + 1, j] = 1 / h ** 2 # 대각선 바로 아래 a_i 계수 대입
T[j, j + 1] = 1 / h ** 2 + p / h # 대각선 바로 위에 c_i 계수 대입
known = np.zeros(nMesh[i] - 1) # 행렬방정식의 우변행렬
known[0] = -1 / h ** 2 * y0 # 첫째원소 조정(지난글)
known[-1] = -(1 / h ** 2 + p / h) * y1 # 마지막원소 조정(지난글 참조)
u[1:nMesh[i]] = np.linalg.inv(T) @ known #u[1]~u[nMesh[i]-1] 까지가 Tu =k 를 만족하므로
u[0], u[nMesh[i]] = y0, y1 #u[0]와 u[nMesh[i]]는 boudary condition으로 따로 지정
결과
1. $p^2 -4q>0$일 때,
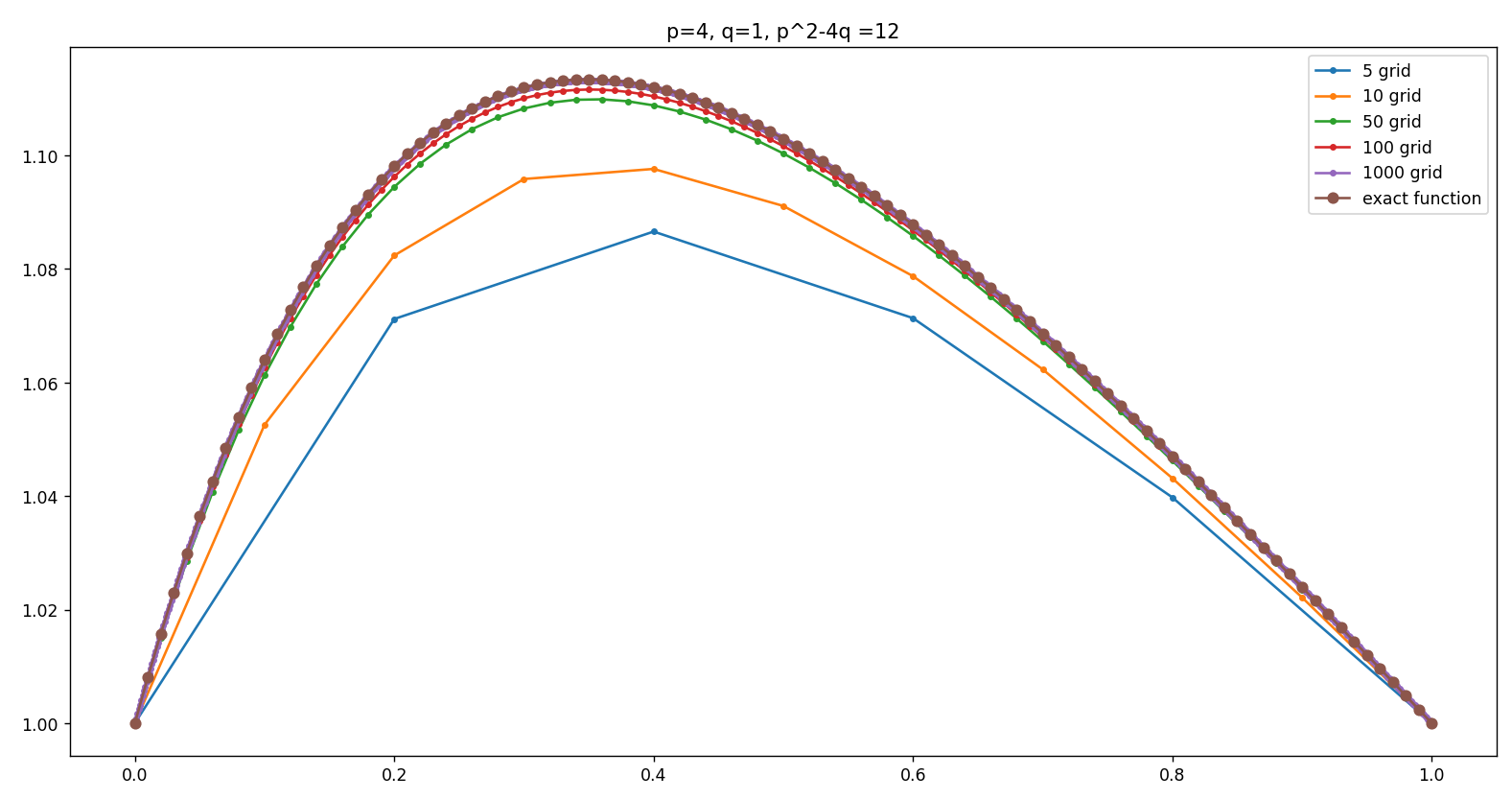
그리드를 잘게 쪼갤수록 exact solution에 수렴하는 것이 보입니다.
2. $p^2 -4q =0$일 때,

2. $p^2 -4q <0$일 때,
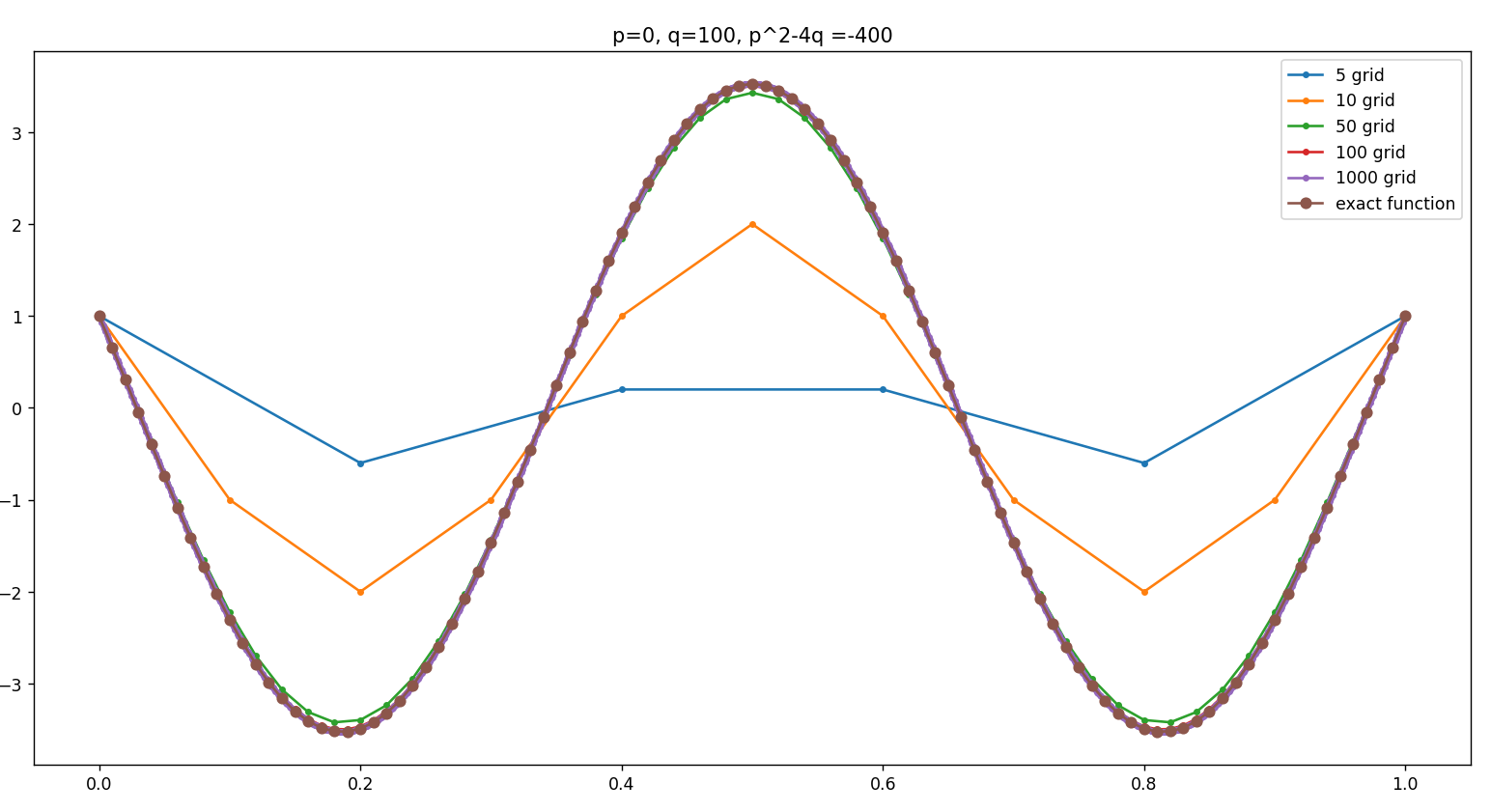
근이 복소수가 나올 땐 $\sin, \cos$의 1차 결합으로 해가 표시되는데, 차트를 통해서도 확인할 수 있습니다.
지금까지는 하나의 변수에 대한 2계 상미분방정식을 FDM으로 어떻게 다루는지 알아보았습니다. 하지만 많은 미분방정식이 사실 2 변수 이상의 함수에 대한 편미분 방정식으로 주어져 있죠. 편미분 방정식은 FDM으로 어떻게 해결할 수 있는지 다음 글에서 알아보도록 하겠습니다.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| FDM #6, Heat Equation의 풀이(2) (0) | 2022.08.01 |
|---|---|
| FDM #5, Heat Equation의 풀이(1) (0) | 2022.07.30 |
| 미분방정식을 연립방정식으로, FDM #3 (2계 상미분방정식) (1) | 2022.07.25 |
| 미분방정식을 연립방정식으로, FDM #2 (0) | 2022.07.22 |
| 미분방정식을 연립방정식으로, FDM #1 (0) | 2022.07.22 |



댓글