이 글은
2022.07.30 - [수학의 재미/아름다운 이론] - FDM #5, Heat Equation의 풀이(1)
FDM #5, Heat Equation의 풀이(1)
이번 글은 2022.07.25 - [수학의 재미/아름다운 이론] - 미분방정식을 연립방정식으로, FDM #4 (2계 상미분방정식) 미분방정식을 연립방정식으로, FDM #4 (2계 상미분방정식) 이 글은 2022.07.25 - [수학의 재
sine-qua-none.tistory.com
에서 이어집니다.
열방정식의 예시
저번 글에서 다루었던 예시는 다음과 같습니다.
ut(t,x)=uxx(t,x),0<x<1,t>0, tag1
○ 초기 조건: u(0,x)=sin(πx)
○ 경계조건: u(t,0)=u(t,1)=0
※ 참고 이 방정식의 exact solution 은
u(t,x)=sin(πx)exp(−π2t)
이산화 과정
저번 글에서 알아보았듯이 시점 변수 t와 변위 변수 x를 다음과 같이 격자로 나눕니다.
열방정식의 이산화 과정
1. 시간 t 축을 유한개의 균등 격자로 나눔
- 식(1)에는 초기시점 t=0은 있지만, 끝시점은 없죠. 따라서 관심 있는 충분히 큰 끝시점 T를 하나 정하고,
0=t0<t1<t2<⋯<tN−1<tN=T
로 균등하게 나눔
- 각 시점의 차이는 k로 일정함. 즉, tn+1−tn=k
2. 변위 변수 x도 유한개의 균등 격자로 나눔
- 식(1)의 x가 움직이는 구간을 [xm,xM]이라 했을 때,
xm=x0<x1<x2<⋯<xJ−1<xJ=xM
으로 균등하게 나눔
- 각 변위의 차이는 h로 일정함. 즉, uj+1−uj=h
이제 (t,x)를 격자를 사용하여 편미분 방정식을 연립방정식으로 만들어 보겠습니다.
FDM 설계를 위한 예비 지식
FDM을 설계하기 위한 예비 지식은
2022.07.22 - [수학의 재미/아름다운 이론] - 미분방정식을 연립방정식으로, FDM #1
미분방정식을 연립방정식으로, FDM #1
이번 글에서는 미분방정식을 해결하는 방법을 소개합니다. 수많은 자연현상, 경제 현상, 사회 현상 등 변화와 상태를 연결 짓는 고리가 미분방정식으로 표현되는 경우가 너무나 많고, 이러한 방
sine-qua-none.tistory.com
을 참고하시면 됩니다. 기본적으로 foward difference, backward difference, central difference를 알고 있으면 됩니다.
FDM 설계
이제 (t,x)를 격자를 사용하여 편미분 방정식을 연립방정식으로 만들어 보겠습니다.
0=t0<t1<⋯<tn=T와
xm=x0<x1<⋯<xJ=xM
에 대해 식(1)을 아래의 방법으로 이산화 시킵니다. t 수열 사이 간격은 k, x수열 사이 간격은 h입니다.
시점 tn에서 forward difference 방식으로 이산화 시키자!
그러면 점 (tn,xj)에서 k 만큼의 시점 차로 forward difference를 구하면
ut(tn,xj)=u(tn+k,xj)−u(tn,xj)k이고
tn+k=tn+1입니다.
이제
unj=u(tn,xj)
라 정의하면
ut(tn,xj)=un+1j−unjk
이죠. x에 대해서는 central difference를 사용합니다. x의 차이를 h라 하면
uxx(tn,xj)=u(tn,xj+h)−2u(tn,xj)+u(tn,xj−h)h2
입니다. xj±h=xj±1 이므로 준식은
uxx(tn,xj)=unj+1−2unj+unj−1h2
따라서 ut(t,x)=uxx(t,x)는 식(2), (3)을 결합하여 다음과 같이 변합니다.
un+1j−unjk=unj+1−2unj+unj−1h2
α=kh2 이라 하면
un+1j−unj=α(unj+1−2unj+unj−1)
정리하면
un+1j=αunj+1+(1−2α)unj+αunj−1
식(*)가 바로 식(1)을 이산화 시킨, FDM의 주요 부위가 됩니다. 글로 해석을 하자면,
n step에 있는 j−1,j,j+1 번째 값 3개를 가지고 n+1 step의 j번째 값을 구할 수 있다.
라는 거죠. 그림으로 표현하면 이렇습니다.

다시 문제로 돌아가 이번에는 초기 조건을 건드려 봅시다. 초기 조건은
u(0,x)=sin(πx)
이죠 이산화 하면, 모든 j에 대해
u(t0,xj)=sin(πxj)
즉,
u0j=sin(πxj),∀j
입니다.
경계조건에서 모든 n에 대해
u(tn,x0)=0 , u(tn,xJ)=0
즉,
un0=0 , unJ=0,∀n
입니다.
이제 세팅은 다 끝났습니다. 모든 격자를 구하는 과정을 정리하면 아래 그림과 같지요.
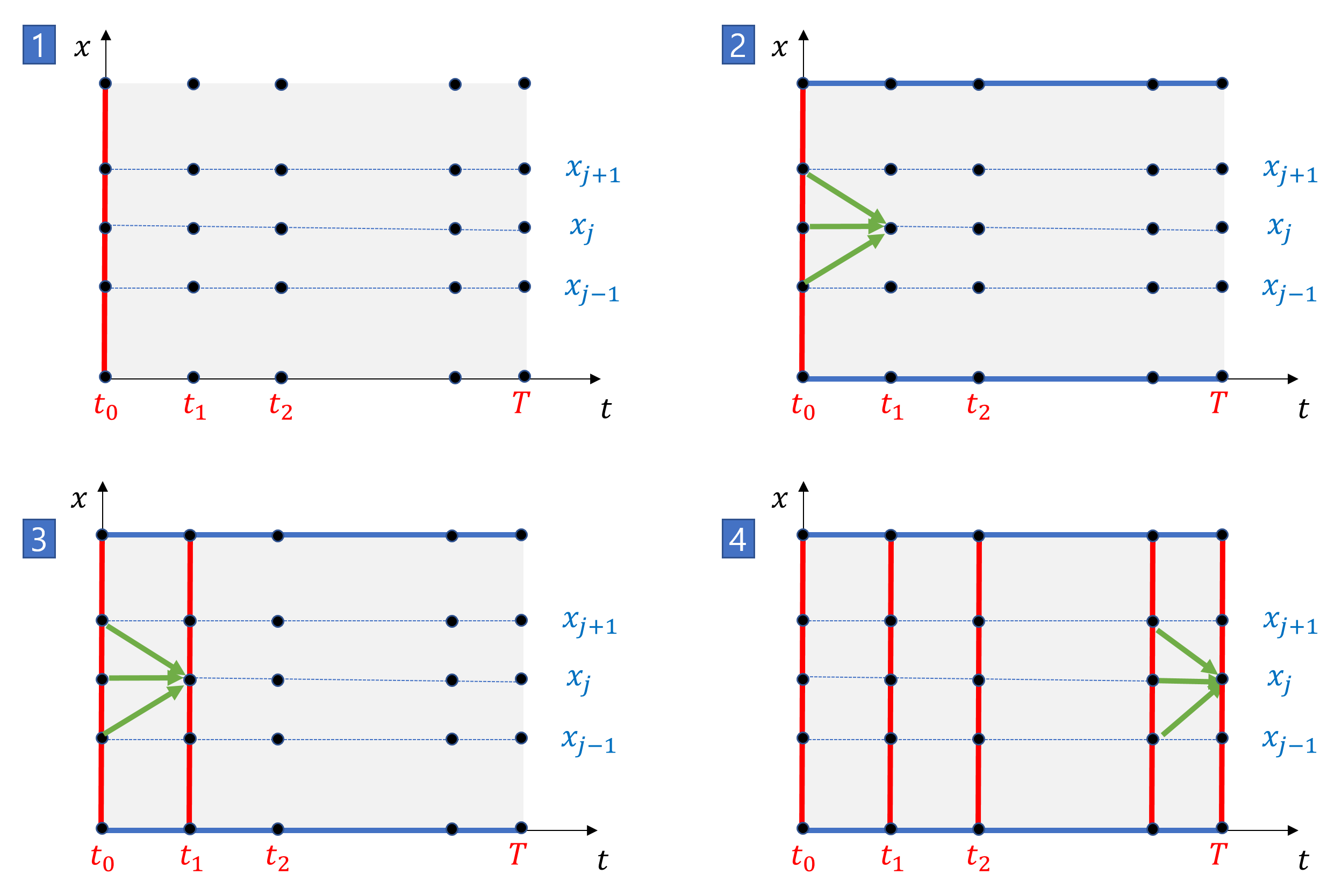
1. 초기 조건을 이용하여 t0의 모든 격자에 값을 부여함 (빨간색 선)
2. 경계조건을 이용하여 x0,xJ의 모든 격자에 값을 부여함(파란색 선)
3. 점화식 (*)을 이용하여 t1의 모든 격자점의 값 구함
4. tN까지 모든 격자점의 값을 구함
FDM 코드
python으로 작성한 위 문제의 FDM 풀이법은 다음과 같습니다.
def Solve_HeatEqaution_1D_explicit():
# u_t(t,x) = u_xx(t,x) 0<x<1, t>0
# u(0,x) = sin(πx)
# u(t,0)= u(t,1) =0
# closed form solution : u(t,x)= sin(πx)exp(-π^2 t)
x_min, x_max = 0, 1
t0 = 0
maturity = 1
num_x, num_t = 50, 10000
# num_x, num_t = 50, 4500
# num_x, num_t = 70, 10000
# num_x, num_t = 80, 10000
x_seq = np.linspace(x_min, x_max, num_x + 1)
t_seq = np.linspace(t0, maturity, num_t + 1)
h = x_seq[1] - x_seq[0]
k = t_seq[1] - t_seq[0]
alpha = k / h ** 2
print('delta of x : {:.3f}'.format(k))
print('delta of t : {:.3f}'.format(h))
print('alpha (= k/(h^2)) : {:.3f}'.format(alpha))
u = np.empty((num_t + 1, num_x + 1))
# print(u)
# u(t,x_min) =0
u[:, 0] = 0
# u(t, x_max) =0
u[:, -1] = 0
# u(0, x) = sin( pi*x)
u[0, :] = np.sin(np.pi * x_seq)
for n in range(0, num_t):
for j in range(1, num_x):
u[n + 1, j] = u[n, j] + alpha * (u[n, j + 1] - 2 * u[n, j] + u[n, j - 1])
real_t = t_seq[-1]
sol = np.sin(np.pi * x_seq) * np.exp(-np.pi * np.pi * real_t)
fdm_sol = u[-1, :]
max_of_difference = np.max(sol - fdm_sol)
print('max distance between exact solution and fdm solution is {:.4f}'.format(max_of_difference))
print()
plt.plot(x_seq, sol, 'b', label='exact solution')
plt.plot(x_seq, fdm_sol, 'm', label='fdm solution')
plt.legend()
plt.title('when h={:.3f}, k={:.3f}, alpha={:.3f}'.format(h, k, alpha))
plt.show()
코드의 주요 부분을 간략히 살펴보면,
num_x, num_t = 50, 10000 # 아래 주석처리한 경우까지 포함하여 4가지 경우 테스트 해 볼 격자 구성
# num_x, num_t = 50, 4500
# num_x, num_t = 70, 10000
# num_x, num_t = 80, 10000 x_seq = np.linspace(x_min, x_max, num_x + 1) #[x_min, x_max를 num_x 개의 구간으로 분해
t_seq = np.linspace(t0, maturity, num_t + 1) #[t0, maturity]를 num_t개의 구간으로 분해
#numpy.linspace의 정의상 +1씩 해 줘야 구간의 갯수를 num_x, num_t로 맞출 수 있음
h = x_seq[1] - x_seq[0] #x_seq의 한구간의 길이
k = t_seq[1] - t_seq[0] #t_seq의 한 구간의 길이
alpha = k / h ** 2 #식(*)의 alpha 계산 u = np.empty((num_t + 1, num_x + 1)) # FDM 결과를 담을 격자판 정의
# u(t,x_min) =0
u[:, 0] = 0 # boundary condition
# u(t, x_max) =0
u[:, -1] = 0 # boundary condition
# u(0, x) = sin( pi*x)
u[0, :] = np.sin(np.pi * x_seq) #initial condition
# 식(*)를 이용하여 u의 모든 격자 채우기
for n in range(0, num_t):
for j in range(1, num_x):
u[n + 1, j] = u[n, j] + alpha * (u[n, j + 1] - 2 * u[n, j] + u[n, j - 1]) real_t = t_seq[-1] # t_seq의 가장 마지막 원소 즉, maturity를 의미
sol = np.sin(np.pi * x_seq) * np.exp(-np.pi * np.pi * real_t) # real_t에서의 exact solution
fdm_sol = u[-1, :] # real_t에서의 u의 값들, 즉, FDM solution
max_of_difference = np.max(sol - fdm_sol) #exact solution과 u 값의 비교
결과
결과는 다음과 같습니다. 다음의 4가지 경우를 살펴본다 했습니다.
1. num_x, num_t = 50, 10000 일 때
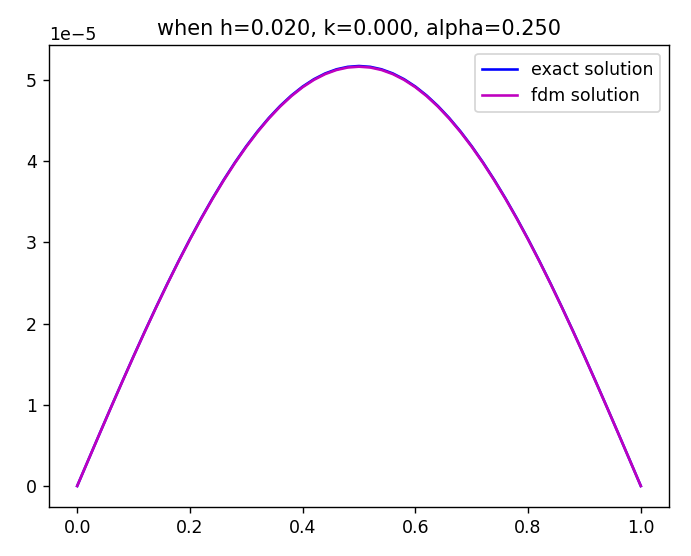
delta of x : 0.000
delta of t : 0.020
alpha (= k/(h^2)) : 0.250
max distance between exact solution and fdm solution is 0.0000
아주 잘 구해진 결과이죠.
2. num_x, num_t = 50, 4500 일 때,
delta of x : 0.000
delta of t : 0.020
alpha (= k/(h^2)) : 0.556
C:\Users\kimju\PycharmProjects\StockProject\fdm_Example.py:288: RuntimeWarning: overflow encountered in double_scalars
u[n + 1, j] = u[n, j] + alpha * (u[n, j + 1] - 2 * u[n, j] + u[n, j - 1])
C:\Users\kimju\PycharmProjects\StockProject\fdm_Example.py:288: RuntimeWarning: invalid value encountered in double_scalars
u[n + 1, j] = u[n, j] + alpha * (u[n, j + 1] - 2 * u[n, j] + u[n, j - 1])
max distance between exact solution and fdm solution is nan아예 계산이 overflow가 나고 있습니다.
3. num_x, num_t = 70, 10000 일 때,
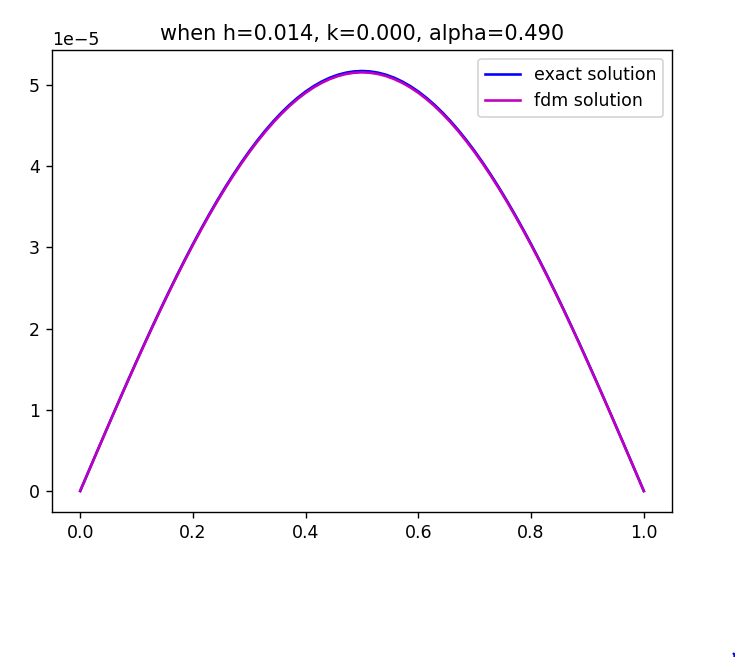
delta of x : 0.000
delta of t : 0.014
alpha (= k/(h^2)) : 0.490
max distance between exact solution and fdm solution is 0.0000아주 좋은 결과를 얻습니다. 마지막으로
4. num_x, num_t = 80, 10000 일 때,
delta of x : 0.000
delta of t : 0.013
alpha (= k/(h^2)) : 0.640
C:\Users\kimju\PycharmProjects\StockProject\fdm_Example.py:288: RuntimeWarning: overflow encountered in double_scalars
u[n + 1, j] = u[n, j] + alpha * (u[n, j + 1] - 2 * u[n, j] + u[n, j - 1])
C:\Users\kimju\PycharmProjects\StockProject\fdm_Example.py:288: RuntimeWarning: invalid value encountered in double_scalars
u[n + 1, j] = u[n, j] + alpha * (u[n, j + 1] - 2 * u[n, j] + u[n, j - 1])
max distance between exact solution and fdm solution is nan아예 또 계산이 안되네요.
결론
위와 같이
- 시점에 대한 forward difference를 써서
- 시점 n의 3개의 점으로 시점 n+1 의 1개의 점을 산출하는 방법을
명시적 방법(explicit method)이라 합니다.
이 방법은 계산이 극히 단순하다는 장점이 있습니다. 하지만 위의 결과처럼 어떤 경우는 결과가 잘 나오고, 어떤 경우에는 아예 계산이 뻑나죠. 결론부터 말하면
α=kh2
이 어떤 값을 가지느냐에 따라 결정됩니다. 구체적으로
α<0.5 이면 명시적 방법의 FDM은 잘 수렴하여 exact solution가 일치합니다. 반면, α>0.5이면 위 예제처럼 계산이 overflow 즉, 계산의 결과가 증폭되며 수렴하지 않는 경우가 발생하죠. 따라서 시점과 변위의 격자 간격은 k,h를 잘 잘라줘야 합니다.
하지만 이런 제약 때문에 우리가 원하는 대로 격자판을 구성할 수가 없게 될 수도 있죠. 또한 무심코 잘나서 α값을 확인 안 했을 때는 어떠한 잘못된 결과가 나올지도 모를 일입니다.
이러한 제약을 해결하고자 FDM의 다른 방법이 발전됩니다. 바로 implicit formula라는 건데, 이에 대해서는 다음 글에서 설명하도록 하겠습니다.
'수학의 재미 > 아름다운 이론' 카테고리의 다른 글
| 주성분 분석(Principal Component Analysis)이란? (2) | 2022.09.02 |
|---|---|
| FDM #7, Heat Equation의 풀이(3) (0) | 2022.08.01 |
| FDM #5, Heat Equation의 풀이(1) (0) | 2022.07.30 |
| 미분방정식을 연립방정식으로, FDM #4 (2계 상미분방정식) (0) | 2022.07.25 |
| 미분방정식을 연립방정식으로, FDM #3 (2계 상미분방정식) (1) | 2022.07.25 |




댓글