이 글은 두드림 ELS? Do Dream? 2X 드림!
두드림 ELS? Do Dream? 2X 드림!
신한투자증권에서 ELS 신상품을 공모 청약한다 해서 살펴봤습니다. ELS이름이 두드림 ELS인데요. 뭔가 이름에서 수익을 더블로(2X) 고객에게 드린다는 뜻으로 보입니다. Do Dream의 한글표기법으로도
sine-qua-none.tistory.com
에서 이어집니다. 저번 글에서는 신한증권투자가 공모 청약 진행중인 두드림 ELS를 소개하고, 과거 주가에 대한 시뮬레이션 결과는 어땠는지 백테스트 해보았습니다.
이제 금융공학적으로 Tesla를 기초자산으로 하는 두드림 ELS의 이론가를 계산해 보도록 하겠습니다.
두드림 ELS
두드림 ELS에는 아래와 같은 구조입니다.

○ 조기상환 시점에 배리어가 넘는지 안넘는지를 판단함
○ 조기상환이 안되면 만기 시점에 오른쪽 그래프처럼 페이오프 산정
딱 보니까 중요한 날이 두 개 있네요. 조기상환 시점과 만기 시점. 따라서 금융공학적으로 주가 패스를 생성할 때 데일리로 모두 생성할 필요가 없고, 해당 두 날짜의 주가만 모델링하면 됩니다.
주가 모델(GBM)
주가 모델은 GBM 모델을 씁니다. 기초자산 $S_t$의 변동성을 $\sigma$, 배당을 $q$, 시장의 무위험 이자율을 $r$이라 할 때,
$$ dS_t/S_t = (r-q)dt+\sigma dW_t,$$
$W_t$는 위너프로세스로서, $W_t\sim \mathcal{N}(0,\sqrt{t}^2)$ 의 분포를 가집니다.
| ※ 여기서 한가지, 위의 두드림 ELS는 기초자산은 달러(USD)를 값으로 움직이고, ELS 자체는 원화(KRW)로 결제가 되는 상품입니다. 이처럼, 기초자산의 통화와 파생상품 자체의 통화가 다른 경우를 콴토 상품이라 합니다. 이 떄, GBM 모델은 그 생김새가 약간 달라집니다. 콴토 상품을 계산하는 GBM 모델이 따로 있거든요. 이것은 차차 설명할 기회를 가지도록 하고, 이 글에서는 마치 Tesla가 원화로 매매할 수 있는 주식이라고 생각하며 이론가를 구해보겠습니다. |
이제 두드림 ELS의 계산 시점을 $t$, 조기상환 시점을 $T_1$, 만기시점을 $T_2$라 합시다. 그러면, GBM 주가패스 만들기 #1: 만기시점 주가만 라는 글에 따라 우선 조기상환 시점의 주가를 생성할 수 있습니다.
$$S_{T_1} = S_t \exp\left( (r-q-\textstyle{\frac12}\sigma^2)(T_1-t) + \sigma\sqrt{T_1-t} \cdot w_1\right)~~, ~~ w_1 \sim \mathcal{N}(0,1)\tag{1}$$
입니다. (1)에서 구한 주가를 조기상환 배리어 $B(=0.85)$와 비교해 봅니다. 조기상환 조건을 만족하면(즉, 주가가 배리어 이상이면) 정해진 쿠폰 $c(=6\%)$ 을 지급하고 끝납니다. 아니라면, (1)에서 구한 $S_{T_1}$에서 출발하여 만기시점 $T_2$에서의 주가
$$ S_{T_2} = S_{T_1} \exp\left( (r-q-\textstyle{\frac12}\sigma^2)(T_2-T_1) + \sigma\sqrt{T_2-T_1} \cdot w_2\right)~~, ~~ w_2 \sim \mathcal{N}(0,1)\tag{2}$$
를 구합니다. 이렇게 구한 주가가 기준가 대비 $1$ 이상일 때,
$$ 2\left(\frac{S_{T_2}}{S_0}-1 \right)$$ 이 수익이고 여기에 원금 1을 더한 금액이 상환금액이 됩니다.
만일 만기 주가가 기준가 대비 $1$ 미만이면
$$ \frac{S_{T_2}}{S_0}-1$$이 손실금액이 되겠고, 여기에 원금 1을 더하여 상환합니다.
GBM 모델을 보면 파라미터 $r, q, \sigma$가 쓰이는 것이 보이죠? 이제 이런 모수들을 구해보도록 합시다.
GBM 모수 구하기
이자율 $r$
앞서 가정한 바와 같이 Tesla를 한국 주식으로 생각하기로 했습니다. 해당 상품 만기가 1년이므로, 그냥 1년짜리 무위험 이자율을 찾아봅시다. 구글링을 해보니 아래처럼 검색이 되네요.

나라에서 발행한 국채를 무위험 자산으로 판단하고 1년 만기 국채에서 이자율을 뽑아낸 것입니다(사실, 만기수익률이냐 현물이자율이냐 꼼꼼히 따져야 하지만, 여기서는 그냥 저 값을 쓰기로 합니다.)
연속배당률 $q$
테슬라가 배당을 줄까요?
찾아볼 것도 없이 테슬라는 배당을 안 하기로 유명합니다. Investing.com에서 조회해 보니 역시나군요. 배당률을 0으로 합니다.
변동성 $\sigma$
변동성은 시장에서 관찰하기 어렵습니다. 테슬라 옵션의 거래가 활발하여 내재변동성을 추출하는 방법이 제일 좋겠지만, 이것도 정확한 답은 아닙니다. 변동성은 이거다! 싶은 답이 없기에 여기서는 비교적 구하기 쉬운 역사적 변동성을 구해보도록 합니다. 아래처럼 python code를 통하여 관찰해 보도록 하죠.
참고로 역사적 변동성 구하는 방법은
글을 참고하시기 바랍니다.
def load_data(stock_code, start_date, end_date):
df = fdr.DataReader(stock_code, start_date, end_date, exchange='NASDAQ')
return df
def cal_vol():
stock_code = 'TSLA' # Tesla code
end_date = datetime.datetime.today() # 조회 종료일
start_date = end_date - relativedelta(years=10) # 조회 시작일(10년전)
df = load_data(stock_code, start_date, end_date) # data load
df['Date'] = df.index
df['Rate'] = (df.Close - df.Close.shift(1)) / df.Close.shift(1) # 일일 수익률 계산
df['Vol250'] = df.Rate.rolling(250).std() * np.sqrt(252) # 250일 역사적 변동성
df['Vol180'] = df.Rate.rolling(180).std() * np.sqrt(252) # 180일 역사적 변동성
df['Vol250_mean'] = df.Vol250.rolling(250).mean() # '250일 변동성의 250일 평균
fig, ax = plt.subplots()
ax1 = ax.twinx()
ax.plot(df.Date, df.Close, color='gray', label='TSLA')
ax1.plot(df.Date, df.Vol250, color='tomato', label='volatility(250)')
ax1.plot(df.Date, df.Vol180, color='darkorange', label='volatility(180)')
ax1.plot(df.Date, df.Vol250_mean, linewidth=5, color='royalblue', label='avg(vol250)')
ax1.scatter(df.Date.iloc[-1], df.Vol250_mean.iloc[-1], marker='o', s=100)
ax1.text(df.Date.iloc[-1], df.Vol250_mean.iloc[-1] * 1.03, 'vol:{:.2f}%'.format(df.Vol250_mean.iloc[-1] * 100),
fontweight='bold', color='blue')
ax.legend(loc='upper right')
ax1.legend(loc='upper left')
fig.suptitle('Tesla Volatility')
plt.show()
결과는 아래와 같습니다.
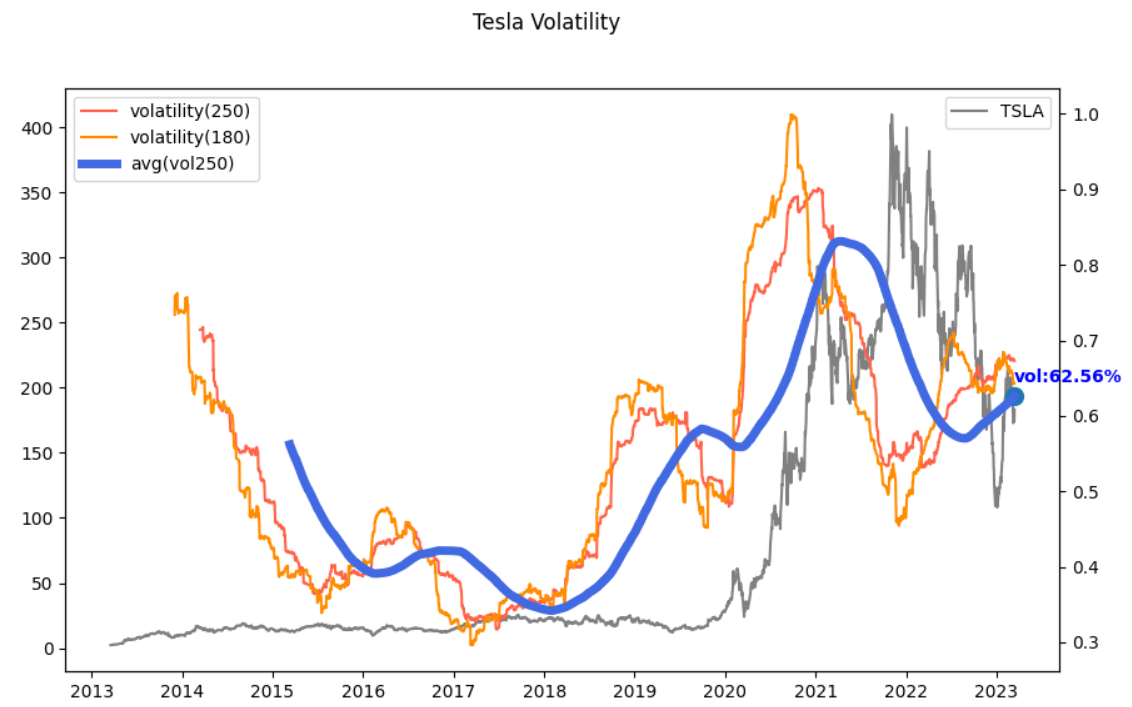
위 그래프 산출 과정은 이렇습니다.
○ 180일 변동성과 250일 변동성을 그려봅니다. 붉은색 그래프 2개입니다. 둘 다 너무 변화가 심합니다.
○ 상대적으로 적은 변동을 보이는 250일 변동성을 스무딩(smooting) 시키기 위해 다시 과거 250개를 평균합니다. 이것이 파란색 그래프입니다.
○ 여전히 변동이 심하지만, 이 정도는 Tesla 주식의 본연의 모습이라 판단하고 가장 최근 변동성 62.56%를 사용합니다.
이제 모수들이 얼추 구해졌습니다.
| 모수 | 값 |
| 이자율 | 3.538% |
| 배당률 | 0% |
| 변동성 | 62.56% |
내용이 길어지므로 두드림 ELS의 이론가는 다음 글에서 이어나가도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 환율은 어떻게 모델링 하나? (0) | 2023.04.19 |
|---|---|
| 두드림 ELS? Do Dream? 2X 드림! : 이론가 계산하기 #2 (0) | 2023.03.16 |
| 두드림 ELS? Do Dream? 2X 드림! (0) | 2023.03.14 |
| 2Star WorstPerform 풋옵션 가격: FDM(OSM) (0) | 2023.02.28 |
| 워스트포퍼머의 기댓값 #2 : Python Code (0) | 2023.01.25 |




댓글