기초자산의 GBM 모델은 위험 중립 측도(risk neutral measure) 하에서 다음과 같이 주어집니다. 기초자산 프로세스를 $S_t$라 하면
$$ dS_t/S_t = (r-q)dt + \sigma dW_t$$
로 주어집니다. 여기서
○ $r$ : 무위험 이자율
○ $q$ : 연속배당률
○ $\sigma$ : 변동성
○ $W_t$ : 위너프로세스로서 $\mathcal{N}(0,\sqrt{t}^2)$ 을 따름
이 중, 변동성은
기초자산이 얼마큼 활발하게 움직이는지를 나타내는 양
으로서, 만일 변동성이 크면 이 기초자산의 등락폭은 커지게 되고, 변동성이 작으면 작을수록 소소한 움직임을 보일 것입니다. 예컨대 KOSPI, KOSPI200 등의 지수 등은 그 등락률이 작고요, 동전주, 세력주, 테마주 등등은 변동성이 커 널뛰기하는 장을 보여줍니다.
2022.05.27 - [금융공학] - 주식의 수학적 모델 #1에서 GBM모델을 설명하며, 변동성을 가볍게 언급한 바 있습니다. 참고하시기 바랍니다.
변동성은 과거의 값인가? 미래를 예측하는 값인가?
금융공학적으로 금융상품의 가격을 계산할 때 쓰이는 변동성은 당연히 미래의 변동성을 예측하여 집어넣어야 합니다. 왜냐하면 금융상품의 가격 계산은
○ 미래의 만기 주가를 모델링(예측)한다.
○ 예측된 주가에 연동된 페이오프(수익/손실)를 계산하여 평균한다.
○ 위 값을 현재가치로 할인한다.
의 단계로 계산하기 때문입니다. 만기 주가를 예측하기 위해서는 현시점부터 미래 시점까지 주가의 움직임이 잘 모델링이 돼야 하는데, 이때 변동성이 결정적인 역할을 합니다.
그런데 문제는
미래의 주가 변동성은 예측하기 불가능하다.
라는 겁니다. 당연한 이야기겠죠. 따라서 주가의 변동성을 구할 때, 지금까지 그 주가가 흘러온 역사를 되돌아봅니다. 지금까지 흘러왔던 대로 주가의 움직임이 연속될 거라는 가정인 거죠.
이처럼, 역사적인 흐름 속에서 산출한 변동성을 역사적 변동성(historical volarility)라고 부릅니다.
이 방법은 변동성을 산출하는 방법 중 쉽고 직관적이라 가장 널리 쓰이는 방법입니다. 다만, 미래를 예측하는 수치는 아닌 거죠.
역사적 변동성 산출 방법
역사적 변동성이란, 단 한 줄로 정의할 수 있습니다.
주식의 최근 일일 등락률의 표준편차
여기서 주의할 점은, 변동성을 얘기할 때는 연간 변동성을 의미하는 것이 컨벤션입니다. 따라서 일일 등락률로 얻은 결과를 연 단위로 환산해 줄 방법도 필요하죠.
주식의 일일 등락률의 정의 방법은 두 가지가 있습니다. 일반 수익률, 로그 수익률인데요. 자세한 내용은 여기를 참고해 보시기 바랍니다. 복습해보면, 오늘의 주가를 $S_t$, 어제의 주가를 $S_{t-1}$이라 하면,
| 구분 | 수식 |
| 일반수익률 | $u_t = (S_t-S_{t-1})/S_{t-1}$ |
| 로그수익률 | $ \ln(S_t/S_{t-1})$ |
역사적 변동성을 구할 때는 일반 수익률이나, 로그 수익률 아무거나 써도 됩니다. 보통은, 우리에게 친숙한 일반 수익률을 씁니다.
방법 I
역사적 변동성을 구하기 위한 정석적인 방법은 아래와 같습니다.
| 오늘의 주가를 $S_t$ 라 하고, 과거의 주가를 어제, 그제 순으로 $$ S_{t-1}, S_{t-2}, \cdots, $$ 라 하자. #1. 시점 $t-i$에서의 일반수익률을 $u_{t-i}$라 하자. 즉, $$ u_{t-i} = \frac{S_{t-i}-S_{t-i-1}}{S_{t-i-1}}$$ #2. 위의 1에서 구한 일반수익률 샘플을 $N$개 모은다. 즉, $$ u_t, u_{t-1} , \cdots, u_{t-N+1}$$ 이 최근 일반수익률 샘플이다. #3. 2에서 구한 샘플들의 표준편차를 구한다. 이것이 바로 주가의 일일 변동성 임 #4. 연변동성을 구하기 위해 $\sqrt{252}$를 3의 결과에 곱한다. |
위의 #4번에서 뜬금없는 숫자 252는 무엇일까요? 바로
1년 동안의 영업일수, 즉 1년간 등장하는 일일 수익률의 개수
입니다. 이는 연마다 다르지만, 통상 1년은 52주이고, 주마다 토/일요일은 주식거래일이 아니므로 104일은 최소 휴장일입니다. 여기에 법정 공휴일, 설/추석 명절, 석가탄신일, 크리스마스에 대체공휴일까지 평균적으로 10일 정도가 더 휴장일인 셈이죠. 따라서 평균적인 영업일은 약 252일 정도가 됩니다.
만일 일일 로그수익률로 연간 등락률을 생각해 보면
$$ \ln(S_t/S_{t-1Y}) = \underbrace{\ln(S_t/S_{t-1})+\cdots +\ln(S_{t-251}/S_{t-252})}_{\text{252 terms}}$$
우변의 252개 항을 독립 사건으로 가정을 하면,
$$ \mathbb{V}(\ln(S_t/S_{t-1Y})) = \underbrace{\mathbb{V}(\ln(S_t/S_{t-1}))+\cdots +\mathbb{V}(\ln(S_{t-251}/S_{t-252}))}_{\text{252 terms}}\tag{1}$$
이제 일일 등락률의 표준편차를 $s$라 하면 식(1)의 우변은 $252s^2$가 되므로
$$ \mathbb{V}(\ln(S_t/S_{t-1Y})) = 252s^2$$
이고 따라서 $ln(S_t/S_{t-1Y})$의 표준편차는
$$\sqrt{252}s$$
입니다. 이런 이유에서 $\sqrt{252}$라는 숫자가 등장하는 것입니다.
비록 로그수익률을 썼을 때를 가정하여 분석했지만, 로그수익률과 일반 수익률은 그 값이 거의 차이가 나지 않으므로 이렇게 설명하고 넘어가겠습니다.
#3에서 표준편차를 구한다고 했죠. 엑셀이나 python 등을 통해 표준편차를 쉽게 구할 수 있습니다만, 표준편차를 구하지 않고 다른 방법으로도 변동성을 구할 수 있습니다. 일반적으로 확률변수 $X$에 대해 $\mathbb{V}(X) = \mathbb{E}(X^2)-\mathbb{E}(X)^2$ 입니다. 그런데 $X$가 주가 수익률처럼 굉장히 작은 값을 가질 경우에는, 또 주가수익률처럼 0근처에서 플러스 마이너스를 띄며 움직이는 변수인 경우에는 $\mathbb{E}(X)^2=0$으로 간주할 수가 있습니다. 즉,
$$\mathbb{V}(X) \approx \mathbb{E}(X^2)$$
인 것이죠.
따라서 아래와 같은 방법으로도 역사적 변동성을 계산할 수 있습니다.
방법 II
| 오늘의 주가를 $S_t$ 라 하고, 과거의 주가를 어제, 그제 순으로 $$ S_{t-1}, S_{t-2}, \cdots, $$ 라 하자. #1. 시점 $t-i$에서의 일반수익률을 $u_{t-i}$라 하자. 즉, $$ u_{t-i} = \frac{S_{t-i}-S_{t-i-1}}{S_{t-i-1}}$$ #2. 위의 1에서 구한 일반수익률 샘플을 $N$개 모은다. 즉, $$ u_t, u_{t-1} , \cdots, u_{t-N+1}$$ 이 최근 일반수익률 샘플이다. #3. 2에서 구한 샘플들을 제곱하여 $N$으로 나눈다. 즉, 샘플의 2차모멘텀(제곱의 기댓값)을 구한다. 그리고 이것을 제곱근한다. #4. 연변동성을 구하기 위해 $\sqrt{252}$를 3의 결과에 곱한다. |
이 방법은 위에서 설명했듯, 주식의 일반 수익률의 기댓값을 0으로 간주하는 방법이죠.
이제 역사적 변동성을 Python으로 구해보겠습니다.
Python Code
import yfinance as yf # KOSPI지수 데이터를 yahoo finance를 이용하여 불러올수 있는 모듈
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
year_scaler = np.sqrt(252) #일간 변동성을 연변동성으로 바꿀 팩터
index_name = '^KS11' #yahoo finance에서 제공하는 KOSPI 의 ticker
df_index = yf.download(index_name, start="2000-01-01", end="2022-11-01")
# KOSPI 데이터를 2000년 초부터 2022/11/01미만일까지 load
df = df_index[['Close']].copy() #불러온 데이터에서 종가(Close) features만 따로 추출
df['rate'] = (df.Close - df.Close.shift(1)) / df.Close.shift(1)
# shift 함수를 사용하여 일일 일반수익률 계산하여 rate
####### 역사적 변동성 계산 첫 번째 방법 ######
vol_days = 180 # 표준편차를 구하기 위한 샘플 갯수
df['vol'] = year_scaler * df['rate'].rolling(window=vol_days).std()
# df의 rate 컬럼 필드에서 기준row의 위쪽으로 vol_days만큼의 data를 선택하는 rolling calculation
# vol_days 만큼의 데이터를 선택하여 표준편차를 구함 (.std())
# 이 값을 vol 이라는 새로운 column을 만들어 저장
# year_scaler를 곱하여 연변동성 구함
####### 역사적 변동성 계산 두 번째 방법 ######
df['rate_square'] = df['rate'] * df['rate']
# rate_square라는 새로운 column 생성하여, rate^2 을 계산하여 대입
df['vol2'] = year_scaler * (df['rate_square'].rolling(window=vol_days).mean()) ** (0.5)
# rate의 제곱의 합에 제곱근을 취하고 year_scaler를 곱하여 vol2라는 새로운 column에 저장
df = df.dropna()
# N/A 원소가 있는 row를 없앰
# rolling method를 사용할 때, 처음 몇 row에 대해서는 window=180을 잡을 공간이 안나오므로
# 계산이 안됨. 따라서 N/A가 뜨고 이 값을 없앰
fig, ax1 = plt.subplots() #subplots() 함수를 사용하여 ax설계
ax1.plot(df.index, df.vol, color='darkorange', label='historical vol.')
ax1.plot(df.index, df.vol2, color='limegreen', label='historical vol2.')
ax1.legend()
ax2 = ax1.twinx() #같은 축에다 그리기 위해 동일 ax1과 동일한 Axes를 ax2로 설계
ax2.bar(df.index, abs(df['vol'] - df['vol2']), color='royalblue', label='difference vol1& vol2')
# 방법1과 방법2로 계산한 역사적 변동성을 비교하기 위해 abs(df['vol'] - df['vol2']) 값을
# bar chart로 그림
ax2.legend()
plt.show()
간략한 설명은 주석으로 대체하겠습니다. 긴요하게 쓰이는 python 문법은 다음의 것들이 있습니다.
○ dataframe.rolling(window= ) : 기준 row를 대상으로 일정 영역을 잡아 계산할 필요가 있을 때 쓰임(평균, 분산, 최대/최솟값 등 계산 시)
○ dataframe.shift() : 기준 row의 일정 칸 앞/뒤의 데이터와 연계해서 계산할 때(수익률 등)
○ pyplot.subplots : 리턴 값인 figure와 axes를 핸들링하며 여러 개의 차트를 그릴 때
결과를 보겠습니다.
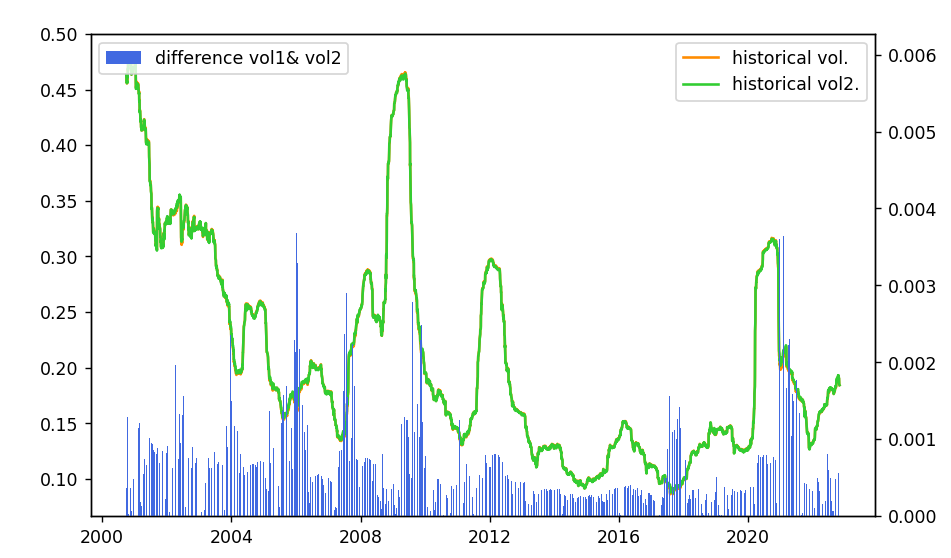
○ 우선 방법 1과 방법 2의 차이를 보시면, 최대 0.4% 정도 보입니다. 즉, 표준편차를 계산하든, 수익률 제곱의 기댓값(2차 모멘텀)을 쓰던 그것은 계산하는 사람의 자유가 되겠습니다.
○ 변동성이 2000년대 초, 2009년 즈음, 2012년 초, 2020년 초 정도에 폭발적으로 증가함을 알 수 있죠. 이때 변동이 커졌다는 뜻은 일일 수익률의 표준편차가 커졌다는 뜻이고, 평소와는 다른 거대한 등락폭이 형성되었다는 뜻인데요, 각각
911 테러, 리먼사태, 미국 신용등급 강등, 코로나19의 원인이 아닐까 싶네요.
○ 위의 그림은 vol_days= 180을 사용한 결과입니다. 이처럼 180개의 샘플을 가지고 구한 역사적 변동성을 180일 변동성이라 합니다. 마찬가지고 60일 변동성, 90일 변동성, 250일 변동성, 500일 변동성 등을 구할 수 있겠죠.
○ 차트를 보니 변동성 변화의 굴곡이 심하네요. 이렇게 변화가 심한 데이터는 시장 상황을 잘 반영하긴 하지만, 이 변동성을 사용하여 얻은 다른 값들, 예를 들어 금융상품의 가격 변화 등이 엄청 심하게 나타날 수밖에 없습니다.
다음 글에서는 $N$일 변동성의 $N$을 좀 조절해 가면서 어떤 특징들을 보이는지를 살펴보겠습니다.
'금융공학' 카테고리의 다른 글
| 기초자산 변동성: EWMA 변동성#1 (0) | 2022.12.06 |
|---|---|
| 기초자산 변동성: 역사적 변동성#2 (0) | 2022.12.01 |
| Brownian Bridge를 이용한 금융상품의 계산 (0) | 2022.11.28 |
| Brownian Bridge: 미래 주가타깃을 정조준하는 주가패스를 만들자. (0) | 2022.11.25 |
| Brownian bridge: 1년뒤 주가타겟을 정조준하는 일일주가의 움직임을 모델링하자 #2 (0) | 2022.11.24 |


댓글