1star 스텝다운 ELS의 계산(FDM) #1

 

 

이 글은 

1star 스텝다운 ELS의 계산(시뮬레이션)과 

2022.12.15 - [금융공학] - 1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지)

1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지)

 에서 이어집니다.  저번 글에서 1star(기초자산 한 개짜리) ELS 가격을 시뮬레이션 기법으로 계산해 봤습니다.

 

ELS 가격을 FDM(Finite Difference Method)으로 구할 수 있습니다. FDM은 크게 

 

○ 명시적 방법 : [수학의 재미/아름다운 이론] - FDM #6, Heat Equation의 풀이(2)

 

○ 함축적 방법 : [수학의 재미/아름다운 이론] - FDM #7, Heat Equation의 풀이(3)

 

이 있습니다. 결과의 안정성을 보장하기 위해서는 함축적 방법(implicit formula)을 쓰는 것이 좋다는 것도 위의 글들을 통하여 알아봤습니다. 

 

 

FDM으로 풀어 본 금융상품의 가격 예제들

 

예전 글들에서 다뤄본 파생상품 중  함축적 FDM 방법으로 풀어본 글들은 다음과 같은 것들이 있습니다.

 

금융상품	참고 글
옵션	옵션 #5. 옵션 프리미엄 구하기 실습: 함축적 FDM
배리어 옵션	배리어옵션 -UOC 옵션 #2 함축적 FDM
디지털 옵션	디지털 옵션 #4. 디지털 옵션 가격, FDM

 

하지만, 위의 3종의 금융상품들은 좀 간단한 구석이 있었죠. ELS와 가장 큰 차이는 바로 만기 때 딱 한번 페이오프가 발생하는 구조라는 거였습니다. 반면에 ELS는

 

○ 낙인 여부에 따라 만기 페이오프가 바뀐다(어디서? full dummy 구간에서)

 

○ 만기뿐 아니라 중간중간에도 조기상환 개념이 있어서 페이오프가 발생한다.

 

라는 특징이 있습니다.  어떻게 FDM을 적용하면 될까요?

 

 

ELS의 FDM 판 설정

 

위에서 언급하였다시피, 

 

① 낙인 배리어를 쳤는지 여부에 따라 페이오프가 달라짐

② 여러 번의 페이오프 발생 기회(예, 3y6m ELS의 경우 총 6번의 상환 기회)가 있음

 

의 특징을 잘 반영해야 합니다. 

- ①을 위해서는 FDM판을 낙인을 안쳤을 때의 격자판(노낙인 격자판),  낙인을 쳤을 때의 격자판(낙인 격자판) 두 개 설정

- ②를 위해서는 time grid가 상환시점과 일치할 때마다 노낙인/낙인 격자판 페이오프를 업데이트시켜줌

- 최종적으로 노낙인 자판, 낙인 격자판을 알맞게 버무려줌

 

의 단계를 거치면 됩니다. 저번 글에서 구해봤던 아래의 상품

 

[그림1] ELS 구조: 3y 6m, 90/90/85/85/80/80, KI 60, coupon 10% p.a.

을 예로 들어 설명해 보겠습니다.

 

낙인 격자판과 노낙인 격자판의 설정

노낙인 격자판, 만기페이오프가 3개로 쪼개진다.

 

낙인 격자판, 만기페이오프가 2개(full dummy 구간 없음) 로 쪼개진다.

 

이제, 노낙인 격자판, 낙인 격자판을 backwardation으로 거꾸로 내려오면서 조기상환 시점들을 만나면 해당 부분에 페이오프를 업데이트해주면 됩니다.

 

 

조기상환 시점 페이오프 업데이트

예컨대 5차 조기상환 시점에서는 아래와 같습니다.

조기상환 5차: 배리어가 80이므로 미리 결정된 붉은 영역중 80이상인 부분을 25%페이오프로 치환해줌

 

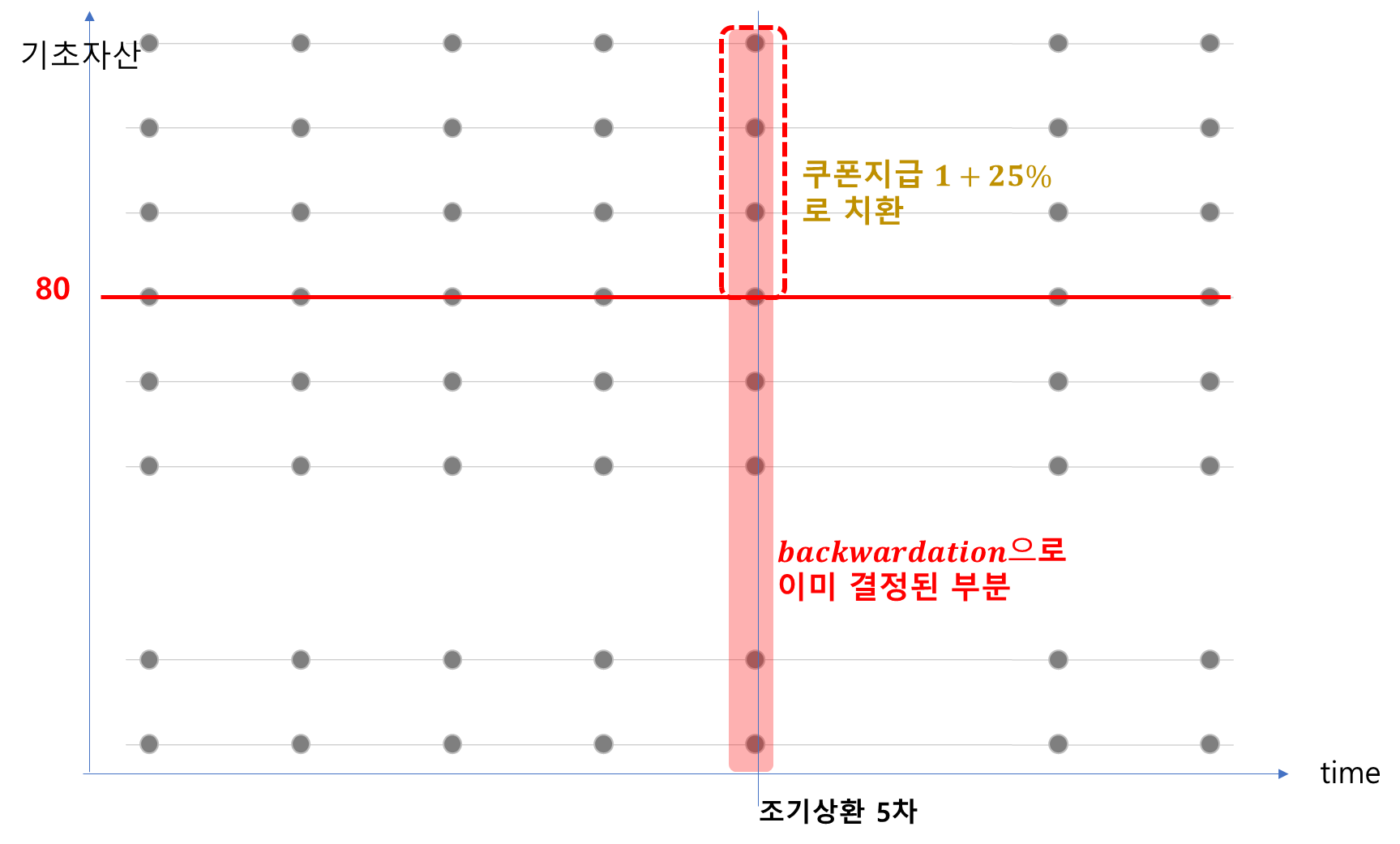
4차 조기상한시점은 배리어가 85이고 쿠폰이 20%이므로 아래와 같습니다.

 

조기상환 4차: 배리어가 85이므로 미리 결정된 붉은 영역중 85이상인 부분을 20%페이오프로 치환해줌

 

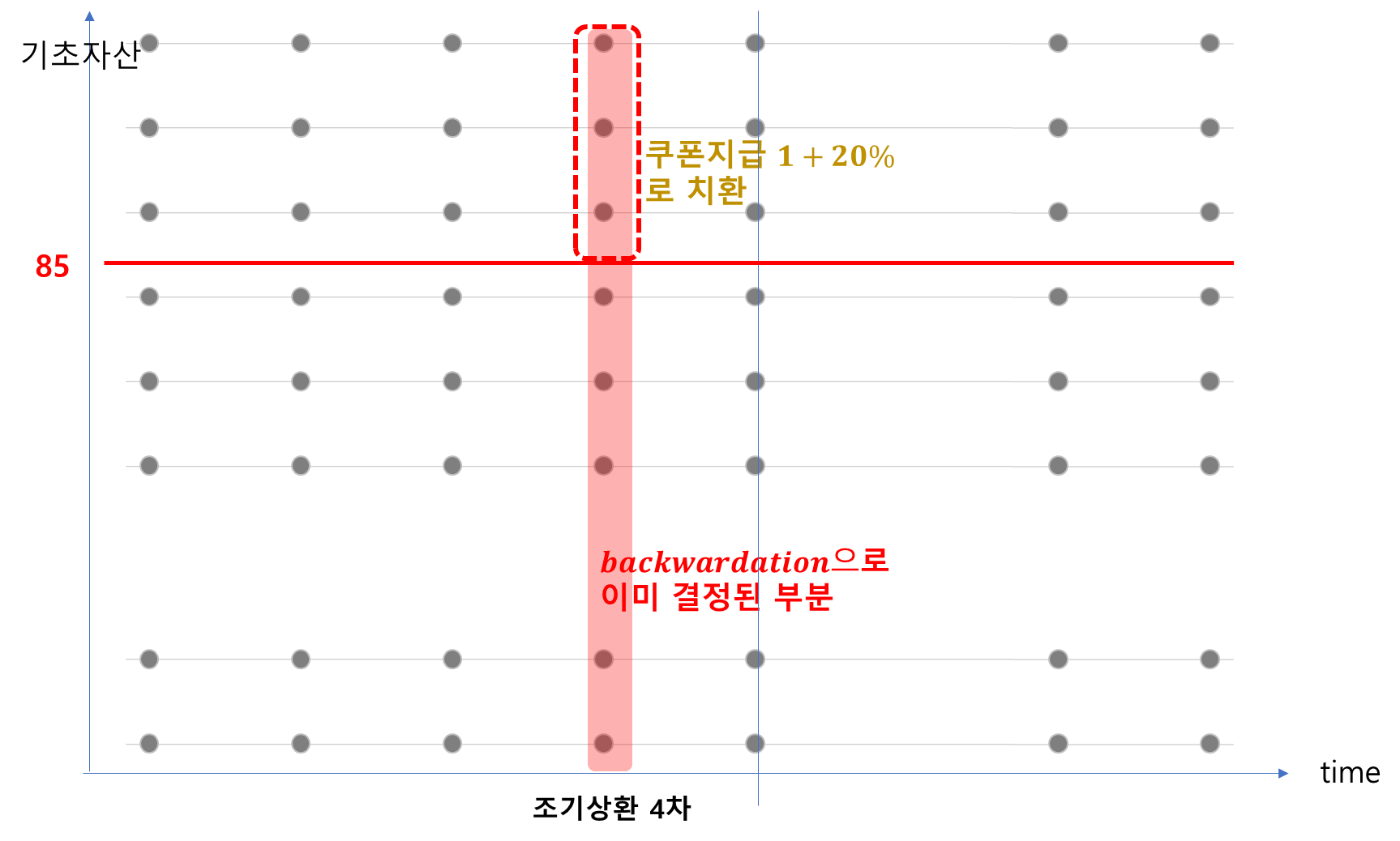
위 과정을 노낙인 격자판, 낙인 격자판에 각각 해주는 것이죠. 1차 조기상환 시점을 거쳐, 시점 0까지요(그림의 제일 왼쪽 격자까지)

 

 

노낙인 격자판, 낙인 격자판 버무리기

위에서 구한 노낙인/낙인 격자판을 최종적으로 한판으로 만들어야 합니다. 노낙인 격자판의 낙인 배리어(60) 미만은 이미 낙인을 친 부분을 함의하므로 낙인 격자판의 값들로 업데이트 쳐주면 됩니다.

이 업데이트는 time grid의 모든 time에 대해서 행해집니다.(조기상환 업데이트는 조기상환시점에만 이루어지는 것과 비교됨)

 

낙인격자판의 KI barrier 밑부분을 노낙인 격자판에 치환하는 방식으로 두 판 버무림

 

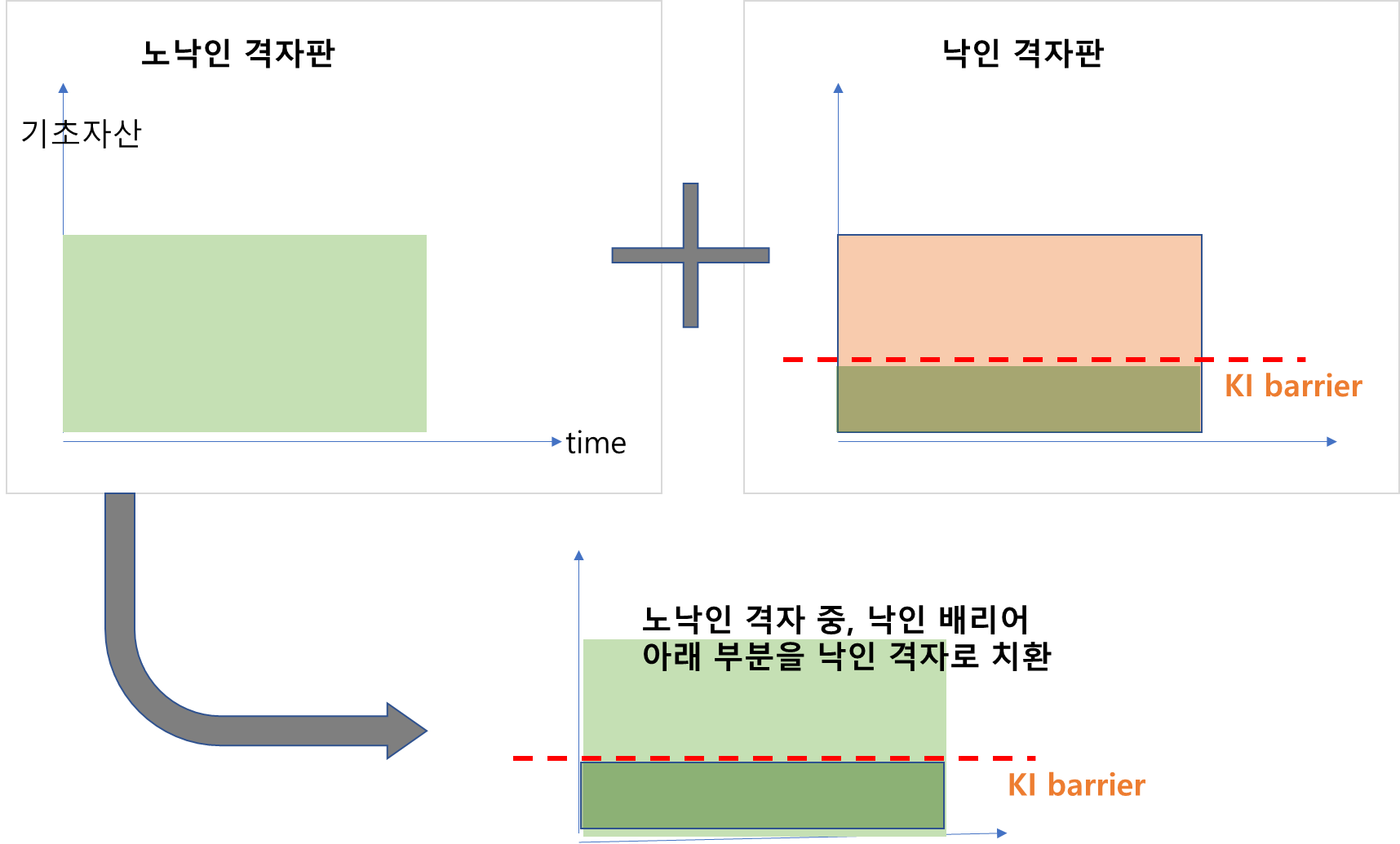
이런 식으로 만기시점부터 현재 시점까지 time grid의 time을 backwardation으로 계산해 내려오면 됩니다.

 

※ 비교: 위의 옵션, 배리어 옵션, 디지털 옵션은 계산 시점 $t$대신 $\tau:T-t$ (여기서 $T$는 만기) 즉, 잔존만기 $\tau$를 기준으로 FDM을 풀기 때문에 

 

만기 페이오프가 초기 조건이 됨

 

을 가정하고 풀었습니다. 하지만 ELS는 직관적인 이해를 높이기 위해 그냥 잔존만기 $\tau$대신 $t$를 사용하고, $t$가 만기시점부터 현시점까지 backwardation으로 진행하는 방법으로 해결해 보도록 하겠습니다.

 

 

 

 

직접적인 코딩은 다음 글에서 진행해 보도록 하겠습니다.