이번 글은
2022.09.01 - [금융공학] - 디지털 옵션 #3. 디지털 옵션 가격, MonteCarlo Simulation
디지털 옵션 #3. 디지털 옵션 가격, MonteCarlo Simulation
지난 글에서는 디지털 옵션의 가격을 Closed Form으로 구해봤습니다. 2022.08.31 - [금융공학] - 디지털 옵션 #2. 디지털 옵션 Closed form 및 그래프 디지털 옵션 #2. 디지털 옵션 Closed form 및 그래프 이번 글
sine-qua-none.tistory.com
에서 이어집니다.
이번 글에서는 디지털 옵션의 가격을 함축적 FDM을 이용하여 구해보겠습니다. 콜옵션이나 UOC 옵션의 FDM 방법과 똑같습니다. 특히 주가 패스의 중간과정에 영향을 받지 않는 콜옵션과 똑같죠. 만기 페이오프는 바꿔주면 됩니다.
FDM 복습(함축적 방법)
FDM은 크게 명시적(explicit) 방법과 함축적(implicit) 방법이 있습니다. 명시적 방법은 계산 알고리즘이 간단하고 빠른 장점이 있지만, 수렴성 문제로 인해 값이 제대로 나오지 않는 경우가 허다했죠. 반면 함축적 방법은 행렬 방정식을 푸는 등 다소 번거로운 작업이 있으나 수렴성 하나만큼은 확실히 보장되는 방법입니다. 따라서 이 글에서는 함축적 방법에 대해서만 다루도록 할게요.
함축적 FDM은
2022.08.01 - [수학의 재미/아름다운 이론] - FDM #7, Heat Equation의 풀이(3)
FDM #7, Heat Equation의 풀이(3)
이 글은 2022.08.01 - [수학의 재미/아름다운 이론] - FDM #6, Heat Equation의 풀이(2) FDM #6, Heat Equation의 풀이(2) 이 글은 2022.07.30 - [수학의 재미/아름다운 이론] - FDM #5, Heat Equation의 풀이(1)..
sine-qua-none.tistory.com
을 참고하면 되고, 이를 이용하여 콜옵션의 프리미엄을 구하는 예제는
2022.08.19 - [금융공학] - 옵션 #5. 옵션 프리미엄 구하기 실습: 함축적 FDM
옵션 #5. 옵션 프리미엄 구하기 실습: 함축적 FDM
지난 글 2022.08.19 - [금융공학] - 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM 저번 글 2022.08.18 - [금융공학] - 옵션 #3. 옵션 프리미엄 구하기(FDM)..
sine-qua-none.tistory.com
을 보면 됩니다.
UOC옵션도 FDM도 계산해 본 적이 있는데요,
2022.08.25 - [금융공학] - 배리어옵션 -UOC 옵션 #2 함축적 FDM
배리어옵션 -UOC 옵션 #2 함축적 FDM
이번 글은 지난 글 2022.08.24 - [금융공학] - 배리어옵션 -UOC 옵션 #1 수학공식(Closed form) 배리어옵션 -UOC 옵션 #1 수학공식(Closed form) 저번 글까지 파생상품의 대표주자 옵션의 프리미엄을 다양한 방
sine-qua-none.tistory.com
를 참고하면 됩니다.
디지털 옵션의 FDM Python Code
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import time
N = norm.cdf
def DigitalOption_FDM_Implicit(s0, strike, upCoupon, downCoupon, maturity, rfr, vol, div):
Nsize, Jsize = 250, 1000
# s variable setting
s_min, s_max = 0, 5 * s0
s_seq = np.linspace(s_min, s_max, Jsize + 1)
h = s_seq[1] - s_seq[0]
# time variable setting
t_min, t_max = 0, maturity
t_seq = np.linspace(t_min, t_max, Nsize + 1)
k = t_seq[1] - t_seq[0]
# solution grid u setting
u = np.empty((Nsize + 1, Jsize + 1))
# initial_condition
u[0, :] = np.array([upCoupon if s >= strike else downCoupon for s in s_seq])
# recursive formula
for n in range(Nsize):
# make tridiagonal matrix
diag = np.array([1 / k + (vol * x / h) ** 2 + rfr for x in s_seq[1:Jsize]])
under = np.array([(rfr - div) * x / 2 / h - 1 / 2 * (vol * x / h) ** 2 for x in s_seq[1:Jsize]])
over = np.array([-(rfr - div) * x / 2 / h - 1 / 2 * (vol * x / h) ** 2 for x in s_seq[1:Jsize]])
diag[0] = 2 * under[0] + diag[0]
over[0] = - under[0] + over[0]
diag[-1] = diag[-1] + 2 * over[-1]
under[-1] = under[-1] - over[-1]
# solve tridiagonal matrix
known = u[n, 1: Jsize] / k
unknown = thomas(under, diag, over, known)
u[n + 1, 1:Jsize] = unknown
# set boundary condition
u[n + 1, 0] = 2 * u[n + 1, 1] - u[n + 1, 2]
u[n + 1, -1] = 2 * u[n + 1, -2] - u[n + 1, -3]
return u, s_seq, t_seq
def thomas(a, b, c, d):
# 생략 (지난 글들 참고)
def Calculate_DigitalOption():
s0 = 100
strike = 100
upCoupon = 3
downCoupon = 1
maturity = 1
rfr = 0.02
vol = 0.2
div = 0.01
do_value_closedform = DigitalOption_ClosedForm(s0, strike, upCoupon, downCoupon, maturity, rfr, vol, div)
do_value_fdm, stock, timestep = DigitalOption_FDM_Implicit(s0, strike, upCoupon, downCoupon, maturity, rfr, vol,
div)
print('Digital Option Value by ClosedForm : {:.3f}'.format(do_value_closedform))
print('Digital Option Value by FDM : {:.3f}'.format(np.interp(s0, stock, do_value_fdm[-1, :])))
if __name__ == '__main__':
Calculate_DigitalOption()콜옵션, UOC의 가격 산출 코드와 완전히 유사하므로 아주 간략하게만 살펴보겠습니다.
# initial_condition
u[0, :] = np.array([upCoupon if s >= strike else downCoupon for s in s_seq])○ 거의 이 부분만 변경했습니다. 디지털 옵션의 만기 페이오프입니다.
print('Digital Option Value by FDM : {:.3f}'.format(np.interp(s0, stock, do_value_fdm[-1, :])))○ 선형 보간 함수를 써서 stock 배열에 매치된 함숫값 do_value_fdm[-1,:]에서 s0를 보간하여 찾아냈습니다. 선형 보간에 대한 간략한 설명은 여기에서 다루었으니 참고하시면 됩니다.
결과를 살펴보겠습니다.
Digital Option Value by ClosedForm : 1.921
Digital Option Value by FDM : 1.931Closed form의 결과와 아주 비슷하다는 것을 알 수 있습니다.
참고로 code내의 격자판 u를 모두 그려보겠습니다. 시점과 기초자산 그리고 함숫값을 축으로 하는 3차원 그래프이죠.
위 코드의
def Calculate_DigitalOption():이 함수의 끝에 다음의 코드를 추가하여 봅시다.
def Calculate_DigitalOption():
#생략
tt, ss = np.meshgrid(timestep, stock) #timestep과 stock 배열을 meshgrid로 만듬
print(ss.shape)
print(tt.shape)
print(do_value_fdm.shape) #ss, tt와 함수값의 shape이 동일한지를 확인하는 것
# do_value_fdm은 tranpose를 취해줘야 size가 맞음
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d') # 3D로 그릴것이라 선언함
ax.plot_surface(tt, ss, do_value_fdm.transpose(), alpha=0.5, color='blue')
# ax.view_init(0,0)
plt.show()갑자기 code에 모르는 문법이 많이 나왔지만, 3차원 그래프를 그려보는 것이 목적이므로 일단 설명은 생략하겠습니다.
결과를 보실까요.
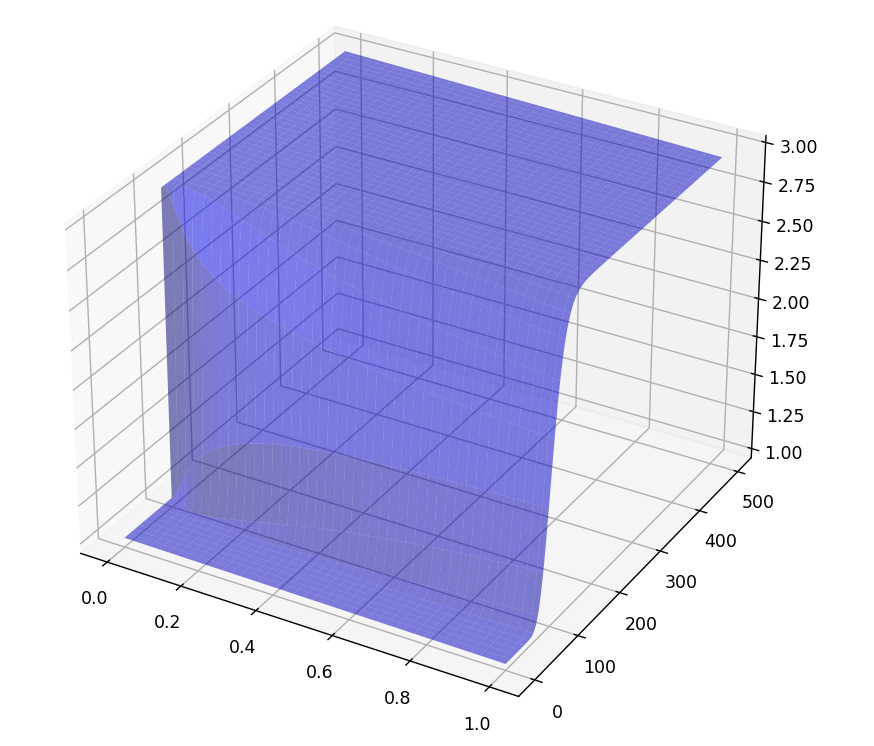
○ 훌륭한 3차원 그래프가 탄생했습니다.
○ 왼쪽의 끝단은 디지털 옵션의 만기 페이오프이고, 오른쪽 끝단은 디지털 옵션의 현재가치입니다. 노파심에 하는 말이지만 시간축의 값이 0일 때 만기 페이오프가 찍히는 이유는 뭘까요? 바로 경과시점이 아닌 잔존만기로 돌려 FDM을 풀었기 때문이죠. 현재 가격은 시간축의 값이 1일 때(즉 잔존만기가 1일 때)이고요.
(1001, 251)
(1001, 251)
(251, 1001)○ 밑에는 tt, ss와 함숫값의 shape을 출력해본 것입니다. FDM 결과인 do_value_fdm을 transpose 취해야 규격이 맞음을 알 수 있습니다.
다음 글에서는 디지털 옵션 가격을 구하는 마지막 방법, 바로 Binomial Tree를 이용하여 구해보겠습니다.
'금융공학' 카테고리의 다른 글
| 상관관계를 보이는 두 자산의 움직임 모델 (0) | 2022.09.30 |
|---|---|
| 디지털 옵션 #5. 디지털 옵션 가격, Binomial Tree (0) | 2022.09.02 |
| 디지털 옵션 #3. 디지털 옵션 가격, MonteCarlo Simulation (0) | 2022.09.01 |
| 디지털 옵션 #2. 디지털 옵션 Closed form 및 그래프 (0) | 2022.08.31 |
| 디지털 옵션 #1. 디지털 옵션이란? 수학공식은? (0) | 2022.08.30 |



댓글