지난 글
2022.08.19 - [금융공학] - 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM
옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM
저번 글 2022.08.18 - [금융공학] - 옵션 #3. 옵션 프리미엄 구하기(FDM) 옵션 #3. 옵션 프리미엄 구하기(FDM) 지난 글 2022.08.17 - [금융공학] - 옵션 #2. 옵션 프리미엄 구하기(Closed form) 옵션 #2. 옵션 프..
sine-qua-none.tistory.com
에서는 명시적 FDM의 방법을 사용하여 콜옵션 프리미엄 구하는 코드를 구형해 보았습니다. 지난 글 말미에서 명시적 FDM은 시간축과 주가 축의 격자를 어떻게 세팅하느냐에 따라 수렴이 깨져 원하는 결과를 얻지 못하는 한계가 있다고 설명을 했습니다. 그럼 함축적 FDM은 어떨까요?
함축적 FDM 복습
○ 잔존만기 grid를 0=τ0<τ1<⋯<τN=T 로 균등 분할하고, 격자의 간격을 k 라 합니다.
○ 기초자산 grid는 Smin=S0<⋯<SJ=Smax로 균등 분할하고, 격자 간격을 h라 합니다.
○ U(τn,Sj)를 unj으로 쓰면,
αjun+1j−1+βjun+1j+γjun+1j+1=unjk
이고 계수들은
αj=(r−q)Sj2h−σ2S2j2h2 , βj=1k+σ2S2jh2+r , γj=−(r−q)Sj2h−σ2S2j2h2
을 만족합니다.
○ 초기 조건은 u0j=max
○ 경계조건은 u_0^n - 2 u_1^n + u_2^n =0 ~~,~~ u_{J-2}^n - 2u_{J-1}^n +u_{J}^n =0
관계식(*)을 모든 j에 대해 그러모아 행렬 방정식으로 표현하면,
\pmatrix { 2\alpha_1+\beta_1 & -\alpha_1+\gamma_1 & 0 &\cdots & 0\\ \alpha_2 & \beta_2 & \gamma_2 &\cdots & 0 \\ 0 & \alpha_3 & \beta_3 & \cdots &0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots &\alpha_{J-2} &\beta_{J-2} &\gamma_{J-2}\\ 0 & 0 & \cdots &\alpha_{J-1}-\gamma_{J-1} & \beta_{J-1}+2\gamma_{J-1} } \cdot \pmatrix { u_1^{n+1} \\ u_2^{n+1} \\ \vdots\\ u_{J-2}^{n+1}\\ u_{J-1}^{n+1} } = \frac1k \pmatrix { u_1^{n} \\ u_2^{n} \\ \vdots\\ u_{J-2}^{n}\\ u_{J-1}^{n} }
입니다. 위 행렬 방정식에 등장하는 행렬을 순서대로 \mathbf{A}, \mathbf{u}^{n+1}, \mathbf{u}^n이라 하면
\mathbf{A} \cdot \mathbf{u}^{n+1} = \mathbf{u}^n \tag{1}
으로 쓸 수 있습니다. 보시다시피 \mathbf{A}는 3중 대각행렬(3중 대각행렬의 풀이)입니다.
따라서 \mathbf{u}^n을 알면 식(1)을 풀어 \mathbf{u}^{n+1}을 구할 수 있습니다. 즉 초기 조건 때문에 이미 알려진 \mathbf{u}^0에서 출발하여
\mathbf{u}^0 \rightarrow \mathbf{u}^1 \rightarrow \cdots \rightarrow \mathbf{u}^N
이런 식으로 풀어나가는 거죠. 식(1)을 푸는 방법은 두 가지가 있습니다.
1) \mathbf{u}^{n+1} = \mathbf{A}^{-1} \mathbf{u}^n 을 이용하여 계산
2) Thomas Algorithm을 이용함(3중 대각행렬의 풀이 참고)
그런데 3중 대각행렬의 풀이를 보시면, 역행렬에 의한 풀이는 계산 시간상 효율적이지 않죠. 따라서 함축적 FDM을 풀 때는 Thomas Algorithm을 사용합니다.
이제 프로그램을 구현해 볼까요?
Python Code
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
N = norm.cdf
def CallOptionBS(S, K, T, r, q, sigma):
if T == 0:
return np.max(S - K, 0)
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
return S * np.exp(-q * T) * N(d1) - K * np.exp(-r * T) * N(d2)
def Solve_BSEquation_1D_implicit():
# set parameters
s0, strike, rfr, mat, sigma, div = 100, 100, 0.02, 1, 0.3, 0.01
Nsize, Jsize = 100, 50
# s variable setting
s_min, s_max = 0, 5 * s0
s_seq = np.linspace(s_min, s_max, Jsize + 1)
h = s_seq[1] - s_seq[0]
# time variable setting
t_min, t_max = 0, mat
t_seq = np.linspace(t_min, t_max, Nsize)
k = t_seq[1] - t_seq[0]
print('criterion is {}'.format(k / (h ** 2)))
# solution grid u setting
u = np.empty((Nsize + 1, Jsize + 1))
# initial_condition
u[0, :] = np.array([max(s - strike, 0) for s in s_seq])
# recursive formula
for n in range(Nsize):
# make tridiagonal matrix
diag = np.array([1 / k + (sigma * x / h) ** 2 + rfr for x in s_seq[1:Jsize]])
under = np.array([(rfr - div) * x / 2 / h - 1 / 2 * (sigma * x / h) ** 2 for x in s_seq[1:Jsize]])
over = np.array([-(rfr - div) * x / 2 / h - 1 / 2 * (sigma * x / h) ** 2 for x in s_seq[1:Jsize]])
diag[0] = 2 * under[0] + diag[0]
over[0] = -1 * under[0] + over[0]
diag[-1] = diag[-1] + 2 * over[-1]
under[-1] = under[-1] - over[-1]
# solve tridiagonal matrix
known = u[n, 1: Jsize] / k
unknown = thomas(under, diag, over, known)
u[n + 1, 1:Jsize] = unknown
# set boundary condition
u[n + 1, 0] = 2 * u[n + 1, 1] - u[n + 1, 2]
u[n + 1, -1] = 2 * u[n + 1, -2] - u[n + 1, -3]
exact_value = np.array([CallOptionBS(s, strike, mat, rfr, 0, sigma) for s in s_seq[1:]])
# 편의상 배당률을 0으로 하드코딩함
fdm_value = np.array(u[-1, 1:])
bs = CallOptionBS(s0, strike, mat, rfr, div, sigma)
print('call price is {:.3f}'.format(bs))
jth = np.where(s_seq == s0)[0][0]
print('FDM call price is {:.3f}'.format(u[-1, jth]))
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(s_seq[1:], exact_value, label='exact value')
plt.plot(s_seq[1:], fdm_value, label='fdm value')
plt.title('Exact vs FDM')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(s_seq[1:], fdm_value - exact_value, label='value difference(FDM-Exact)')
plt.legend()
plt.show()
def thomas(a, b, c, d):
""" A is the tridiagnonal coefficient matrix and d is the RHS matrix"""
"""
a is lower diagonal a2,a3,..,a_N, meaning
b is diagonal b1,b2,b3,..,b_N meaning
c is upper diagonal c1,c2,c3,.. c_{N-1} meaning
"""
N = len(a)
cp = np.zeros(N, dtype='float64') # store tranformed c or c'
dp = np.zeros(N, dtype='float64') # store transformed d or d'
X = np.zeros(N, dtype='float64') # store unknown coefficients
# Perform Forward Sweep
# Equation 1 indexed as 0 in python
cp[0] = c[0] / b[0]
dp[0] = d[0] / b[0]
# Equation 2, ..., N (indexed 1 - N-1 in Python)
for i in np.arange(1, (N), 1):
dnum = b[i] - a[i] * cp[i - 1]
cp[i] = c[i] / dnum
dp[i] = (d[i] - a[i] * dp[i - 1]) / dnum
# Perform Back Substitution
X[(N - 1)] = dp[N - 1] # Obtain last xn
for i in np.arange((N - 2), -1, -1): # use x[i+1] to obtain x[i]
X[i] = (dp[i]) - (cp[i]) * (X[i + 1])
return (X)
if __name__ == '__main__':
Solve_BSEquation_1D_implicit()
전체적인 코드는 2022.08.19 - [금융공학] - 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM에서 다루었던 코드와 유사합니다. 따로 설명이 필요한 부분은 위 코드에 주석으로 적었습니다. 결과를 볼까요? 편의상 배당률은 0으로 하드코딩하였습니다.
criterion is 0.00010101010101010102
call price is 12.245
FDM call price is 12.712어떻습니까? closed form으로 구한 값과 아주 근사합니다. 그래프를 보겠습니다.
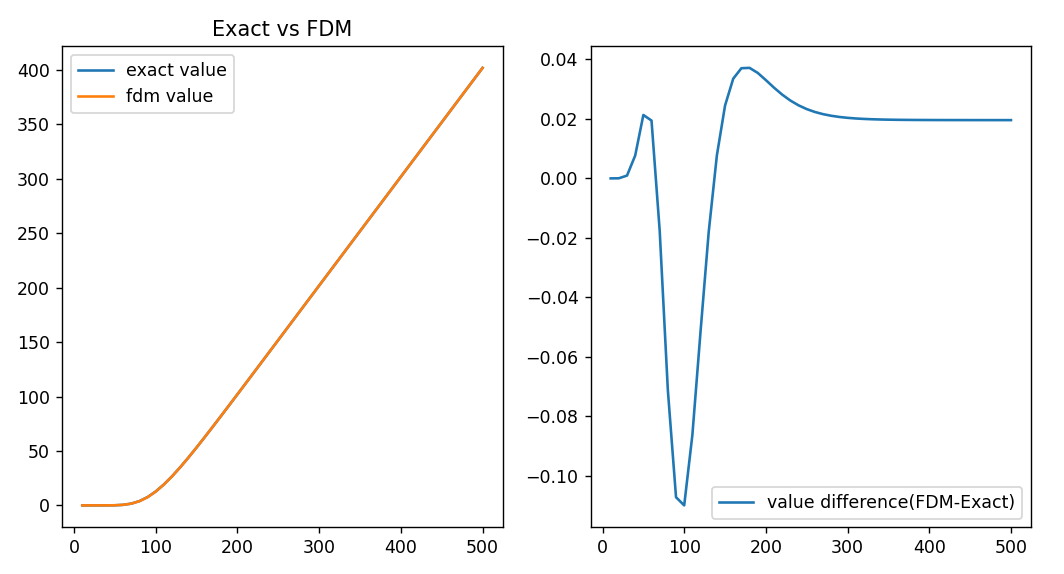
왼쪽 그래프는 closed form과 FDM으로 각각 얻는 그래프를 중첩한 결과입니다. 아주 훌륭하죠. 오른쪽 그래프는 FDM과 실제 값의 차이입니다. 오차가 0.05 도 안 날 정도입니다.
더 강조하고 싶은 건 바로 이 부분입니다.
Nsize, Jsize = 100, 50이 격자에서 명시적 FDM 방법은 값이 이상하게 나왔었죠. 2022.08.19 - [금융공학] - 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM의 결과 부분을 참고해 보세요.
함축적 방법은 다소 풀이과정이 복잡해 보여도 Thomas Algorithm을 알고 있으면 쉽게 해결되고, 무엇보다 어떤 격자를 가져다 놔도 값이 잘 나온다는 것이 장점입니다. 물론 격자를 성기게 자르면 값의 정확도가 조금은 떨어지겠죠. 일례로
Nsize, Jsize = 10, 10으로 성기 grid를 선택한다면 결과는 아래와 같습니다. 그렇다 하더라도 명시적 방법보다는 마음의 안정을 얻는 결과입니다.
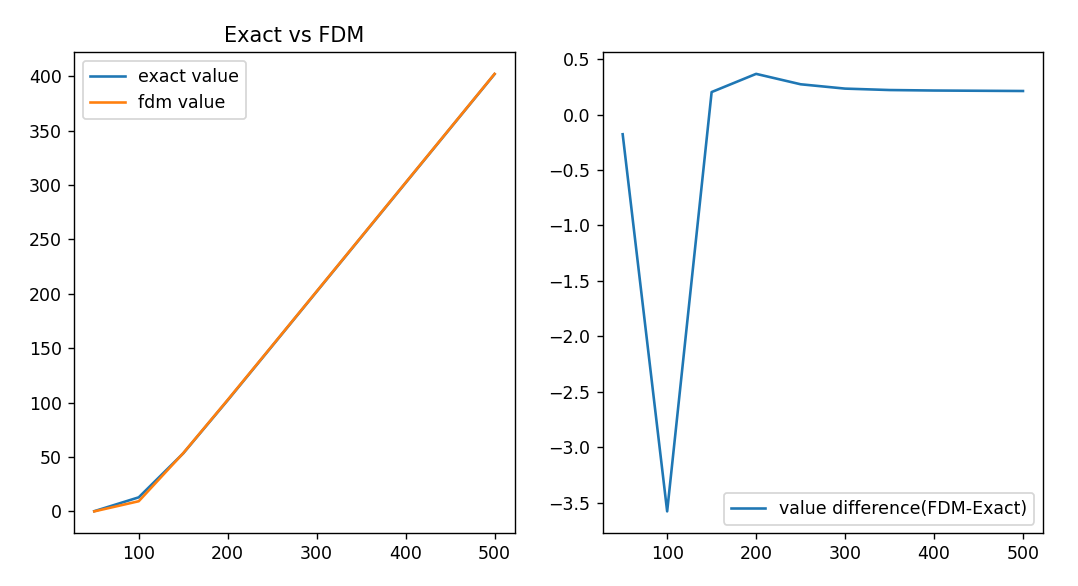
지금까지 2편의 글에 걸쳐 FDM을 이용한 콜옵션의 프리미엄 계산 과정을 살펴봤습니다.
이제 MonteCarlo Simulation 방법을 알아볼 차례입니다. 다음 글에서 계속됩니다.
'금융공학' 카테고리의 다른 글
| 옵션 #7. 옵션 프리미엄 구하기 실습: Binomial Tree (0) | 2022.08.22 |
|---|---|
| 옵션 #6. 옵션 프리미엄 구하기 실습: MonteCarlo Simulation (0) | 2022.08.21 |
| 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM (0) | 2022.08.19 |
| 옵션 #3. 옵션 프리미엄 구하기(FDM) (1) | 2022.08.18 |
| 옵션 #2. 옵션 프리미엄 구하기(Closed form) (0) | 2022.08.17 |



댓글