이번 글은
2022.08.19 - [금융공학] - 옵션 #5. 옵션 프리미엄 구하기 실습: 함축적 FDM
옵션 #5. 옵션 프리미엄 구하기 실습: 함축적 FDM
지난 글 2022.08.19 - [금융공학] - 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM 저번 글 2022.08.18 - [금융공학] - 옵션 #3. 옵션 프리미엄 구하기(FDM)..
sine-qua-none.tistory.com
에 이어서, 옵션 프리미엄을 구하는 다른 방법에 대해서 알아보는 내용입니다.
저번 글에서는 옵션 프리미엄을 명시적 FDM, 함축적 FDM 두 방법으로 해결하는 방법을 알아보았는데요. 이번에 알아볼 내용은
파생상품 가격 결정의 끝판왕: MonteCarlo Simulation(MC)
의 방법으로 가격을 구해보겠습니다. 우선 MonteCarlo Simulation을 복습해 볼까요?
MonteCarlo Simulation 복습
시뮬레이션 방법에 대해서는
2022.08.05 - [금융공학] - Black Scholes Equation의 풀이: 확률프로세스를 이용하자.
Black Scholes Equation의 풀이: 확률프로세스를 이용하자.
이번 글은 2022.08.04 - [금융공학] - Black Scholes Equation의 풀이 Black Scholes Equation의 풀이 이번 글은 2022.08.03 - [금융공학] - Black Scholes Equation과 Heat Equation의 관계 Black Scholes Equati..
sine-qua-none.tistory.com
에서 다뤘습니다. 실제로 시뮬레이션 방법으로 델타원 상품의 가격까지 구해봤드랬죠(2022.08.08 - [금융공학] - Black Scholes Equation의 풀이: 시뮬레이션을 참고하세요)
시뮬레이션 방법을 간단히 요약하면 이렇습니다.
Feynman-Kac Formula
편미분 방정식
ft(t,St)+(r−q)StfS(t,St)+12σ2S2tfSS(t,St)−rf(t,St)=0
의 해는
f(t,St)=e−r(T−t)EQ(f(T,ST)|Ft)
이다. 여기서 St는
dSt/St=(r−q)dt+σdWQt의 dynamics를 따른다.
특히 현재 시점 t=0에서는
f(0,S0)=e−rTEQ(f(T,ST))
이다.
온갖 확률 프로세스 이론을 도입하여 위의 결론을 얻었었는데, 얻은 결과가 어찌 보면 아주 자명해 보이죠? 아래의 방법대로 구하면 되는 것입니다.
- 만기 때 주가 ST가 어떻게 끝날지는 모르겠지만, 이것에 따라 만기 payoff F(T,ST)가 결정될 것이고
- F(T,ST) 들의 기댓값이 바로 파생상품의 미래가치가 된다.
- 따라서 이것을 현재가치로 할인해주면, 즉 e−rT를 곱하면
- 파생상품의 현재가치가 나온다.
본격적으로 콜옵션의 가격을 구해보도록 하겠습니다.
콜옵션 가격을 MC로 구하기
만기가 T, 행사가가 K인 콜옵션의 만기 payoff는
max
이라 주어집니다. 여기서 S_T는 기초자산의 T 시점에서의 가격이고, 기초자산 프로세스는 GBM
\textstyle{\frac{dS_t}{S_t} } = (r-q) dt + \sigma dW_t
를 따른다고 해보죠.
콜옵션의 시점 t, 기초자산의 가격이 S_t일 때 콜옵션 가격을 c(t,S_t)라 하면 식 (*)에 의해
c(t,S_t) = e^{-r(T-t)} \mathbb{E}^{\mathbb{Q}} ( \max(S_T-K,0) |\mathcal{F_t} )
입니다. 기초자산의 현재가를 S_0라 하면
c(0,S_0) = e^{-rT}\mathbb{E} ( \max(S_T-K,0) )
입니다.
이제 이것을 MC로 구해보죠. 구하는 과정은
2022.08.08 - [금융공학] - Black Scholes Equation의 풀이: 시뮬레이션에 있는 python code와 비슷합니다.
Python Code
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
N = norm.cdf
def CallOptionBS(S, K, T, r, q, sigma):
if T == 0:
return np.max(S - K, 0)
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
return S * np.exp(-q * T) * N(d1) - K * np.exp(-r * T) * N(d2)
def call_option_by_MC():
s0 = 100
vol = 0.3
r = 0.02
d = 0.01
maturity = 1
strike = 100
nSimulation = 1000000
drift = (r - d - 0.5 * vol ** 2) * maturity
volsqrtmat = vol * np.sqrt(maturity)
rn = np.random.normal(size=nSimulation)
s_maturity = s0 * np.exp(drift + volsqrtmat * rn)
payoff = np.array([np.max([0, s_mat - strike]) for s_mat in s_maturity])
s_cum_mean = np.cumsum(payoff) / np.arange(1, nSimulation + 1) * np.exp(-r * maturity)
simulation_result = np.mean(payoff) * np.exp(-r * maturity)
exact_solution = CallOptionBS(s0, strike, maturity, r, d, vol)
print('result of simulation :{:.3f}'.format(simulation_result))
print('result of exact solution: {:.3f}'.format(exact_solution))
print('result of s_cum_mean: {:.3f}'.format(s_cum_mean[-1]))
plt.figure(figsize=(10, 10))
plt.suptitle('call option price by MC')
sim_list = [100, 1000, 10000, 100000]
for i in range(len(sim_list)):
plt.subplot(2, 2, i + 1)
plt.plot(s_cum_mean[:sim_list[i]], label='{} iteration'.format(sim_list[i]))
plt.hlines(exact_solution, 0, sim_list[i], color='r')
plt.legend()
plt.show()
# plt.plot(s_cum_mean, color='c')
# plt.hlines(exact_solution, 0, nSimulation - 1, color='r')
# plt.show()
if __name__ == '__main__':
call_option_by_MC()
코드를 간략히 살펴보겠습니다.
def CallOptionBS(S, K, T, r, q, sigma):
# closed form과 비교하기 위해 사용자 정의한 함수입니다.
def call_option_by_MC():
s0 = 100 # 기초자산의 현재가
vol = 0.3 # 기초자산의 변동성
r = 0.02 # 무위험이자율
d = 0.01 # 기초자산의 연속배당률
maturity = 1 # 콜옵션의 만기
strike = 100 # 콜옵션의 행사가
nSimulation = 1000000 # 총 nSimulation 개의 기초자산 만기가격을 생성할 예정
drift = (r - d - 0.5 * vol ** 2) * maturity # 기초자산의 drift 항
volsqrtmat = vol * np.sqrt(maturity) # 기초자산의 diffusion 항
rn = np.random.normal(size=nSimulation) # nSimulation 개의 표준정규분포 난수를 발생시켜
s_maturity = s0 * np.exp(drift + volsqrtmat * rn) # nSimulation개의 만기 종가를 생성한다.○ S_T = S_0 \exp((r-d-{\textstyle \frac12}\sigma^2)T + \sigma \sqrt{T} z) 라는 식을 이용하여 S_T를 만드는 것입니다.
payoff = np.array([np.max([0, s_mat - strike]) for s_mat in s_maturity])
# 만기종가 각각에 대해 콜옵션 payoff max(S_T-K,0)를 계산하여 payoff라는 배열 만듬
s_cum_mean = np.cumsum(payoff) / np.arange(1, nSimulation + 1) * np.exp(-r * maturity)
# 아래 설명○ 전체 시뮬레이션 횟수를 N회라 했을 때, 총 N개의 payoff X_1, X_2, \cdots, X_N이 생성될 것입니다. 이때,
a_n = (X_1+\cdots+X_n)/n이라 두면, a_n 은 n번째 시뮬레이션까지의 기댓값이 되겠죠. 따라서 이 값을 구하여 시뮬레이션 횟수가 증가할 때 평균값이 어디로 수렴하는지를 볼 수 있습니다.
○ numpy.cumsum(payoff)는 payoff 배열을 첫 항부터 누적하여 합한 것을 다시 배열로 만든 것입니다. 이를 {\rm{array}}([1,2,\cdots,N])으로 시뮬레이션 횟수가 증가하며 생기는 평균(기댓값)들을 모으는 것입니다.
결과를 보시죠.
result of simulation :12.237
result of exact solution: 12.245
result of s_cum_mean: 12.237MC로 구한 값은 12.237이고, Black Sholes formula 즉 closed form으로 구한 값은 12.245로서 MC 방법도 파생상품의 해를 구하는 훌륭한 방법이라는 것을 알았습니다. 시뮬레이션 별 횟수에 따른 옵션 가격의 수렴도를 볼까요?
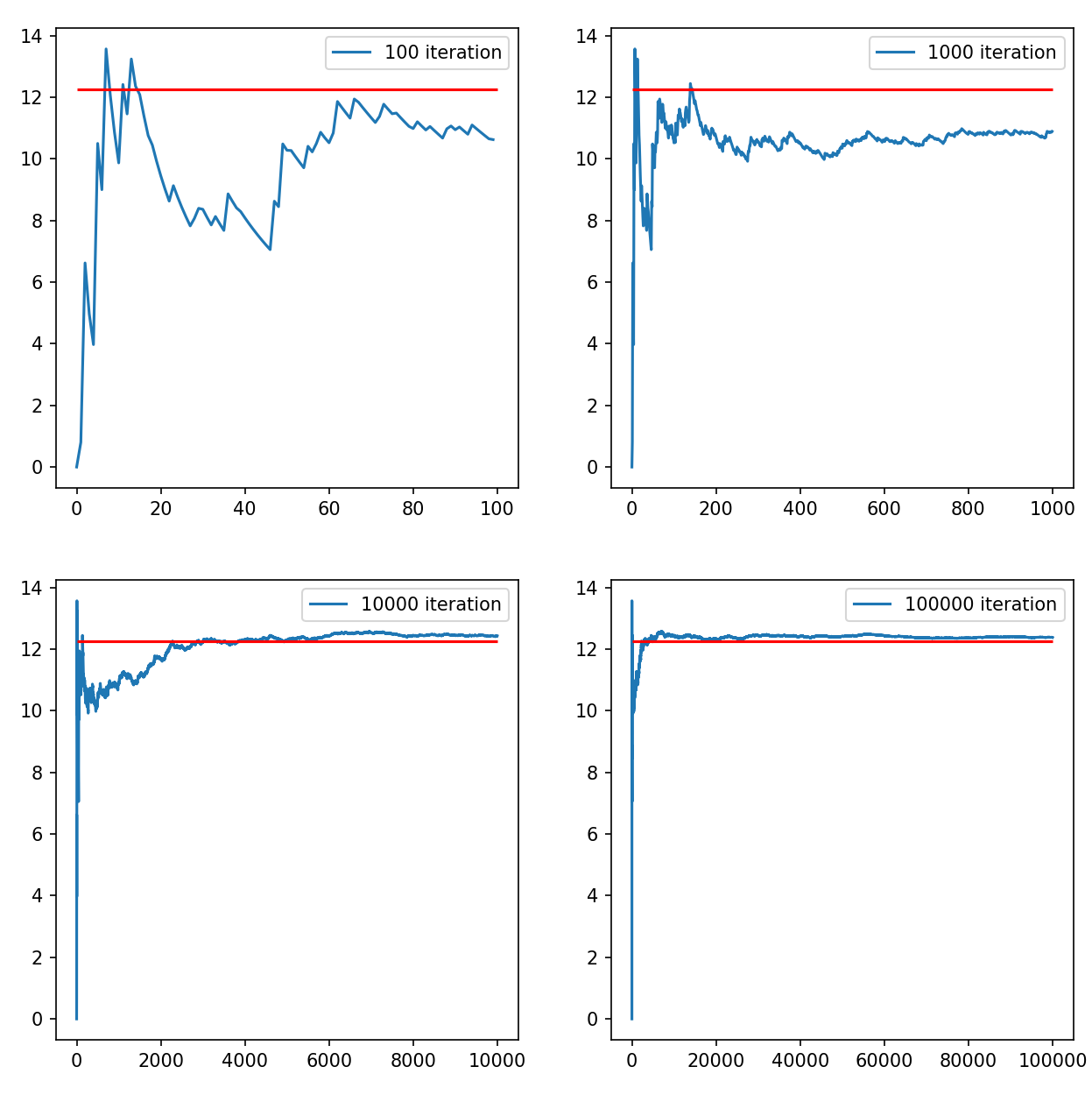
빨간색 선이 exact soluation인 12.245입니다. 시뮬레이션 100회나 1000회는 exact value랑 아직 많이 이격 되어 있는 모습을 볼 수 있습니다. 시뮬레이션 횟수가 증가할수록 빨간색 선에 수렴하는 모습을 보이죠? MC 시뮬레이션 횟수가 많으면 많을수록 정확한 값에 수렴하게 됩니다. 하지만 계산 시간이 많이 걸리겠죠, 따라서 MC를 사욯할 때는 서로 trade off관계가 있는
- 계산의 정확성
- 계산 시간의 효율성
을 잘 따져서 시뮬레이션 횟수를 결정하는 것이 좋습니다.
다음 시간에는 옵션 가격을 구하는 또 다른 방법에 대해서 알아보겠습니다.
'금융공학' 카테고리의 다른 글
| 옵션 #8. 옵션 프리미엄 구하기 실습: Binomial Tree(with VBA) (0) | 2022.08.22 |
|---|---|
| 옵션 #7. 옵션 프리미엄 구하기 실습: Binomial Tree (0) | 2022.08.22 |
| 옵션 #5. 옵션 프리미엄 구하기 실습: 함축적 FDM (0) | 2022.08.19 |
| 옵션 #4. 옵션 프리미엄 구하기 실습: 명시적 FDM (0) | 2022.08.19 |
| 옵션 #3. 옵션 프리미엄 구하기(FDM) (1) | 2022.08.18 |




댓글