Black Scholes Equation의 풀이: 시뮬레이션

이번 글은

2022.08.05 - [금융공학] - Black Scholes Equation의 풀이: 델타원 상품

Black Scholes Equation의 풀이: 델타원 상품

에서 이어집니다.

 

만기 때 pyaoff를 기초자산 그 자체로 주는, 즉 만기 시점 $T$에 

$$f(T,S_T) =S_T$$

를 주는 파생상품의 현재 시점  $t=0$, 기초자산의 현재가 $S_0$의 파생상품의 가격 $f(0,S_0)$는

$$ \begin{align}f(0,S_0 ) &= e^{-rT} \mathbb{E}^{\mathbb{Q}} ( f(T,S_T))\\&=S_0 e^{-dT}\end{align}$$

이라는 것을 보였습니다.

 

마지막 등호는 기댓값을 수식으로 잘 정리해서 얻은 결과였지요. 하지만 이렇게 수식으로 exact solution을 얻는 일은 참으로 드뭅니다. 아주 좋은 형태의 페이오프에 대해서만 풀리게 되죠.

 

만일 수식으로 정리될 수 있는 형태가 아니라면,

 

$$ f(0,S_0) =  e^{-rT} \mathbb{E}^{\mathbb{Q}} ( f(T,S_T)) $$

를 다른 방법으로 구할 수밖에 없습니다.

 

자, 이제 델타원 상품 즉, $f(T,S_T)=S_T$인 상품의 현재가치를 한 번 구해보겠습니다

 

 

시뮬레이션

우리의 목표는

$$ e^{-rT} \mathbb{E}^{\mathbb{Q}}(S_T) $$

의 가격을 구하는 것입니다. 절차는 다음과 같습니다.

 

1. $S_T$  표본(sample) 여러 개 생성하기

$$ S_T = S_0 \exp\left( \left(r-d-\frac12\sigma^2\right)T+\sigma W_T \right)$$

임은 익히 알고 있습니다. 또한

$$W_T \sim \mathcal{N}(0,\sqrt{T}^2)$$

이므로, 만일 표준정규분포를 따르는 난수 $z$를 하나 뽑는다면

$$ S_T =  S_0 \exp\left( \left(r-d-\frac12\sigma^2\right)T+\sigma\sqrt{T} z \right) \tag{1}$$

로 $S_T$를 생성할 수 있죠.

 

따라서 표준 정규분포를 따르는 $N$개의 난수 $z_1, z_2, \cdots, z_N$를 생성하고 식(1)을 이용하여 각각에 대응하는 

$$ S_T^{(1)}, S_T^{(2)}, \cdots , S_T^{(N)}\tag{2}$$ 

을 생성합니다.

 

2. 표본 평균 구하기

식(2)의 표본들의 평균

$$\bar{S} = \frac{1}N \left(S_T^{(1)} +\cdots +S_T^{(N)} \right)$$

를 구하면, 큰 수의 법칙에 의해 표본 평균 $\bar{S}$는 모평균 즉,

$$ \mathbb{E}^{\mathbb{Q}}(S_T)$$

에 가까워집니다. $N$이 커질수록, 즉 샘플의 개수가 늘어날수록 훨씬 더 높은 정확도를 자랑하게 되죠. 즉 충분히 큰 $N$에 대해

 

$$ \mathbb{E}^{\mathbb{Q}}(S_T) \approx \frac{1}N \left(S_T^{(1)} +\cdots +S_T^{(N)} \right)\tag{3}$$

로 구할 수 있습니다.

 

참고로 큰 수의 법칙은 다음과 같습니다.

큰수의 법칙

표본집단의 크기가 커지면 그 표본 평균이 모평균에 가까워짐을 의미함. 수식적으로는 다음과 같습니다.
독립 항등 분포(i.i.d)인 $X_1, X_2, \cdots,  X_n$ 의 모평균이 $\mu$일 때, 임의의 $\epsilon>0$에 대해서
$$\lim_{n\rightarrow\infty}\mathbb{P}\left(\Big| \frac1n \sum_{i=1}^n X_i -\mu \Big| \right) =1 $$
가 성립합니다.

내려갈 팀은 내려간다 - 큰수의 법칙을 증명하며 시대를 풍미했던 야구 이론 DTD

 

3. 할인 팩터 곱하여 결과 산출

미래 시점 $T$의 페이오프를 현재 시점으로 할인해 오기 위해 

$$ e^{-rT}$$

를 구하여 식(3)에 곱하면 끝이 납니다. 정리하면

$$ f(0,S_0) = e^{-rT} \sum_{i=1}^N S_T^{(i)} $$

입니다.

 

 

코딩

python으로 위와 같은 내용을 코딩해 봅시다.

 

import numpy as np
import matplotlib.pyplot as plt


def test_BSEquation():
    s0 = 100
    vol = 0.3
    r = 0.02
    d = 0.01
    maturity = 1

    nSimulation = 1000
    drift = (r - d - 0.5 * vol ** 2) * maturity
    volsqrtmat = vol * np.sqrt(maturity)

    rn = np.random.normal(size=nSimulation)
    s_maturity = s0 * np.exp(drift + volsqrtmat * rn)
    
    s_cum_mean = np.cumsum(s_maturity) / np.arange(1, nSimulation + 1) * np.exp(-r * maturity)
    simulation_result = np.mean(s_maturity) * np.exp(-r * maturity)
    exact_solution = s0 * np.exp(-d * maturity)

    print('result of simulation :{:.3f}'.format(simulation_result))
    print('result of exact solution: {:.3f}'.format(exact_solution))
    print('result of s_cum_mean: {:.3f}'.format(s_cum_mean[-1]))
    plt.plot(s_cum_mean, color='c')
    plt.hlines(exact_solution, 0, nSimulation - 1, color='r')
    plt.show()


if __name__ == '__main__':
    test_BSEquation()

 

간단히 코드를 살펴보자면,

    nSimulation = 1000		#표본의 개수는 nSimulation개로 합니다.
    drift = (r - d - 0.5 * vol ** 2) # maturity	#S_T 계산을 위해 효율적으로 drift와
    volsqrtmat = vol * np.sqrt(maturity)	#diffusion 항을 따로 계산해 놓음	

    rn = np.random.normal(size=nSimulation)	# 표본의 개수만큼 정규분포 난수를 추출함

 

---

    s_cum_mean = np.cumsum(s_maturity) / np.arange(1, nSimulation + 1) * np.exp(-r * maturity)
    	# s_maturity 의 원소값을 누적으로 합한 것을 합해진 숫자만큼으로 나눈 값, 즉 표본 첫 i개의 평균
        # 을 의미. 여기에 할인팩터를 곱함
        
    simulation_result = np.mean(s_maturity) * np.exp(-r * maturity)
    	# 전체 표본의 평균에 할인팩터를 곱함
        
    exact_solution = s0 * np.exp(-d * maturity)
    	# exact solution : S0 e^{-dT}

 

 

 

결과

 

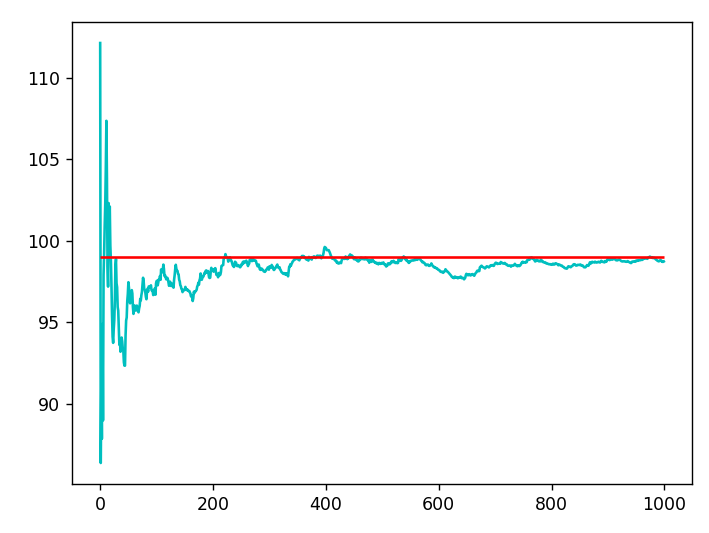
result of simulation :98.729
result of exact solution: 99.005
result of s_cum_mean: 98.729

를 얻습니다. cumsum을 사용하여 표본 개수가 증가할 때, 표본의 평균이 어떻게 변하는지를 구하여 나타낸 변화(청록색 곡선)가 빨간 선(exact solution)으로 계속 수렴해 가는 것을 볼 수 있죠.

 

위 코드에서는 효과를 잘 보기 위해 시뮬레이션 횟수를 1000개로 작게 잡았는데, 백만, 천만 등으로 표본의 개수를 늘리면 exact solution과 거의 비슷해집니다.

 

 

 

결론

아니 굳이 exact solution을 알고 있는데, 이런 계산을 왜 하냐 싶기도 하지만, exact solution을 구할 수 있는 경우가 거의 없기 때문이죠. 만기 payoff가 조금이라도 복잡하거나 하면 수식적으로 공식을 풀어내기가 불가능합니다. 이럴 때는 근사치라도 구해야 하는데, 그러기 위해서는 이 방법만큼 좋은 방법은 없습니다.

이렇게 샘플을 추출하여 표본 평균을 구해 값의 근사치를 구하는 방법을 시뮬레이션 또는

몬테카를로 시뮬레이션(MonteCarlo Simulation)

이라 합니다. 구하는 방법이 간단하므로 꼭 숙지해 놓으면 도움이 됩니다. 사실 몬테카를로 시뮬레이션은 이 블로그 여기저기에서 다룬 내용입니다. 예를 들어

• 2022.07.01 - [수학의 재미/시뮬레이션] - 순간의 선택으로 득템 하자. 몬티홀 문제
• 2022.06.30 - [수학의 재미/시뮬레이션] - e를 시뮬레이션으로 구하기
• 2022.06.09 - [수학의 재미/시뮬레이션] - 판별식을 시뮬레이션으로?

이런 글들이었죠. 위 방식과 철학이 똑같은 이야기들입니다. 관심 있으시면 한 번씩 보시기 바랍니다.