확률 통계 분야에 아주 유명한 문제가 있습니다. 몬티 홀 문제(Monty Hall problem)인데요.
사실 몬티 홀은 사람 이름입니다. 미국 퀴즈 프로그램의 진행자였던 Monty Hall의 이름이 붙게 된 문제입니다.

몬티홀 문제는 1990년 [퍼레이드]라는 잡지에 소개되면서 확률분야의 유명한 문제로 알려지게 되는데, 그 잡지에 실린 원문을 그대로 써보면 다음과 같습니다(나무위키 참조)
Suppose you’re on a game show, and you’re given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say #1, and the host, who knows what’s behind the doors, opens another door, say #3, which has a goat. He says to you, "Do you want to pick door #2?" Is it to your advantage to switch your choice of doors?
당신이 한 게임 쇼에 참여하여 세 문들 중 하나를 고를 기회를 가졌다고 생각해봐라. 한 문 뒤에는 자동차가 있으며, 다른 두 문 뒤에는 염소가 있다. 당신은 1번 문을 고르고, 문 뒤에 무엇이 있는지 아는 사회자는 염소가 있는 3번 문을 연다. 그는 당신에게 "2번 문을 고르고 싶습니까?"라고 묻는다. 당신의 선택을 바꾸는 것은 이득이 되는가?
결론부터 말하면 선택을 바꾸는 게 이득이 됩니다. 자동차를 얻을 확률이 높아지는 거죠.
간략히 살펴보면 이렇습니다.

그런데 Monty Hall 께서 참여자가 고르지 않은 문 중에, 자동차가 없는 방을 공개하죠. 즉 만일 참여자가 Room#1을 처음에 골랐다 하면 Monty Hall 께서는 3번 방을 폭파시키죠.

그런데 그림을 딱 보면,
- 참여자가 애시당초 자동차 방을 선택할 확률은 1/3
- 다른 두 방 중 하나에 자동차가 있을 확률은 2/3
입니다. 근데 Monty Hall 께서 2/3 확률을 가진 방 2개 중에 필요 없는 거 하나를 공개했죠? 따라서 위의 사실이 아래처럼 바뀝니다.
- 참여자가 애시당초 자동차 방을 선택할 확률 1/3
- 다른 한 방((왜냐면 한 방은 사회자가 열어버렸으므로)) 중 하나에 자동차가 있을 확률 2/3
따라서 참여자는 자신의 선택을 뒤집어서 자동차를 고를 확률을 높일 수 있다는 이야기죠.
더 자세한 사례는 Korea 위키피디아에 있습니다. 아래 그림을 살펴보면 이해가 쉬울 겁니다.
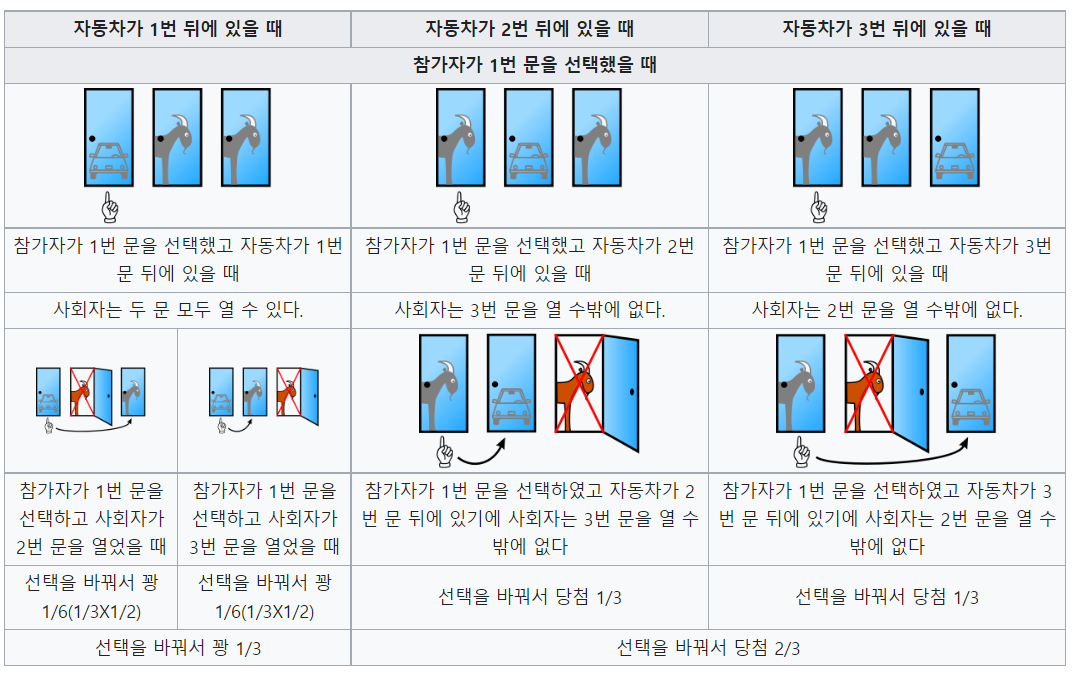
사실 이문제는 답이 명확함에도 불구하고 세계 유수의 학자들이나 머리 좀 쓴다 하는 브레인 고수들을 수십 년 동안 헷갈리게 만든 악명 높은 문제입니다. 가만 생각하면, 사회자가 문 하나 열어줬다고 해서 확률이 바뀌는 건가 싶은 거거든요.
이론적으로는 어쨋든 선택을 바꾸는 게 유리한데, 이게 맞는지 코드를 통해서 알아볼까요?
import matplotlib.pyplot as plt
import random
def Monty_Hall_Problem():
room = ['goat', 'car', 'goat']
switch_win_prob = []
myway_win_prob = []
nSimulation = 10
switch, myway = 0, 0
for i in range(nSimulation):
random.shuffle(room)
k = random.randint(0, 2)
if room[k] != 'car':
switch += 1
else:
myway += 1
switch_win_prob.append(switch / (i + 1))
myway_win_prob.append(myway / (i + 1))
plt.plot(switch_win_prob, c='c', label='switch win prob changes')
plt.plot(myway_win_prob, c='m', label='no action win prob changes')
plt.text(nSimulation / 2, switch_win_prob[-1] * 1.1, 'switch win \nprob:{:.2f}'.format(switch_win_prob[-1]))
plt.text(nSimulation / 2, myway_win_prob[-1] * 0.6, 'myway win \nprob:{:.2f}'.format(myway_win_prob[-1]))
plt.title('Simulation {} times'.format(nSimulation))
plt.show()
if __name__ == '__main__':
Monty_Hall_Problem()
code를 간략분석하면 다음과 같습니다.
room = ['goat', 'car', 'goat']
switch_win_prob = []
myway_win_prob = []
nSimulation = 10
switch, myway = 0, 0○ room 3원소 list를 정합니다.
○ switch_win_prob 는 선택을 변경해서 자동차를 얻을 확률, myway_win_prob는 선택을 고집하여 자동차를 얻을 확률을 시뮬레이션 횟수를 증가시키며 계산하여 저장하는 변수
○ 선택변경으로 자동차 득템 횟수와 선택 고집으로 자동차 득템횟수를 각각 switch, myway라 함
for i in range(nSimulation):
random.shuffle(room)
k = random.randint(0, 2)
if room[k] != 'car':
switch += 1
else:
myway += 1
switch_win_prob.append(switch / (i + 1))
myway_win_prob.append(myway / (i + 1))○ random.shuffle 함수로 방을 막 섞음. 방1,2,3에 랜덤 하게 자동차 및 염소 배치
○ 퀴즈 참여자가 방3개에 대응하는 index 하나를 고름. k=random.randint(0,2)
○ 만일 참여자가 고른 방이 애당초 자동차 방이 아니었다면 선택 변경함으로써 무조건 자동차 득템 -> switch 증가
○ 애시당초 자동차 방이었다면 괜히 변경하면 염소 득템, 따라서 안 바꿔야 자동차 득템
○ 누적된 횟수를 $i+1$로 나눠주면(파이썬은 i=0부터 시작하므로) 시뮬레이션 횟수당 확률이 나옴
결과를 보실까요?
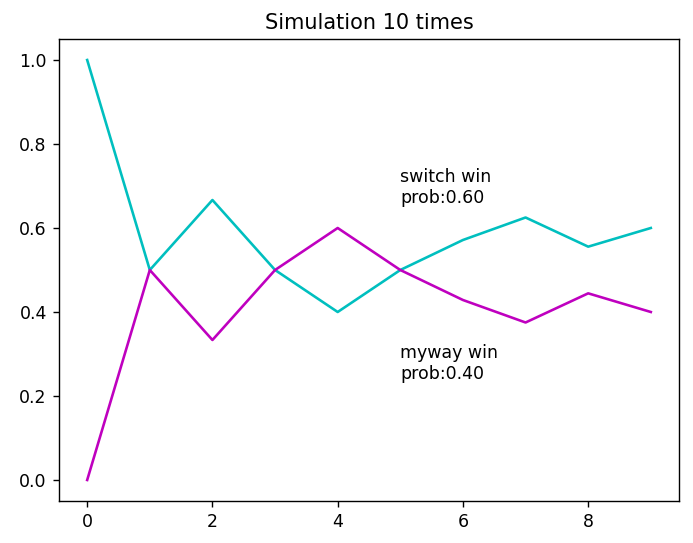
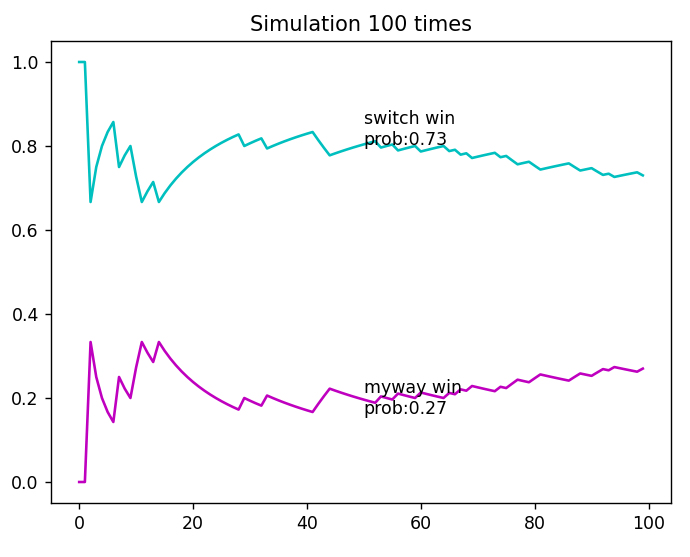
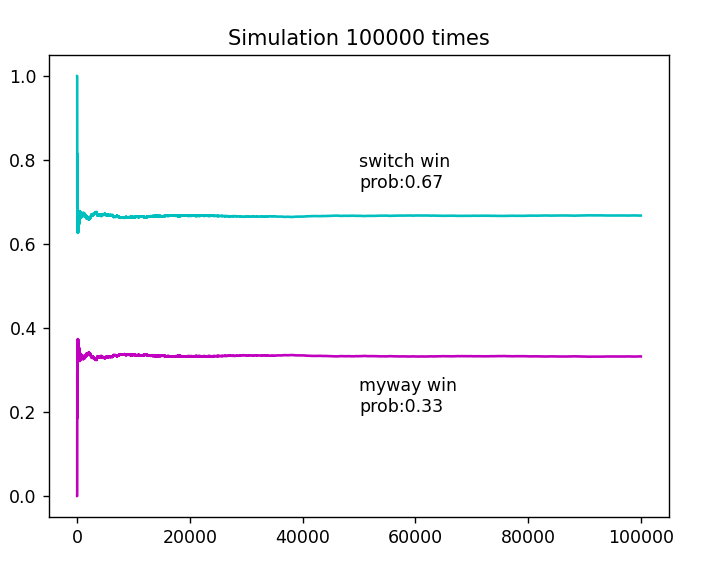
시뮬레이션 결과에서도 볼 수 있듯이, 선택을 바꿔서 성공할 확률이 $\frac23$, 실패할 확률이 $\frac13$이므로 참여자는 선택을 바꾸는 게 현명해 보입니다.
염소랑 차에 대한 자료를 찾다보니, 재밌는 사진이 있네요.

'수학의 재미 > 시뮬레이션' 카테고리의 다른 글
| e 를 시뮬레이션으로 구하기 (0) | 2022.06.30 |
|---|---|
| 판별식을 시뮬레이션으로? (0) | 2022.06.09 |


댓글