Binomial Tree #1: GBM을 단순하게!

GBM 모델은 다음과 같습니다.

무위험 이자율을 $r$, 연속배당률을 $q$라 하면

$$ dS_t/S_t= (r-q) dt + \sigma dW_t$$

 

어떤 시간 간격 $\Delta t$에 대해 시점 $t$와 시점 $t+\Delta$ 사이의 주가의 관계식은

$$S_{t+\Delta t}  = S_t \exp \left( \left(r-q-\frac12\sigma^2 \right) \Delta t + \sigma W_{\Delta t} \right) \tag{GBM}$$

 

$S_t$가 결정되어 있을 때, $S_{t+\Delta t}$를 결정하는 것은 다름아닌 $W_{\Delta t}$이죠. 이것은 정규분포 $\mathcal{N}(0,\sqrt{\Delta t}^2)$을 따르기 때문에 $S_{t+\Delta t}$가 나오는 건, 시쳇말로 무한개갰죠. 연속확률분포니까요.

 

 

Motivation

이것을 좀 더 간단화시켜, 기초자산 $S_t$가 일정 비율 오르고(up),  일정 비율 내리는(down) 모델을 생각해 봅시다. 

상승 비율을 $u$, 하락비율을 $d$라 하고,  $S$를 상승했을 때, $S\cdot u$, 하락했을 때, $S\cdot d$ 두 경우로 가정합니다. 그리고 상승확률을 $p$, 하락 확률을 $1-p$라 합시다. 표로 정리하면 이렇습니다.

현재 주가를 $S$라 할 때,

 

상태	up	down
변수	$S\cdot u$	$S\cdot d$
확률	$p$	$1-p$

 

 

 

우리의 목적은 위 그림의 상승, 하락비율 $u,d$와 확률 $p$값을 찾는 것입니다. 하지만 아무렇게나 찾으면 안 되겠죠. 

주가 $S$가 GBM 모델하에서 가지는 특징들을 유지할 수 있도록 만드는 것이 중요

합니다. 이제 분석을 해 볼까요? 

참고로, 위의 모델을 변수가 2개의 값을 가진다고 해서 이항 모델 영어로는 binomial model이라고 합니다.

 

 

이항 모델이 만족할 조건

이항 모델이 다음의 성질을 만족했으면 좋겠습니다.

 

1. 이항 모델은 최대한 간결하게!
2. $S_{t+\Delta t}$의 기댓값이  GBM 모델에서의 기댓값과 같으면 좋겠다.
3. $S_{t+\Delta t}$의 분산이 GBM 모델에서의 분산과 같으면 좋겠다. 

1. 이항 모델의 간결성

이항 모델이 간결해지는 걸 위해 주가가 올라갔다 내려왔을 때, 자기 자신이 되는 세팅을 해 봅시다. 즉,

$$ S= (Su)d= (Sd)u$$

를 원하므로 

$$ud=1\tag{1}$$

이라 합시다.

 

2,3. 평균과 분산의 일치

 

우선 1,2번을 위해, 식 (GBM)에서 $S_{t+\Delta t}$의 기댓값과 2차 모멘텀(분산을 의미)을 구하면 다음과 같습니다.

 

$$\mathbb{E}(S_{t+\Delta t} ) = \mathbb{E}\left[S_t \exp \left( \left(r-q-\frac12\sigma^2 \right) \Delta t + \sigma W_{\Delta t} \right)\right] = S_te^{(r-q)\Delta t}$$

 

$$\mathbb{E}(S_{t+\Delta t}^2  ) = \mathbb{E}\left[S_t^2 \exp \left( 2\left(r-q-\frac12\sigma^2 \right) \Delta t +2 \sigma W_{\Delta t} \right)\right] = S_t^2 e^{(2r-2q+\sigma^2)\Delta t}$$

 

그런데, 이항 모델하에서 위 두식의 좌변을 보면,  짧은 시간의 변화 $\Delta t$ 동안

$S_{t+\Delta t}$가 될 수 있는 값은 $S_t \cdot u , S_T\cdot d$ 두 가지이므로

 

$$
\begin{align}
pS_tu+(1-p)S_t d &=\mathbb{E}(S_{t+\Delta t} ) =S_t e^{(r-q)\Delta t}\\
p(S_tu)^2 + (1-p)(S_t d)^2 & =  \mathbb{E}(S_{t+\Delta t}^2 ) =S_t e^{(2r-2q+\sigma^2)\Delta t}
\end{align}
$$

입니다. 이것을 더 간단히 정리하면

$$
\begin{align}
pu+(1-p) d &= e^{(r-q)\Delta t}\tag{2}\\
pu^2 + (1-p)d^2 & = e^{(2r-2q+\sigma^2)\Delta t}\tag{3}
\end{align}
$$

 

식(2),(3)을 각각 정리하면

$$
\begin{align}
(u-d)p+ d &= e^{(r-q)\Delta t}\tag{4}\\
(u^2-d^2)p +d^2 & = e^{(2r-2q+\sigma^2)\Delta t}\tag{5}
\end{align}
$$

입니다.

 

이항 모델의 계산

우선 식 (4)에서 두 확률을 구할 수 있습니다.

up &down 확률
$$ \begin{align} p &= \frac{e^{(r-q)\Delta t}-d}{u-d}\\ 1-p &= \frac{u-e^{(r-q)\Delta t}}{u-d} \tag{PROB}\\ \end{align} $$

이제, $u,d$만 결정되면 되겠죠.

 

식(4) $\times (u-d) -$  식(5)을 하면

$$ 1= e^{(r-q)\Delta t} (u+d) - e^{(2r-2q+\sigma^2)\Delta t}$$

따라서

$$ u+d = e^{(r-q+\sigma^2 )\Delta t}  + e^{-(r-q)\Delta t}\tag{6}$$

을 만족합니다. 식(1)과 (6)을 종합하면

$u, d$ 값은?

$u, d$는 2차 방정식
$$ x^2 -\left( e^{(r-q+\sigma^2 )\Delta t}  + e^{-(r-q)\Delta t} \right)x +1 =0$$
의 두 근임. 그중 1보다 큰 값이 $u$, 작은 값이 $d$임

를 얻습니다.  그런데 식이 상당히 복잡합니다. 

$$ A= e^{(r-q+\sigma^2 )\Delta t}  + e^{-(r-q)\Delta t} $$ 라 하고 근의 공식을 쓰면

 

$$\begin{align}
u&= \frac{A+\sqrt{A^2-4}}2 \\
d&= \frac{A-\sqrt{A^2-4}}2 \tag{7}\\
\end{align}$$

 

입니다. 이 복잡한 식을 좀 깔끔하게 근사 시켜 볼까요?(어차피 정규분포를 이항으로 바꾼 과정 자체가 정확한 값이 아닌 근삿값을 허용한다는  뜻이므로 조금 더 깔끔하게 근사 시키는 것은 무리가 아니겠죠)

 

깔끔한 정리를 위하여 $e^x$의 테일러 전개를 이용합니다. 

$$ e^x = 1+x+\frac1{2!} x^2 + \frac1{3!}x^3 +\cdots $$

 

이제 $A$를 정리해 보면

 

$$\begin{align}
A&= e^{(r-q+\sigma^2 )\Delta t}  + e^{-(r-q)\Delta t}\\
 & = 1+(r-q+\sigma^2)\Delta t + 1-(r-q)\Delta t +\cdots \\
& = 2+ \sigma^2 \Delta t  + \Delta t^2(\cdots) 
\end{align}$$

 

$\Delta t^2$이 무시할 정도로 작다고 하면,  $A=2+\sigma^2 \Delta t$이고

$$ A^2 -4= 4\sigma^2 \Delta t + \sigma^4 \Delta t^2 \approx 4\sigma^2\Delta t$$

이므로 

$$ u, d\approx\frac12 (2+\sigma^2\Delta t \pm \sqrt{4\sigma^2 \Delta t})= 1\pm \sigma \sqrt{\Delta t} + \frac12\sigma^2 \Delta t$$

로 근사할 수 있습니다. 그런데 위 식의 우변은 각각의 부호에 대해 

$$ e^{\sigma \sqrt{\Delta t}} , e^{-\sigma \sqrt{\Delta t}}$$

의 근사치이므로 결론적으로

$$ u = e^{\sigma \sqrt{\Delta t}} , d= e^{-\sigma \sqrt{\Delta t}} \tag{8}$$

라 놓을 수 있습니다.

 

$u, d$의 값은?(근사치)

$$ u = e^{\sigma \sqrt{\Delta t}} ~, ~d= e^{-\sigma \sqrt{\Delta t}}$$

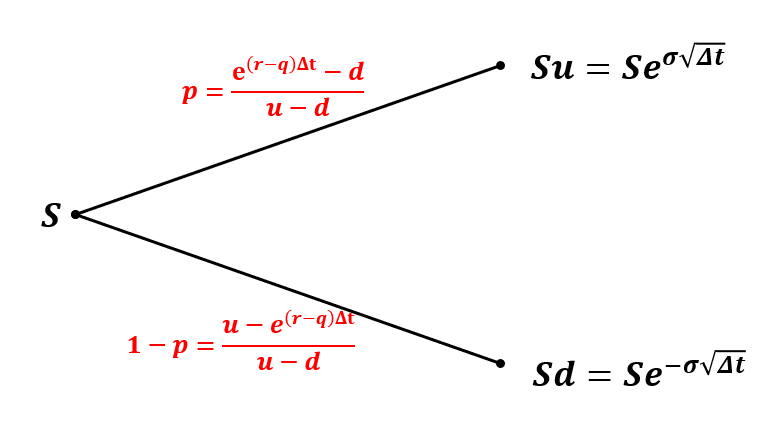
이 내용을 그림으로 정리하면 다음과 같습니다.

 

 

근사치도 괜찮은가?

원래 $u,d$는 

$$ x^2 -\left( e^{(r-q+\sigma^2 )\Delta t}  + e^{-(r-q)\Delta t} \right)x +1 =0$$

의 두 근이라고 설명했습니다. 이것의 근삿값이 식(8)인 거죠. 둘 사이에 큰 차이가 없는지 살펴봐야겠습니다.

 

import numpy as np


def test_binomial_updown_rario():
    r, q = 0.02, 0.05
    sigma = 0.2
    dt = 1

    A = np.exp((r - q + sigma ** 2) * dt) + np.exp(-(r - q) * dt)
    u_qf = 0.5 * (A + np.sqrt(A ** 2 - 4))
    d_qf = 0.5 * (A - np.sqrt(A ** 2 - 4))

    u_aprx, d_aprx = np.exp(sigma * np.sqrt(dt)), np.exp(-sigma * np.sqrt(dt))

    print('Quadratic formula : u is {:.3f}, d is {:.3f}'.format(u_qf, d_qf))
    print('Appoximation      : u is {:.3f}, d is {:.3f}'.format(u_aprx, d_aprx))


if __name__ == '__main__':
    test_binomial_updown_rario()

 

code에 특히 설명할 부분이 없어 넘어가겠습니다.  결과를 보시죠.

Quadratic formula : u is 1.223, d is 0.818
Appoximation      : u is 1.221, d is 0.819

Process finished with exit code 0

$\Delta t =1$이라고 아주 크게 작아도,  $u, d$가 제대로 근사가 되어 있음을 볼  수 있죠. 보통 실전에서는 

$$\Delta t = \frac1{365}$$ 로 잡습니다. 이것이 1일을 뜻하기 때문이죠. 그럼 하루에 대해서 dt =1/365로 바꾸어 결과를 보면

 

Quadratic formula : u is 1.011, d is 0.990
Appoximation      : u is 1.011, d is 0.990

Process finished with exit code 0

거의 일치한다고 보면 됩니다. 따라서 근사치 $u,d$를 써도 값에는 거의 영향을 끼치지 않을 것 같습니다.

 

주가 모델을 이항 분포로 접근한 모델은 1970년대 개발된 모형입니다. 소위 CRR 모델이라는 것인데요, 위의 논리와 참 비슷하나 약간의 차이가 있습니다. 역사적으로 중요한 모델이니 위의 내용과 어떠한 점이 다른지, 결과는 비슷한지에 대해 다음 글에서 소개해 보도록 하겠습니다.