Binomial Tree #3 : 이항모델 가지치기

 

 

이 글은

2022.08.09 - [금융공학] - Binomial Tree #2: CRR 모델이란?

Binomial Tree #2: CRR 모델이란?

에서 이어집니다. 지난 글에서는 GBM 주가모형이 아닌, GBM가 평균과 분산이 같아지는 이항 모형(binomial model)을 소개했었습니다. 복습을 해 볼까요?

 

이항 모델 복습

그림으로 한번에 정리해보면 다음과 같습니다.

 

 

 

• 주가는 $u$ 의 상승률로 오르거나(확률 $p$), $d$의 하락률로 내리는(확률 $1-p$) 두 가지 경우이다.
• 주가가 상승했다가 하락하면, 또는 하락했다가 상승하면 자기 자신으로 돌아온다. 즉 $ud=1$이다.
• GBM 주가 모델의 기댓값과 분산이 설명되도록 $u, d$와 확률 $p$를 결정한다.

결과는 아래와 같습니다.

up &down 확률
$$ \begin{align} p &= \frac{e^{(r-q)\Delta t}-d}{u-d}\\ 1-p &= \frac{u-e^{(r-q)\Delta t}}{u-d} \\ \end{align} $$

$u, d$의 값
$$ u = e^{\sigma \sqrt{\Delta t}} ~, ~d= e^{-\sigma \sqrt{\Delta t}}$$

 

트리 만들기

이항 모델은 짧은 간격 $\Delta t$사이에 벌어지는 일을 모델링한 것입니다. 그렇다면 일반적인 경우는 어떨까요? 만기까지 $T$ 시간이 남았을 때, 주가는 과연 어떻게 행동할까요?

 

현재 시점 $t=0$에서 $T$까지를 잘게 균등하게 쪼개어 각 시간 간격이 $\Delta T$가 되게 합시다. 아니면, 

$[0,T]$ 사이를 $N$등분하여 

$$ \Delta t = \frac{T}{N}$$

이라 놓아도 되죠. $N$이 커지면 $\Delta t$는 충분히 작아질 것입니다. 그러면

$$ 0=t_0<t_1<t_2<\cdots <t_{N-1}<t_{N}=T$$ 가 되고, $\Delta t= t_{i+1}-t_i$일 것입니다. 

 

각 시점에 다음과 같은 가지치기를 해 보죠.

 

$t_0$ 시점에서의 가지치기

시점 $t=0$에서 두 갈래로 뻗어나가는 가지들

 

 

$t_1$에서의 가지치기

$Su$에서 뻗어나가는 가지

 

$Sd$에서 뻗어나가는 가지

 

 

$t_2$에서의 가지치기

제일 위에 가지가 뻗어나간다. 파란색 음영은 가지가 만나는 모습

중간 가지가 뻗어나간다. 파란색 음영은 가지가 만나는 모습

 

 

제일 아래 가지까지 완성하여 $t_2$에서 뻗어나가는 가지까지 완성

 

 

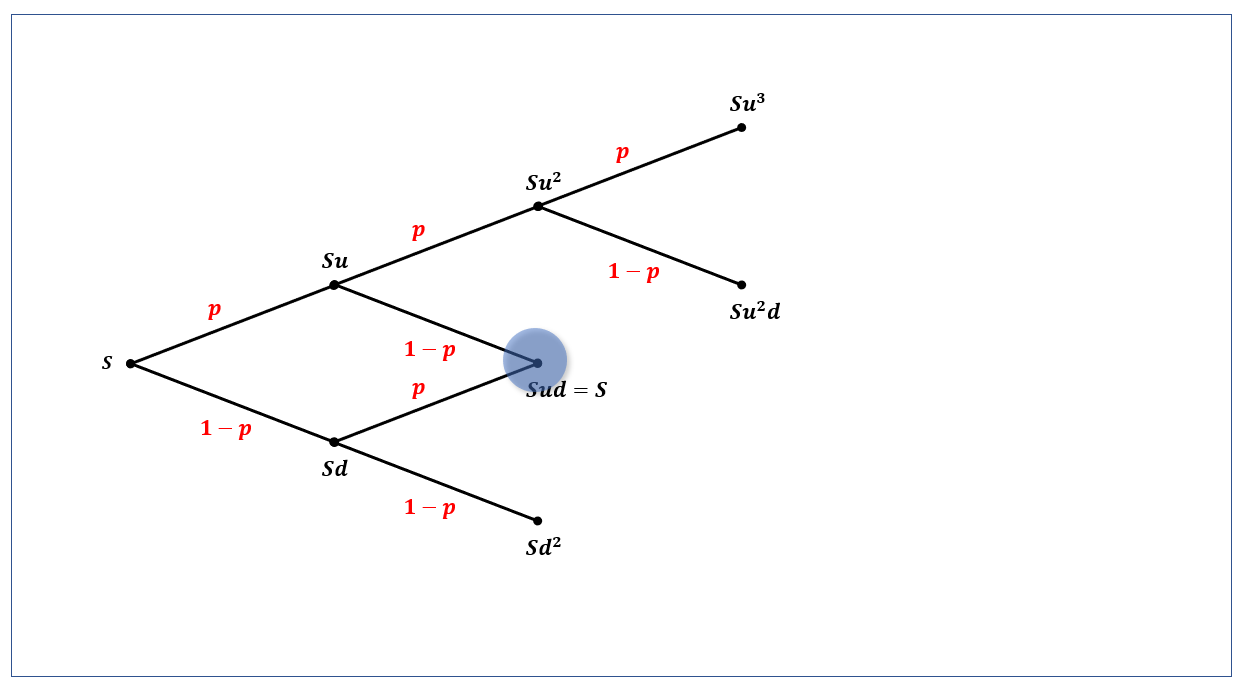
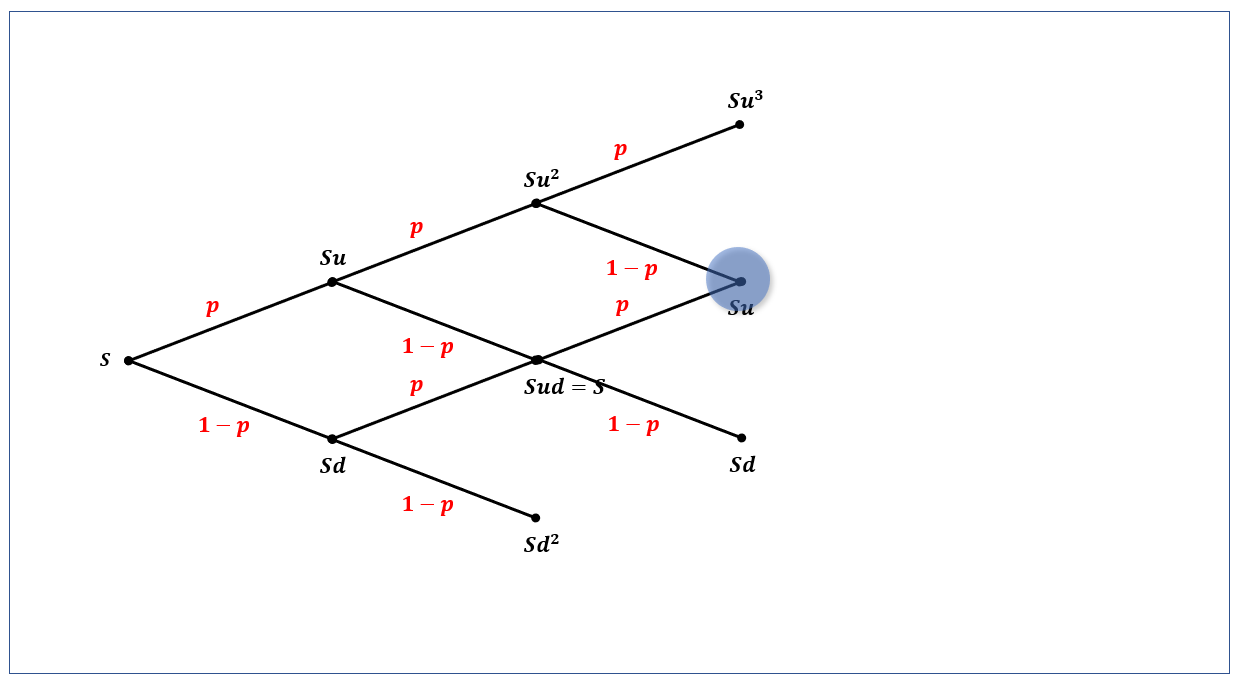
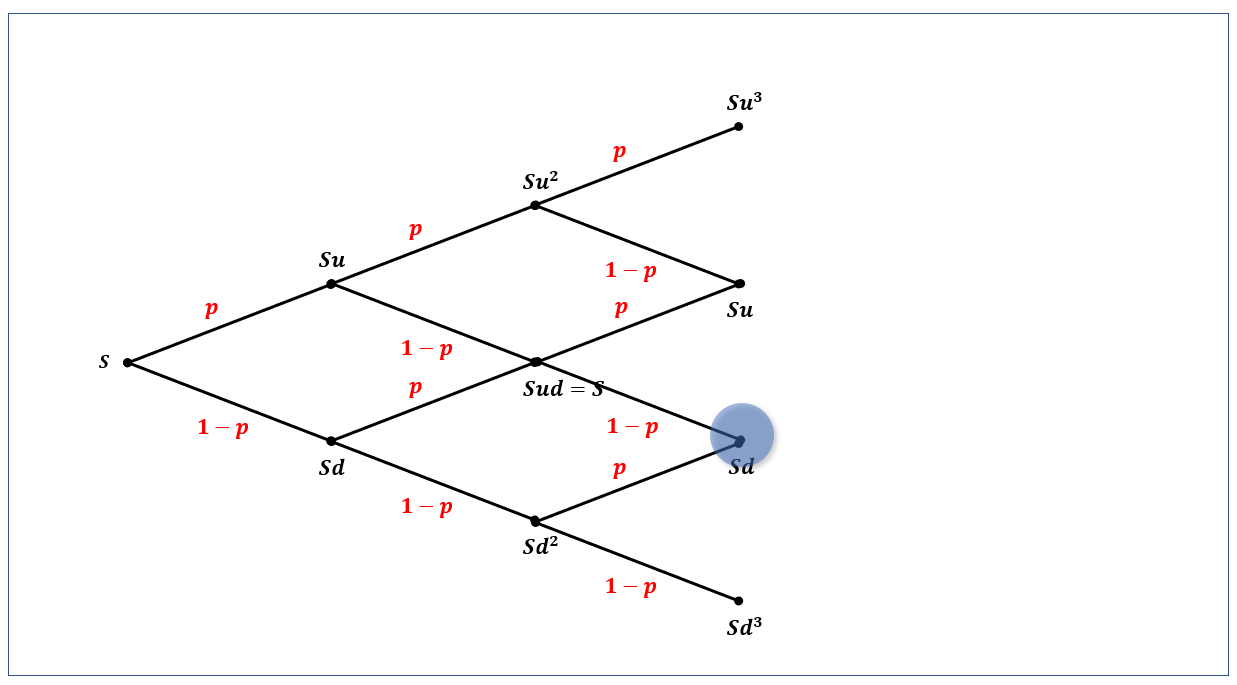
이렇게 가지가 뻗어나가는 형태로 주가가 흘러가는 모델이라 하여 해당 모델을 이항 트리(binomial tree)라고 부릅니다.

용문산 정상의 은행나무 모형과 닮은듯?

 

 

파이썬으로 Binomial Tree 그리기

 

이항 모델을 이어 붙여 Binomial Tree가 어떻게 생성되는지 python으로 코딩을 해보겠습니다.

 

import numpy as np
import matplotlib.pyplot as plt
import random

def draw_binomial_tree():
    sigma = 0.2
    dt = 1 / 365

    u = np.exp(sigma * np.sqrt(dt))
    d = 1 / u

    nNode = 5

    for n in range(nNode):
        for i in range(n + 1):
            s = u ** i * d ** (n - i)
            x = [n, n + 1]
            y_up = [s, s * u]
            y_down = [s, s * d]
            plt.xlim(-1, nNode + 1)
            plt.ylim(0.9, 1.1)
            plt.plot(x, y_up, color='gray', marker='o')
            plt.plot(x, y_down, color='gray', marker='o')
            plt.pause(0.5)

    for n in range(nNode + 1):
        for i in range(n + 1):
            s = u ** i * d ** (n - i)
            plt.text(n, s, '$u^{}d^{}$'.format(i, n - i))
    plt.pause(1)
    xPath = []
    yPath = []
    s0 = 1
    for n in range(nNode + 1):
        if n == 0:
            s0 = 1
        else:
            s0 *= random.choice([u, d])
        yPath.append(s0)
        xPath.append(n)

    plt.plot(xPath, yPath, color='r', marker='s', linewidth=4)
    plt.pause(3)
    plt.show()

if __name__ == '__main__':
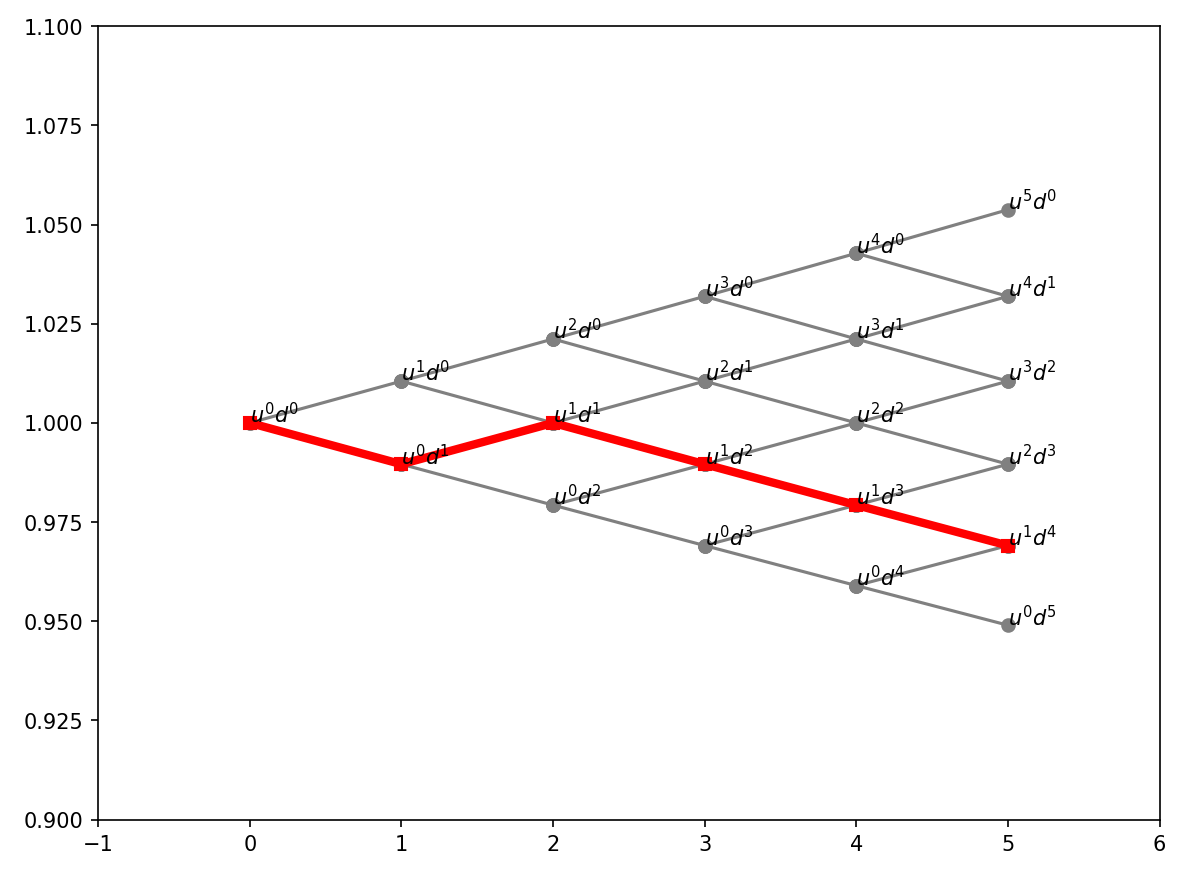
    draw_binomial_tree()

시간축을 5 등분한 트리를 그린 코딩입니다. 트리가 완성되어 가는 과정을 볼 수 있습니다. 

 

각 노드에 해당하는 주가를 기재하였고, 현재 시점부터 만기 때까지 움직인 실제 주가 패스 하나를 빨간색으로 표시해 놓았습니다. 참고로 주가 패스를 하나 만드는 방법은 아래 부분입니다.

 

    xPath = []
    yPath = []
    s0 = 1
    for n in range(nNode + 1):
        if n == 0:
            s0 = 1
        else:
            s0 *= random.choice([u, d])
        yPath.append(s0)
        xPath.append(n)

    plt.plot(xPath, yPath, color='r', marker='s', linewidth=4)

 

 

 

트리가 가지치기 하는구나~

 

빨간선은 현재시점부터 만기까지 주가가 움직일 법한 자취이 한 예제

 

 

다음 글에서는 이 트리를 가지고 어떻게 파생상품의 값을 구할 수 있는지 그 원리를 알아보겠습니다.