파생상품의 가격 결정: binomial tree를 이용해 봅시다.

 

 

이 글에서는 

2022.08.11 - [금융공학] - Binomial Tree #3 : 이항 모델 가지치기

Binomial Tree #3 : 이항모델 가지치기

에 등장하는 binomial tree를 사용하여 파생상품의 가격을 구해보도록 하겠습니다. 지겹더라도 이항 트리의 단위 원소 격인 이항 모델을 복습해 보기로 하죠.

 

이항 모델 복습

주식은 상승(상승률 $u$), 하락(하락률 $d$) 두 가지 상태이고, $ud=1$ 을 만족하며 GBM의 기댓값과 분산을 만족하도록 상승확률 $p$와 하락 확률 $1-p$를 설계하며 다음과 같았습니다.

 

너무 지겹게 등장해, 이제 외울떄도 될만한 그림

 

up &down 확률
$$\begin{align} p &= \frac{e^{(r-q)\Delta t}-d}{u-d}\\ 1-p &= \frac{u-e^{(r-q)\Delta t}}{u-d} \\ \end{align}$$

$u, d$의 값
$$u = e^{\sigma \sqrt{\Delta t}} ~, ~d= e^{-\sigma \sqrt{\Delta t}}$$

 

 

파생상품 가격결정 조건

일단 binomial tree의 하나 단위인 이항 모델 단위에서 벌어지는 일을 살펴봅시다. 다음의 그림을 봅시다.

 

파생상품과 주식으로 구성된 포트폴리오

 

파생상품 $F(t,S_t)$의 시점 $t$에서의 가격을 $f$, 시점 $t+\Delta t$에서의 가격을

기초자산	$Su$	$Sd$
파생상품의 가격	$F(t+\Delta t, Su)$	$F(t+\Delta t, Sd)$
기호	$f_u$	$f_d$

라 합시다. 그리고  다음과 같은 포트폴리오를 구성해봅시다(포트폴리오의 구성은 2022.08.02 - [금융공학] - 파생상품 가격 결정 Black Scholes Equation에서 다뤘던 것과 똑같습니다. 참고해 보세요)

 

파생상품 하나와 적절한 갯수($\alpha$)의 기초자산을 섞어서 포트폴리오를 구성하는 이유는 위, 아래 어느 방향으로 튈지 모르는 기초자산의 움직임으로 인해 파생상품 가격이 흔들리는 것을 방지(헤지) 하기 위함입니다.

 

포트폴리오의 구성
파생상품	1개
기초자산 계약	$\alpha$개

 

따라서, 시점 $t$에서의 포트폴리오의 가치를 $\pi(t)$라 하면,

$$\pi(t) = F(t,S_t) + \alpha S_t = f+ \alpha S\tag{1}$$

입니다.

 

이것이 $t+\Delta t$시점이 되면 두 가지 경우가 되겠죠.

주가 상승 시,

$$\pi(t+\Delta t) = F(t+\Delta t, S_{t+\Delta t} )+\alpha S_{t+\Delta t} = f_u +\alpha Su\tag{2}$$
이거나 주가 하락시,
$$\pi(t+\Delta t) = F(t+\Delta t, S_{t+\Delta t} )+\alpha S_{t+\Delta t} = f_d +\alpha Sd\tag{3}$$ 입니다. 

지금 이 포트폴리오의 목적은 파생상품을 기초자산인 주식으로 헤지하여 불확실성을 잡는데 목적이 있습니다. 이런 목적에서 봤을 때, 식(2)과 (3)는 값이 똑같게 나와야 합니다 (만일 다르다면, 주가의 움직임에 따라 포트폴리오의 값에 불확실이 생겨버리죠)

따라서

$$f_u +\alpha Su = f_d +\alpha Sd \tag{4}$$

를 만족합니다.

즉

$$\alpha = -\frac{f_u-f_d}{(u-d)S}\tag{5}$$

입니다(나중에 자세히 설명할 기회가 있겠지만, $\alpha$를 델타(delta)라 부릅니다.)

식(4)에 식(5)을 대입하여 $t+\Delta t$시점에서의 포트폴리오의 가치를 구하면

$$\pi(t+\Delta t) = \frac{uf_d-df_u}{u-d}\tag{6}$$

입니다.

 

그런데 이 포트폴리오는 기초자산을 포함하고 있고, 이 기초자산에서 연속 배당 $d$인 배당이 발생합니다. 구체적으로 $\Delta t$시간 동안 발생하는 배당의 양은 

$$d\cdot \alpha  S \Delta t$$

입니다. 따라서 포트폴리오의 변화는

$$\Delta \pi(t) + d\alpha  S \Delta t$$

입니다. 이 변화분은 arbitrage 가 없기 위해서, 즉 공짜 점심이 없기 위해서 이 값은

$$r\pi(t) \Delta t$$

와 동일해야 하죠( $r$은 무위험 이자율.) 정리하면

 

$$\Delta \pi(t) + d\alpha  S \Delta t =  r\pi(t) \Delta t$$

 

$\Delta \pi(t)= \pi(t+\Delta t)-\pi(t)$ 이므로 위 식에 넣어 정리하면

 

$$\pi(t+\Delta t) = (1+ r\Delta t) \pi(t) -d\alpha S \Delta t\tag{7}$$

입니다. 식(7)에 식(1), (6)을 넣어 정리하는 일만 남았습니다.

 

$$\begin{align} f_u +\alpha Su &= (1+r\Delta t)(f+\alpha S) -d\alpha S\Delta t\\ &= (1+r\Delta t) f + \alpha S(1+(r-d)\Delta t)\\ & \approx e^{r\Delta t} f +\alpha S e^{(r-d)\Delta t} \tag{8} \end{align}$$

마지막으로 식(8)을 $f$에 대해 정리해 보면

 

$$\begin{align} f & = e^{-r\Delta t} \left[ f_u +\alpha Su -\alpha S e^{(r-d)\Delta t}\right]\\ & =e^{-r\Delta t} \left[ f_u - \frac{f_u-f_d}{(u-d)S} S(u-e^{(r-d)\Delta t})\right]\\ & = e^{-r\Delta t} \left[ \frac{e^{(r-d)\Delta t}-d}{u-d} f_u + \frac{u-e^{(r-d)\Delta t}}{u-d} f_d \right]\\ & = e^{-r\Delta t} \left[ p f_u + (1-p)f_d\right] \end{align}$$

 

우변을 보면 시점 $t+\Delta t$의 파생상품이 가질 수 있는 두 변수 $f_u, f_d$에 대한 기댓값입니다. 그걸 $\Delta t$만큼 할인한 것이 바로 $f$이죠. 일견 당연해 보이는 결과입니다. 너무나 중요한 결론이므로 다시 한번 강조해서 쓰겠습니다.

이항 모형 하에서 파생상품의 가격 결정 조건

$$f= e^{-r\Delta t} \left[ p f_u + (1-p)f_d\right] \tag{*}$$

이제 남은 것은 binomial tree에서 파생상품의 가치를 구하는 것입니다. 어떻게 구할 수 있을까요?

 

 

 

파생상품의 가격 계산

바로, binomial tree의 마지막 잔가지로부터 거꾸로 내려오는 겁니다. 파생상품의 만기 페이오프는 이미 정해져 있습니다. 즉, 

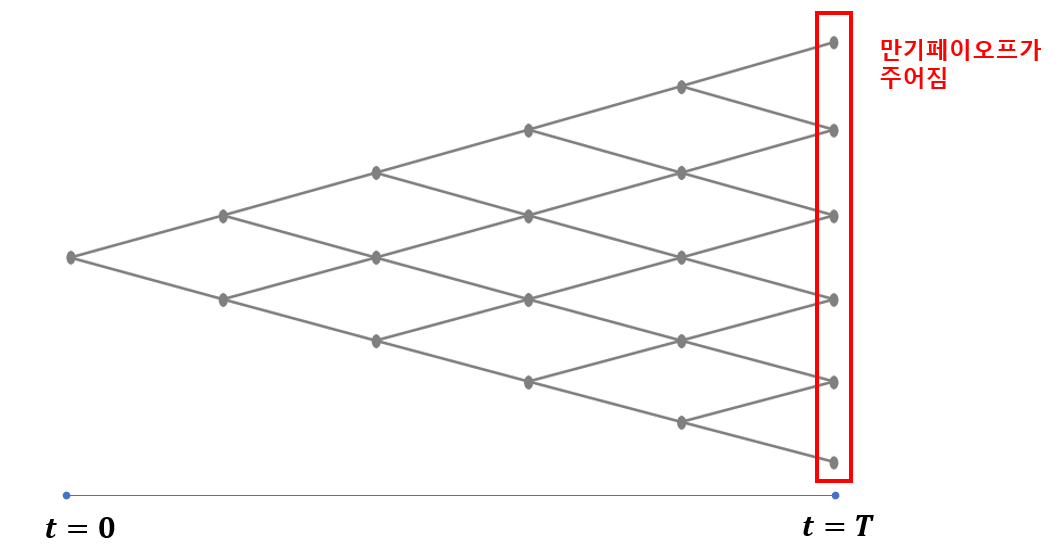
빨간색 영역의 점들이 다 알려져 있는 거죠. 그럼 바로 전 단계 노드는 식(*)에 의해 구할 수 있습니다.

 

 

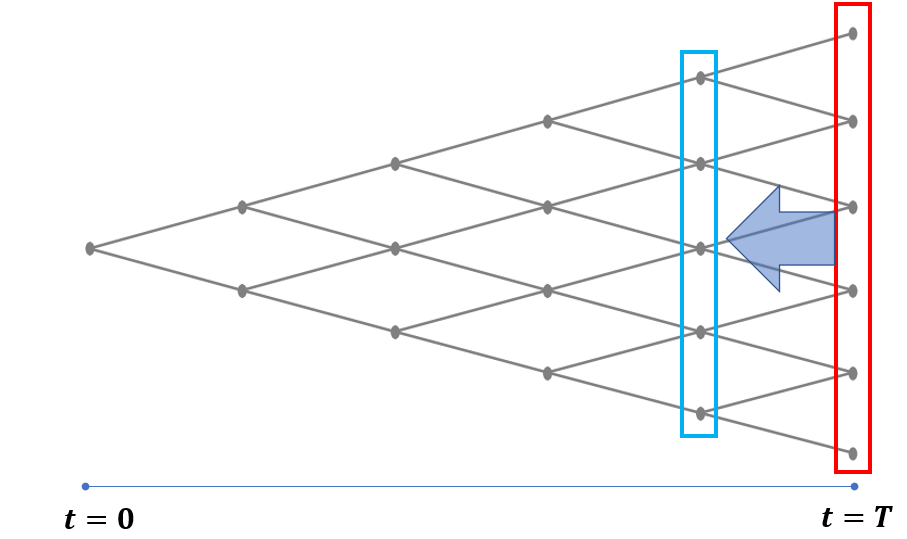
이렇게 처음으로 내려오다 보면,

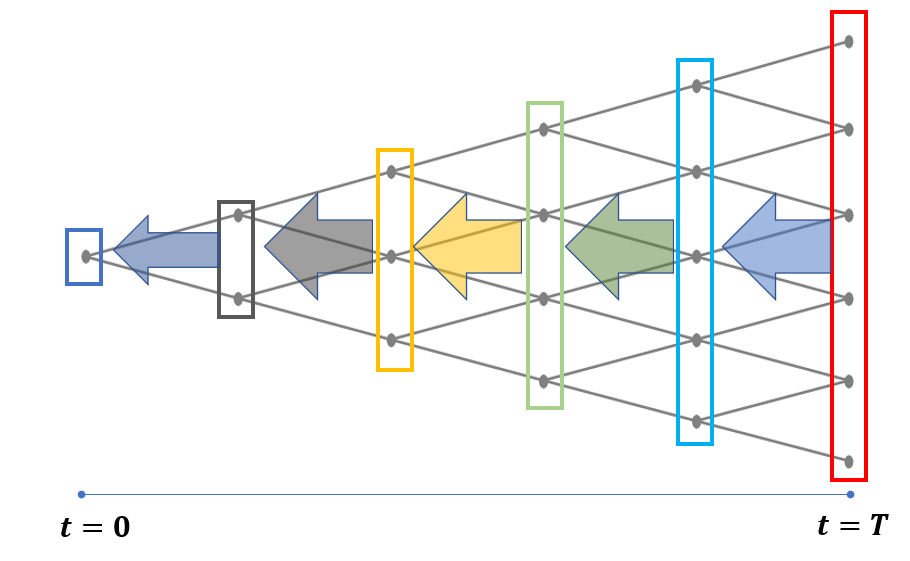
끝까지 내려오겠지요. 이 끝점이 바로 파생상품의 현재가치

$$F(0,S)$$

가 되는 것입니다.

 

 

수식으로 표현

수식으로 표현해 볼까요?  시점 step $n$번째의 아래서부터 $i$번째 노드는 기초자산의 가격이

$$S_0 u^{i}d^{n-i}$$

입니다. 이때의 파생상품의 가격을 

$$f(n,i), 0\leq n\leq N, 0\leq i\leq N$$

라 쓰면

$$f(n,i) = e^{-r\Delta t} \left[ p f(n+1,i+1) + (1-p) f(n+1,i)\right]$$

가 되는 것입니다. 그리고

$$f(N,i)$$

는 만기 때 페이오프로 알려져 있는 것이고요. 따라서 재귀적(recursive formula)으로 모든 $f(n,i)$를 다 구할 수 있는 것이죠.

 

 

 

 

 

다음 글에서는 python과 엑셀 VBA 등 프로그래밍 언어를 통해 파생상품의 가격을 결정하는 방법을 알아보겠습니다.