이 글은
2022.08.13 - [금융공학] - 파생상품의 가격 결정: binomial tree로 델타원상품 가격 구하기
파생상품의 가격 결정: binomial tree로 델타원상품 가격 구하기
이 글에서는 2022.08.12 - [금융공학] - 파생상품의 가격 결정: binomial tree를 이용해 봅시다. 파생상품의 가격 결정: binomial tree를 이용해 봅시다. 이 글에서는 2022.08.11 - [금융공학] - Binomial Tree #3..
sine-qua-none.tistory.com
에서 이어집니다.
지난 글에서는 python code로 델타원 상품의 가격결정을 해봤습니다.
binomial tree는 그 결과도 중요하지만 tree의 가지가 뻗어나가는 모습을 visualizing 하는 것도 제법 재미가 있습니다. 엑셀 기반의 프로그래밍 언어인 VBA를 사용하여 binomial tree를 구현해 보도록 하겠습니다.

VBA Code
다음의 코드를 보겠습니다.
Option Explicit
Option Base 1
Type treeNode
underlying_value As Double
pv As Double
step As Integer
upcnt As Integer
underlying_xpos As Integer
underlying_ypos As Integer
pv_xpos As Integer
pv_ypos As Integer
End Type
Function payoff(s As Double) As Double
payoff = s
End Function
Sub test_binomial_tree()
Dim s0 As Double
Dim r As Double, q As Double, sigma As Double, maturity As Double
Dim ntimeSteps As Integer
Dim dt As Double
Dim u As Double, d As Double
Dim p As Double
Dim a As Double
s0 = 100
r = 0.02
q = 0.01
sigma = 0.2
maturity = 1
ntimeSteps = 10
dt = maturity / ntimeSteps
u = Exp(sigma * Sqr(dt))
d = 1 / u
a = Exp((r - q) * dt)
p = (a - d) / (u - d)
Dim nodes() As treeNode
ReDim nodes(0 To ntimeSteps, 0 To ntimeSteps)
Dim n As Integer, i As Integer
Dim sVal As Double
Dim df As Double
df = Exp(-r * dt)
With Range("A1").Resize(1000, 1000)
.ClearContents
.Interior.Color = xlNone
End With
For n = ntimeSteps To 0 Step -1
For i = 0 To n
sVal = s0 * (u) ^ (i) * (d) ^ (n - i)
nodes(n, i).underlying_value = sVal
nodes(n, i).step = n
nodes(n, i).upcnt = i
nodes(n, i).underlying_xpos = 2 * n
nodes(n, i).underlying_ypos = -4 * i + 2 * n
nodes(n, i).pv_xpos = 2 * n
nodes(n, i).pv_ypos = -4 * i + 2 * n + 1
If n = ntimeSteps Then
nodes(n, i).pv = payoff(sVal)
Else
nodes(n, i).pv = df * (p * nodes(n + 1, i + 1).pv + (1 - p) * nodes(n + 1, i).pv)
End If
Next i
Next n
Dim orng As Range
Set orng = Cells(3 * ntimeSteps, "C")
For n = 0 To ntimeSteps
For i = 0 To n
orng.Offset(nodes(n, i).underlying_ypos, nodes(n, i).underlying_xpos) = nodes(n, i).underlying_value
orng.Offset(nodes(n, i).underlying_ypos, nodes(n, i).underlying_xpos).Interior.ColorIndex = 35
orng.Offset(nodes(n, i).pv_ypos, nodes(n, i).pv_xpos) = nodes(n, i).pv
orng.Offset(nodes(n, i).pv_ypos, nodes(n, i).pv_xpos).Interior.ColorIndex = 40
Next i
Next n
End Sub
코드를 간단히 살펴보겠습니다.
Option Explicit '변수를 명시적으로 선언할 것을 요청함. 에러를 방지할 목적
Option Base 1 '배열의 index를 1부터 시작
Type treeNode 'treeNode라는 구조체 선언
underlying_value As Double 'node의 기초자산 가격을 뜻하는 member
pv As Double 'node에서의 파생상품의 가치
step As Integer 'node가 속하는 timestep
upcnt As Integer 'node의 기초자산 가격에 u가 미치는 영향 S=u^i d^(n-i)의 i
underlying_xpos As Integer '(0,0)node 에서 상대적으로 기초자산 가격을 print할 cell의 위치(x 방향)
underlying_ypos As Integer '(0,0)node 에서 상대적으로 기초자산 가격을 print할 cell의 위치(y 방향)
pv_xpos As Integer '(0,0)node 에서 상대적으로 파생상품 가격을 print할 cell의 위치(x 방향)
pv_ypos As Integer '(0,0)node 에서 상대적으로 파생상품 가격을 print할 cell의 위치(y 방향)
End Type○ binomial tree에는 노드가 많이 등장하고, 노드마다 기억해야 할 값들이 많아서 이렇게 구조체로 선언하면 편합니다.
Function payoff(s As Double) As Double '만기 payoff를 뜻하는 함수
payoff = s '기초자산 자기자신을 만기 payoff로, 즉 delta one 상품
End Function
Sub test_binomial_tree() #실제 실행될 프로시저
...
end Sub
Dim s0 As Double
Dim r As Double, q As Double, sigma As Double, maturity As Double
Dim ntimeSteps As Integer
Dim dt As Double
Dim u As Double, d As Double
Dim p As Double
Dim a As Double
s0 = 100 '기초자산 현재가격
r = 0.02 '무위험 이자율
q = 0.01 '연속배당률
sigma = 0.2 '기초자산 변동성
maturity = 1 '만기
ntimeSteps = 10 '만기를 10등분
dt = maturity / ntimeSteps '각 등분된 시점별 간격
u = Exp(sigma * Sqr(dt)) '기초자산의 상승률
d = 1 / u '기초자산의 하락률
a = Exp((r - q) * dt)
p = (a - d) / (u - d) '기초자산이 S에서 Su로 상승할 확률
df = Exp(-r * dt) '한 단위 시간 간격동안 적용되는 할인율
With Range("A1").Resize(1000, 1000) ' 제일 상단 왼쪽 cell을 기준으로 행, 열 각 1000개인 영역을 선택하여
.ClearContents ' 내용을 모두 지우고
.Interior.Color = xlNone ' 셀의 색을 채우기 없음으로 선택
End With
For n = ntimeSteps To 0 Step -1 'timestep을 만기(N)부터 현재(0)까지 1씩 감소시키고
For i = 0 To n '각 timestep의 i번째 주가 level에 대해
sVal = s0 * (u) ^ (i) * (d) ^ (n - i) '주가 u^i d^(n-i)
nodes(n, i).underlying_value = sVal 'node의 underlying_value 멤버에 주가 대입
nodes(n, i).step = n 'node의 step 멤버에 n
nodes(n, i).upcnt = i 'node의 upcnt 멤버에 i
nodes(n, i).underlying_xpos = 2 * n '기초자산 가격 display는 한 열 건너 하나씩
nodes(n, i).underlying_ypos = -4 * i + 2 * n '기초자산 가격 display의 행 방향 위치
nodes(n, i).pv_xpos = 2 * n
nodes(n, i).pv_ypos = -4 * i + 2 * n + 1
If n = ntimeSteps Then
nodes(n, i).pv = payoff(sVal) '만기 시점에는 payoff 함수의 값으로
Else
nodes(n, i).pv = df * (p * nodes(n + 1, i + 1).pv + (1 - p) * nodes(n + 1, i).pv)
'만기 시점이 아닐 경우 binomial tree node가 만족하는 점화식으로
End If
Next i
Next n
Set orng = Cells(3 * ntimeSteps, "C") ' display 기준이 될 셀을 하나 정하고(C열의 적절한 행)
For n = 0 To ntimeSteps
For i = 0 To n
orng.Offset(nodes(n, i).underlying_ypos, nodes(n, i).underlying_xpos) = nodes(n, i).underlying_value
orng.Offset(nodes(n, i).underlying_ypos, nodes(n, i).underlying_xpos).Interior.ColorIndex = 35
orng.Offset(nodes(n, i).pv_ypos, nodes(n, i).pv_xpos) = nodes(n, i).pv
orng.Offset(nodes(n, i).pv_ypos, nodes(n, i).pv_xpos).Interior.ColorIndex = 40
Next i
Next n
' 기준셀에 Offset함수를 사용하여 상대 행, 상대열을 지정하고 그 위치에 값을 찍는다.
' 기초자산 가격의 cell은 colorindex = 35(연두색계열), 파생상품의 가격 cell은 colorindex = 40○ colorindex 색깔은 다음의 그림을 참고해보세요.

해당 프로시저를 실행한 결과는 아래와 같습니다.
결과
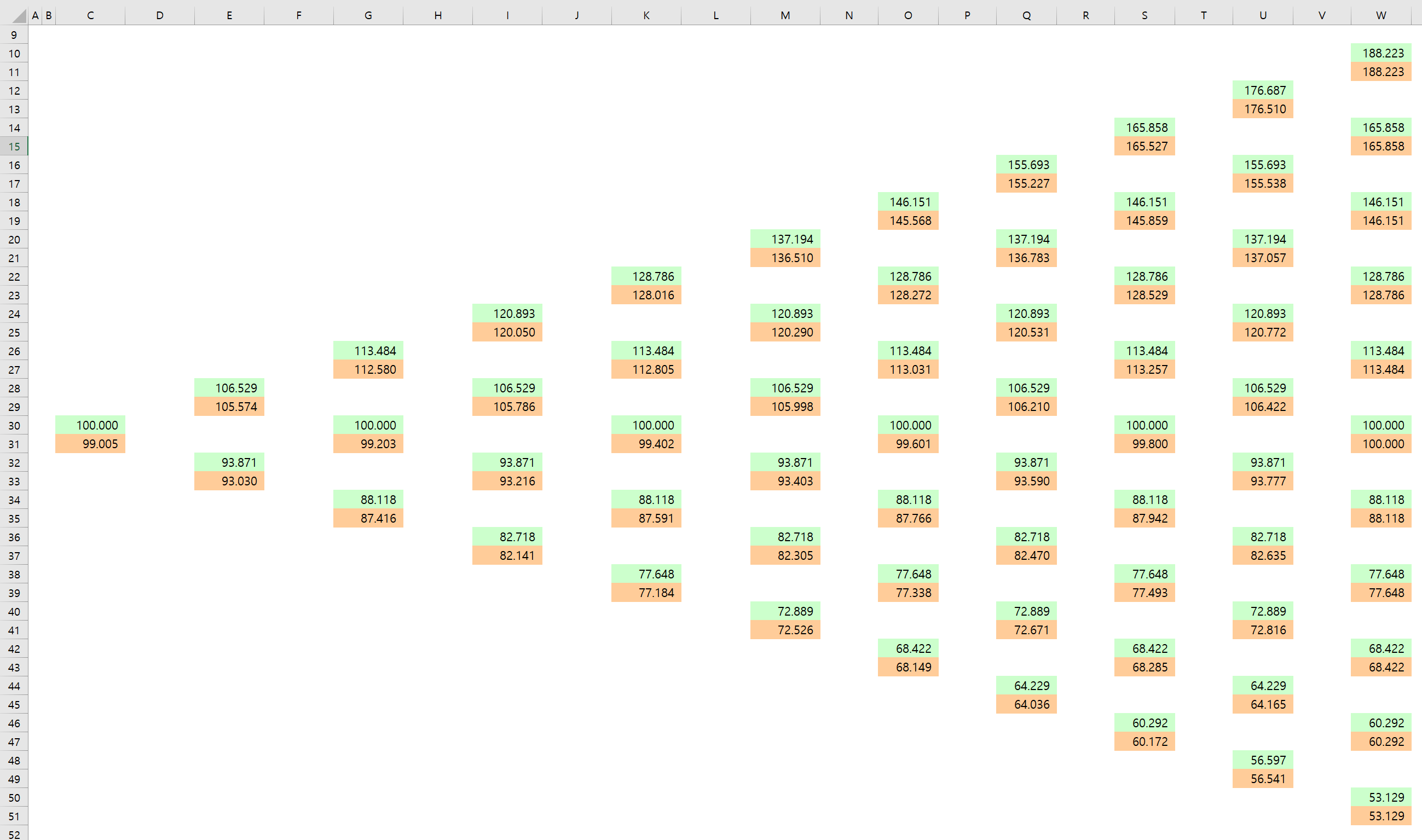
연두색 cell (colorindex 35)이 주가, 주황색 cells (color index 40)이 파생상품의 가치입니다.
제일 오른쪽은 델타원 상품의 특성상 연두색 cell과 주황색 cell의 값이 같죠. 그게 재귀적으로 왼쪽으로 이동하면서 계산이 됩니다.
결국 제일 왼쪽의 주황색 cell이 파생상품의 현재가치가 되는 것이고, 이것은 정확히
$$S_0 e^{-dT}$$
로 구한 값과 일치합니다.
첨부파일을 올려놓도록 하겠습니다. 한번 검증해 보시기 바랍니다.
'금융공학' 카테고리의 다른 글
| 옵션 #2. 옵션 프리미엄 구하기(Closed form) (0) | 2022.08.17 |
|---|---|
| 옵션 #1. 옵션이란? 옵션의 유명한 관계식이 있다던데.. (2) | 2022.08.17 |
| 파생상품의 가격 결정: binomial tree로 델타원상품 가격 구하기 (0) | 2022.08.13 |
| 파생상품의 가격 결정: binomial tree를 이용해 봅시다. (0) | 2022.08.12 |
| Binomial Tree #3 : 이항모델 가지치기 (0) | 2022.08.11 |



댓글