GBM 모델은 다음과 같습니다.
무위험 이자율을 r, 연속배당률을 q라 하면
dSt/St=(r−q)dt+σdWt
어떤 시간 간격 Δt에 대해 시점 t와 시점 t+Δ 사이의 주가의 관계식은
St+Δt=Stexp((r−q−12σ2)Δt+σWΔt)
St가 결정되어 있을 때, St+Δt를 결정하는 것은 다름아닌 WΔt이죠. 이것은 정규분포 N(0,√Δt2)을 따르기 때문에 St+Δt가 나오는 건, 시쳇말로 무한개갰죠. 연속확률분포니까요.
Motivation
이것을 좀 더 간단화시켜, 기초자산 St가 일정 비율 오르고(up), 일정 비율 내리는(down) 모델을 생각해 봅시다.
상승 비율을 u, 하락비율을 d라 하고, S를 상승했을 때, S⋅u, 하락했을 때, S⋅d 두 경우로 가정합니다. 그리고 상승확률을 p, 하락 확률을 1−p라 합시다. 표로 정리하면 이렇습니다.
현재 주가를 S라 할 때,
| 상태 | up | down |
| 변수 | S⋅u | S⋅d |
| 확률 | p | 1−p |

우리의 목적은 위 그림의 상승, 하락비율 u,d와 확률 p값을 찾는 것입니다. 하지만 아무렇게나 찾으면 안 되겠죠.
주가 S가 GBM 모델하에서 가지는 특징들을 유지할 수 있도록 만드는 것이 중요
합니다. 이제 분석을 해 볼까요?
참고로, 위의 모델을 변수가 2개의 값을 가진다고 해서 이항 모델 영어로는 binomial model이라고 합니다.
이항 모델이 만족할 조건
이항 모델이 다음의 성질을 만족했으면 좋겠습니다.
- 이항 모델은 최대한 간결하게!
- St+Δt의 기댓값이 GBM 모델에서의 기댓값과 같으면 좋겠다.
- St+Δt의 분산이 GBM 모델에서의 분산과 같으면 좋겠다.
1. 이항 모델의 간결성
이항 모델이 간결해지는 걸 위해 주가가 올라갔다 내려왔을 때, 자기 자신이 되는 세팅을 해 봅시다. 즉,
S=(Su)d=(Sd)u
를 원하므로
ud=1
이라 합시다.
2,3. 평균과 분산의 일치
우선 1,2번을 위해, 식 (GBM)에서 St+Δt의 기댓값과 2차 모멘텀(분산을 의미)을 구하면 다음과 같습니다.
E(St+Δt)=E[Stexp((r−q−12σ2)Δt+σWΔt)]=Ste(r−q)Δt
E(S2t+Δt)=E[S2texp(2(r−q−12σ2)Δt+2σWΔt)]=S2te(2r−2q+σ2)Δt
그런데, 이항 모델하에서 위 두식의 좌변을 보면, 짧은 시간의 변화 Δt 동안
St+Δt가 될 수 있는 값은 St⋅u,ST⋅d 두 가지이므로
pStu+(1−p)Std=E(St+Δt)=Ste(r−q)Δtp(Stu)2+(1−p)(Std)2=E(S2t+Δt)=Ste(2r−2q+σ2)Δt
입니다. 이것을 더 간단히 정리하면
pu+(1−p)d=e(r−q)Δtpu2+(1−p)d2=e(2r−2q+σ2)Δt
식(2),(3)을 각각 정리하면
(u−d)p+d=e(r−q)Δt(u2−d2)p+d2=e(2r−2q+σ2)Δt
입니다.
이항 모델의 계산
우선 식 (4)에서 두 확률을 구할 수 있습니다.
up &down 확률
p=e(r−q)Δt−du−d1−p=u−e(r−q)Δtu−d
이제, u,d만 결정되면 되겠죠.
식(4) ×(u−d)− 식(5)을 하면
1=e(r−q)Δt(u+d)−e(2r−2q+σ2)Δt
따라서
u+d=e(r−q+σ2)Δt+e−(r−q)Δt
을 만족합니다. 식(1)과 (6)을 종합하면
u,d 값은?
u,d는 2차 방정식
x2−(e(r−q+σ2)Δt+e−(r−q)Δt)x+1=0
의 두 근임. 그중 1보다 큰 값이 u, 작은 값이 d임
를 얻습니다. 그런데 식이 상당히 복잡합니다.
A=e(r−q+σ2)Δt+e−(r−q)Δt 라 하고 근의 공식을 쓰면
u=A+√A2−42d=A−√A2−42
입니다. 이 복잡한 식을 좀 깔끔하게 근사 시켜 볼까요?(어차피 정규분포를 이항으로 바꾼 과정 자체가 정확한 값이 아닌 근삿값을 허용한다는 뜻이므로 조금 더 깔끔하게 근사 시키는 것은 무리가 아니겠죠)
깔끔한 정리를 위하여 ex의 테일러 전개를 이용합니다.
ex=1+x+12!x2+13!x3+⋯
이제 A를 정리해 보면
A=e(r−q+σ2)Δt+e−(r−q)Δt=1+(r−q+σ2)Δt+1−(r−q)Δt+⋯=2+σ2Δt+Δt2(⋯)
Δt2이 무시할 정도로 작다고 하면, A=2+σ2Δt이고
A2−4=4σ2Δt+σ4Δt2≈4σ2Δt
이므로
u,d≈12(2+σ2Δt±√4σ2Δt)=1±σ√Δt+12σ2Δt
로 근사할 수 있습니다. 그런데 위 식의 우변은 각각의 부호에 대해
eσ√Δt,e−σ√Δt
의 근사치이므로 결론적으로
u=eσ√Δt,d=e−σ√Δt
라 놓을 수 있습니다.
u,d의 값은?(근사치)
u=eσ√Δt , d=e−σ√Δt
이 내용을 그림으로 정리하면 다음과 같습니다.
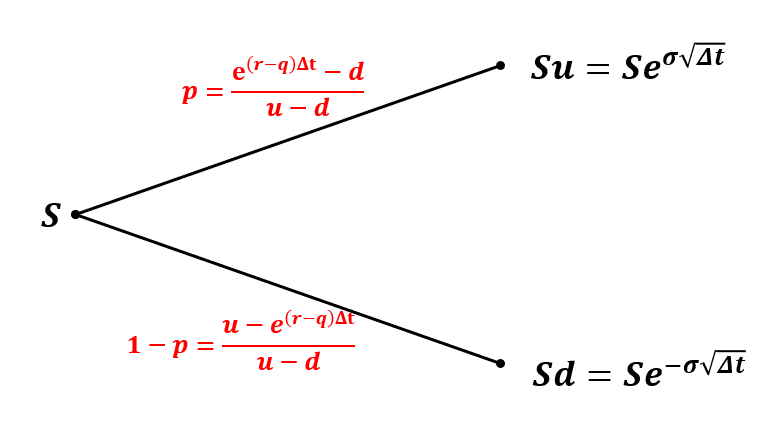
근사치도 괜찮은가?
원래 u,d는
x2−(e(r−q+σ2)Δt+e−(r−q)Δt)x+1=0
의 두 근이라고 설명했습니다. 이것의 근삿값이 식(8)인 거죠. 둘 사이에 큰 차이가 없는지 살펴봐야겠습니다.
import numpy as np
def test_binomial_updown_rario():
r, q = 0.02, 0.05
sigma = 0.2
dt = 1
A = np.exp((r - q + sigma ** 2) * dt) + np.exp(-(r - q) * dt)
u_qf = 0.5 * (A + np.sqrt(A ** 2 - 4))
d_qf = 0.5 * (A - np.sqrt(A ** 2 - 4))
u_aprx, d_aprx = np.exp(sigma * np.sqrt(dt)), np.exp(-sigma * np.sqrt(dt))
print('Quadratic formula : u is {:.3f}, d is {:.3f}'.format(u_qf, d_qf))
print('Appoximation : u is {:.3f}, d is {:.3f}'.format(u_aprx, d_aprx))
if __name__ == '__main__':
test_binomial_updown_rario()
code에 특히 설명할 부분이 없어 넘어가겠습니다. 결과를 보시죠.
Quadratic formula : u is 1.223, d is 0.818
Appoximation : u is 1.221, d is 0.819
Process finished with exit code 0Δt=1이라고 아주 크게 작아도, u,d가 제대로 근사가 되어 있음을 볼 수 있죠. 보통 실전에서는
Δt=1365 로 잡습니다. 이것이 1일을 뜻하기 때문이죠. 그럼 하루에 대해서 dt =1/365로 바꾸어 결과를 보면
Quadratic formula : u is 1.011, d is 0.990
Appoximation : u is 1.011, d is 0.990
Process finished with exit code 0거의 일치한다고 보면 됩니다. 따라서 근사치 u,d를 써도 값에는 거의 영향을 끼치지 않을 것 같습니다.
주가 모델을 이항 분포로 접근한 모델은 1970년대 개발된 모형입니다. 소위 CRR 모델이라는 것인데요, 위의 논리와 참 비슷하나 약간의 차이가 있습니다. 역사적으로 중요한 모델이니 위의 내용과 어떠한 점이 다른지, 결과는 비슷한지에 대해 다음 글에서 소개해 보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| Binomial Tree #3 : 이항모델 가지치기 (0) | 2022.08.11 |
|---|---|
| Binomial Tree #2: CRR 모델이란? (0) | 2022.08.09 |
| Black Scholes Equation의 풀이: 시뮬레이션 (0) | 2022.08.08 |
| Black Scholes Equation의 풀이: 델타원 상품 (0) | 2022.08.05 |
| Black Scholes Equation의 풀이: 확률프로세스를 이용하자. (2) | 2022.08.05 |



댓글