저번 글
2022.08.18 - [금융공학] - 옵션 #3. 옵션 프리미엄 구하기(FDM)
옵션 #3. 옵션 프리미엄 구하기(FDM)
지난 글 2022.08.17 - [금융공학] - 옵션 #2. 옵션 프리미엄 구하기(Closed form) 옵션 #2. 옵션 프리미엄 구하기(Closed form) 이번 글은 2022.08.17 - [금융공학] - 옵션 #1. 옵션이란? 옵션의 유명한 관계식이..
sine-qua-none.tistory.com
에서 유한차분법(FDM)으로 옵션의 가치를 구하는 방법에 대해 이론적인 내용을 알아봤습니다. 이제 프로그래밍을 통해 확인해 볼 차례인데요. 명시적 방법(explicit method)과 함축적 방법(implicit method) 중 명시적 방법을 사용하여 프로그래밍해보겠습니다.
명시적 FDM 복습
자세한 내용은 위의 링크를 참고하면 됩니다. 가볍게 결과를 정리해 보겠습니다.
○ 잔존만기 축 균등분할 현재 시점 t=0에서 만기시점 T까지 0=τ0<τ1<⋯<τN=T로 균등분할하고 k=τj+1−τj 로 간격을 구합니다.
○ 충분히 큰 Smax를 잡고 기초자산을 0=S0<S1<⋯<SJ=Smax 로 균등분할합니다. h=Sj+1−Sj 로 간격을 구합니다.
○ 콜옵션 가격 격자판 unj=U(τn,Sj) 를 생성하면, unj은 다음을 만족합니다.
○ 모든 j,n에 대하여 다음의 점화식을 만족한다.
1kun+1j=(−(r−q)Sj2h+σ2S2j2h2)unj−1+(1k−σ2S2jh2−r)unj+((r−q)Sj2h+σ2S2j2h2)unj+1
○ 초기조건 u0j=max
○ 경계조건 u_0^n = 2u_1^n-u_2^n~,~ u_{J}^n = 2u_{J-1}^n-u_{J-2}^n
Python Code
다음은 명시적 FDM으로 구현한 코드입니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
N = norm.cdf
def CallOptionBS(S, K, T, r, q, sigma):
if T == 0:
return np.max(S - K, 0)
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
return S * np.exp(-q * T) * N(d1) - K * np.exp(-r * T) * N(d2)
def Solve_BSEquation_1D_explicit():
# set parameters
s0, strike, rfr, mat, sigma, div = 100, 100, 0.02, 1, 0.3, 0.01
Nsize, Jsize = 250, 50
# s variable setting
s_min, s_max = 0, 5 * s0
s_seq = np.linspace(s_min, s_max, Jsize + 1)
h = s_seq[1] - s_seq[0]
# time variable setting
t_min, t_max = 0, mat
t_seq = np.linspace(t_min, t_max, Nsize)
k = t_seq[1] - t_seq[0]
print('criterion is {}'.format(k / (h ** 2)))
# solution grid u setting
u = np.empty((Nsize + 1, Jsize + 1))
# initial_condition
u[0, :] = np.array([max(s - strike, 0) for s in s_seq])
# recursive formula
for n in range(Nsize):
for j in range(1, Jsize):
Sj = s_seq[j]
alpha = (-(rfr - div) * Sj / (2 * h) + (sigma * Sj / h) ** 2 / 2) * k
beta = (1 / k - (sigma * Sj / h) ** 2 - rfr) * k
gamma = ((rfr - div) * Sj / (2 * h) + (sigma * Sj / h) ** 2 / 2) * k
u[n + 1, j] = alpha * u[n, j - 1] + beta * u[n, j] + gamma * u[n, j + 1]
u[n + 1, -1] = 2 * u[n + 1, -2] - u[n + 1, -3]
u[n + 1, 0] = 2 * u[n + 1, 1] - u[n + 1, 2]
exact_value = np.array([CallOptionBS(s, strike, mat, rfr, 0, sigma) for s in s_seq[1:]])
fdm_value = np.array(u[-1, 1:])
bs = CallOptionBS(s0, strike, mat, rfr, div, sigma)
print('call price is {:.3f}'.format(bs))
jth = np.where(s_seq == s0)[0][0]
print('FDM call price is {:.3f}'.format(u[-1, jth]))
plt.figure(figsize=(20, 10))
plt.subplot(1, 2, 1)
plt.plot(s_seq[1:], exact_value, label='exact value')
plt.plot(s_seq[1:], fdm_value, label='fdm value')
plt.title('Exact vs FDM')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(s_seq[1:], fdm_value - exact_value, label='value difference(FDM-Exact)')
plt.legend()
plt.show()
if __name__ == '__main__':
Solve_BSEquation_1D_explicit()
코드를 간략히 살펴보겠습니다.
N = norm.cdf # 표준정규분포의 cdf 함수
def CallOptionBS(S, K, T, r, q, sigma): # 콜옵션의 closed form
if T == 0: # 잔존만기가 0일 때는 만기 payoff을 따로 계산한다.
return np.max(S - K, 0)
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
return S * np.exp(-q * T) * N(d1) - K * np.exp(-r * T) * N(d2)
Nsize, Jsize = 250, 50 # 잔존만기 시간축은 Nsize =250개, 주가축은 Jsize = 50개로 나눈다
# s variable setting
s_min, s_max = 0, 5 * s0 # S_max 를 현재가의 5배 정도로 충분히 크게 잡음
s_seq = np.linspace(s_min, s_max, Jsize + 1) #주가를 0에서 5S0 까지 Jsize개로 나눔.
h = s_seq[1] - s_seq[0] #주가 grid사이의 간격
# time variable setting
t_min, t_max = 0, mat
t_seq = np.linspace(t_min, t_max, Nsize) # 0과 maturity 사이를 Nsize개로 나눔
k = t_seq[1] - t_seq[0] # 시간 grid사이의 간격을 구함
print('criterion is {}'.format(k / (h ** 2))) #explicit FDM의 수렴 여부를 결정하는 값을 출력해봄○ k/h^2 의 값이 heat equation의 explicit FDM의 수렴 여부를 결정했으므로 한 번 출력해 보는 것입니다.
u = np.empty((Nsize + 1, Jsize + 1))
# 잔존만기 축은 0=t0 < t1 < ..< t_{Nsize} 로 분할되므로 배열size가 Nsize+1개
# 주가 축도 마찬가지로 Jsize+1개임 # initial_condition
# 시간 0 index에 만기 payoff 배열을 구해서 넣음
u[0, :] = np.array([max(s - strike, 0) for s in s_seq])
# recursive formula
for n in range(Nsize):
for j in range(1, Jsize):
Sj = s_seq[j] # j index에 위치한 주가의 값. 아래 alpha, beta, gamma 계수구할 때 씀
# 점화식의 계수들
alpha = (-(rfr - div) * Sj / (2 * h) + (sigma * Sj / h) ** 2 / 2) * k
beta = (1 / k - (sigma * Sj / h) ** 2 - rfr) * k
gamma = ((rfr - div) * Sj / (2 * h) + (sigma * Sj / h) ** 2 / 2) * k
# 점화식
u[n + 1, j] = alpha * u[n, j - 1] + beta * u[n, j] + gamma * u[n, j + 1]
u[n + 1, -1] = 2 * u[n + 1, -2] - u[n + 1, -3] # S_max 쪽의 경계 조건
u[n + 1, 0] = 2 * u[n + 1, 1] - u[n + 1, 2] # S=0 쪽의 경계 조건○ u[:, -1]의 -1은 마지막 index를 뜻합니다. 마찬가지로, -2, -3은 각각 마지막에서 두 번째, 세 번째를 의미합니다.
# S0 < S1 < ...< S_{Jsize} 각각에 대해서 콜옵션 exact_value와 fdm value를 구한다.
# s_seq[1:] 처럼 index 0을 뺀 이유는 closed form이 S=0을 대입하면 오류나기 때문
exact_value = np.array([CallOptionBS(s, strike, mat, rfr, 0, sigma) for s in s_seq[1:]])
fdm_value = np.array(u[-1, 1:])
bs = CallOptionBS(s0, strike, mat, rfr, div, sigma) # 콜옵션 exact solution을 구하고 출력
print('call price is {:.3f}'.format(bs))
jth = np.where(s_seq == s0)[0][0] #numpy.where 함수로 s0 가 s_seq에서 위치한 index를 찾음
print('FDM call price is {:.3f}'.format(u[-1, jth])) #해당 index의 가장 마지막 시간index의 값 출력○ exact solution과 FDM solution의 값을 비교해 보기 위해 작성했습니다.
결과를 보실까요?
criterion is 4.016064257028112e-05
call price is 12.245
FDM call price is 12.115○ Closed form으로 구한 값과 FDM의 값이 유사하게 나오죠. FDM이 제대로 작동하는 것을 볼 수 있습니다.
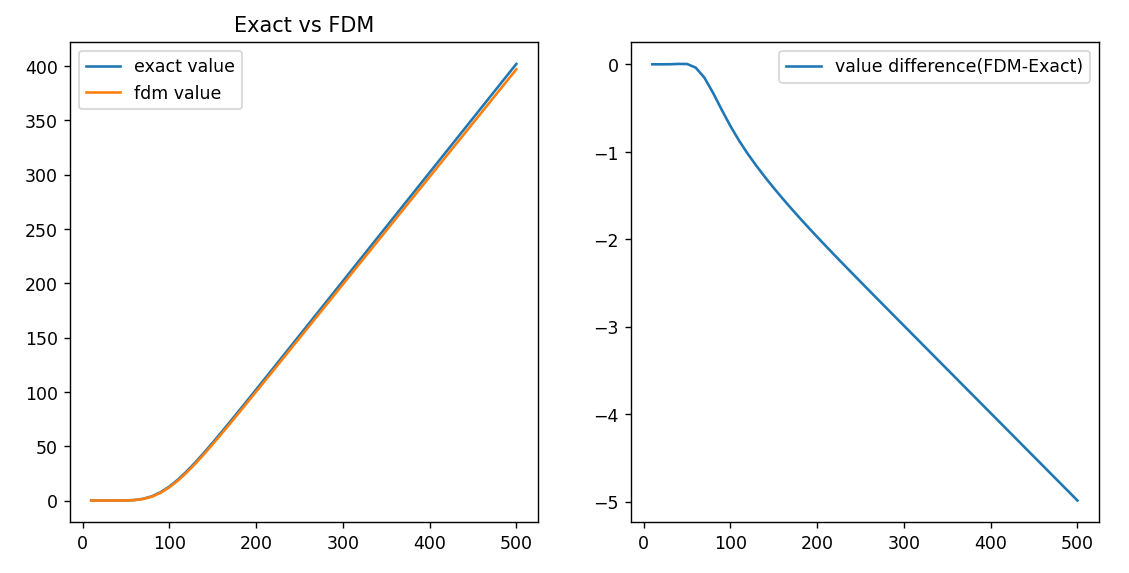
○ 왼쪽 그래프는 closed form으로 구한 그래프와 FDM으로 구한 그래프를 중첩한 것입니다. 유사합니다.
○ 둘 사이의 차이를 오른쪽에 표시해 봤습니다. 500까지 올라가면 5 정도 벌어지네요.
한계
explicit FDM은 단순한 점화식을 풀면 되는 문제라 구현이 쉽습니다만, 이것이 걸핏하면 수렴성이 깨져서 문제입니다.
Nsize, Jsize = 100, 50위의 코드에서 Nsize, Jsize를 위와 같이 바꾸면 그래프가 다음과 같이 나옵니다.
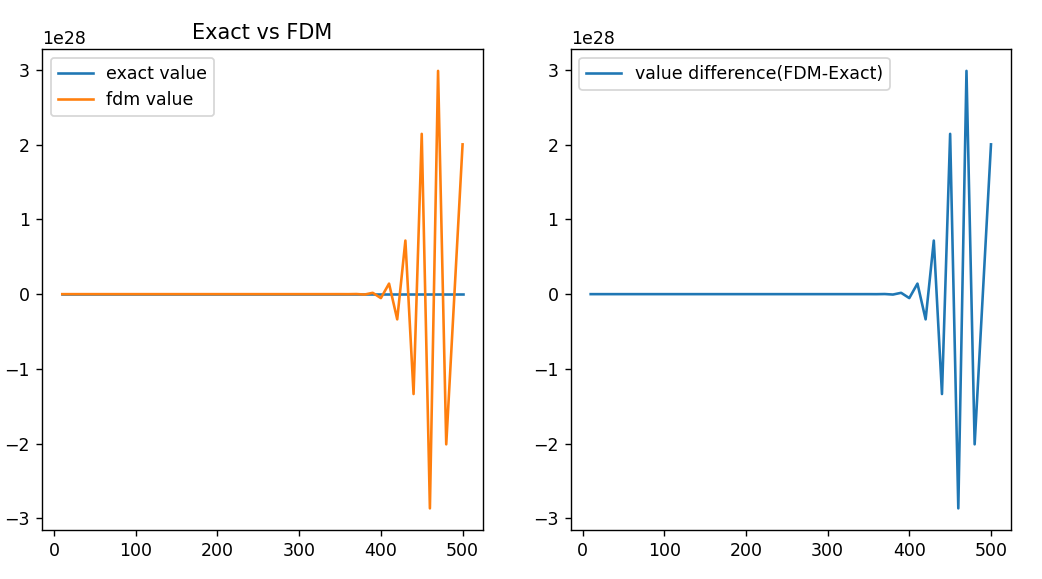
엄청나죠? 따라서 explicit FDM은 값의 안정성을 따질 때 선호하는 방법이 아닙니다.
다음 글에서는 조금 복잡하고 계산 시간이 걸리지만 값의 수렴성은 확실히 보장되는 함축적 방법(implicit method)에 대해 알아보겠습니다.
'금융공학' 카테고리의 다른 글
| 옵션 #6. 옵션 프리미엄 구하기 실습: MonteCarlo Simulation (0) | 2022.08.21 |
|---|---|
| 옵션 #5. 옵션 프리미엄 구하기 실습: 함축적 FDM (0) | 2022.08.19 |
| 옵션 #3. 옵션 프리미엄 구하기(FDM) (1) | 2022.08.18 |
| 옵션 #2. 옵션 프리미엄 구하기(Closed form) (0) | 2022.08.17 |
| 옵션 #1. 옵션이란? 옵션의 유명한 관계식이 있다던데.. (2) | 2022.08.17 |


댓글