이 글은
2022.12.20 - [분류 전체보기] - 1star 스텝다운 ELS의 계산(FDM)
1star 스텝다운 ELS의 계산(FDM)
이 글은 1star 스텝다운 ELS의 계산(시뮬레이션)과 2022.12.15 - [금융공학] - 1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지) 1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지) 이 글은 2022.12.1
sine-qua-none.tistory.com
에서 이어집니다.
지난 글에서는 1star ELS의 가격을 FDM을 통해 얻을 수 있는 방법론에 대해 알아봤습니다.
그럼 살펴본 이론을 통하여 직접 ELS의 가격을 구해보겠습니다. 사용 알고리즘은
Implicit FDM
입니다. 바로 python code를 보도록 하겠습니다. 대상 상품은 아래와 같은 구조입니다.

Python으로 코딩한 1 star 스텝다운 ELS 가격(Implicit FDM)
code의 얼개는 옵션, 배리어옵션, 디지털 옵션의 가격을 구했던 코드와 동일합니다. 하지만 얘네들은 time을 time to maturity(잔존만기)로 치환하여 시점이 0일 때부터 forward로 순차적으로 격자판을 구성했다면 ELS는 직관적인 이해를 위해 만기 시점의 조건으로부터 backward로 구해보도록 하겠습니다.
import numpy as np
import matplotlib.pyplot as plt
import time
class Market:
def __init__(self, rfr):
self._rfr = rfr
class Underlying:
def __init__(self, refprice, spotvalue, volatility, dividend):
self._volatility = volatility
self._dividend = dividend
self._spot = spotvalue
self._refprice = refprice
def OneDimELS_FDM(objUnderlying: Underlying, objMarket: Market, redemption_schedule, coupon,
full_dummy, barrier, ki_barrier, n_iteration):
vol = objUnderlying._volatility
div = objUnderlying._dividend
rfr = objMarket._rfr
current_spot = objUnderlying._spot
refprice = objUnderlying._refprice
dt = 1 / 250
maturity = redemption_schedule[-1]
start_time = time.time()
nSchedule = len(redemption_schedule)
Jsize = 1000
# s variable setting
s_min, s_max = 0, 5 * refprice
s_seq = np.linspace(s_min, s_max, Jsize + 1)
h = s_seq[1] - s_seq[0]
# time variable setting
t_min, t_max = 0, maturity
Nsize = t_max - t_min
t_seq = np.arange(t_min, t_max + 1)
k = dt
# solution grid u setting
u = np.empty((Nsize + 1, Jsize + 1))
ku = np.empty((Nsize + 1, Jsize + 1))
# initial_condition, not ki u grid
mat_payoff_noki = [
1 + coupon[-1] if s / refprice >= barrier[-1] else 1 + full_dummy if s / refprice >= ki_barrier else s for s in
s_seq]
mat_payoff_ki = [1 + coupon[-1] if s / refprice >= barrier[-1] else s / refprice for s in s_seq]
u[-1, :] = np.array(mat_payoff_noki)
ku[-1, :] = np.array(mat_payoff_ki)
# recursive formula
nth_chance = nSchedule - 2 # 마지막 조기상환 index
for n in range(Nsize + 1)[::-1]:
# 조기상환 chance
if n == redemption_schedule[nth_chance]:
u[n, :] = np.where(s_seq / refprice >= barrier[nth_chance], 1 + coupon[nth_chance], u[n, :])
ku[n, :] = np.where(s_seq / refprice >= barrier[nth_chance], 1 + coupon[nth_chance], ku[n, :])
nth_chance -= 1
# make tridiagonal matrix
diag = np.array([1 / k + (vol * x / h) ** 2 + rfr for x in s_seq[1:Jsize]])
under = np.array([(rfr - div) * x / 2 / h - 1 / 2 * (vol * x / h) ** 2 for x in s_seq[1:Jsize]])
over = np.array([-(rfr - div) * x / 2 / h - 1 / 2 * (vol * x / h) ** 2 for x in s_seq[1:Jsize]])
diag[0] = 2 * under[0] + diag[0]
over[0] = - under[0] + over[0]
diag[-1] = diag[-1] + 2 * over[-1]
under[-1] = under[-1] - over[-1]
# solve tridiagonal matrix
known, known_ki = u[n, 1: Jsize] / k, ku[n, 1: Jsize] / k
unknown, unknown_ki = thomas(under, diag, over, known), thomas(under, diag, over, known_ki)
u[n - 1, 1:Jsize] = unknown
ku[n - 1, 1:Jsize] = unknown_ki
# set boundary condition
u[n - 1, 0] = 2 * u[n - 1, 1] - u[n - 1, 2]
u[n - 1, -1] = 2 * u[n - 1, -2] - u[n - 1, -3]
ku[n - 1, 0] = 2 * ku[n - 1, 1] - ku[n - 1, 2]
ku[n - 1, -1] = 2 * ku[n - 1, -2] - ku[n - 1, -3]
u[n - 1, :] = np.where(s_seq / refprice >= ki_barrier, u[n - 1, :], ku[n - 1, :])
cal_time = round(time.time() - start_time, 3)
els_value = np.interp(current_spot, s_seq, u[0, :])
return els_value, u, cal_time, s_seq, t_seq
def thomas(a, b, c, d):
""" A is the tridiagnonal coefficient matrix and d is the RHS matrix"""
"""
a is lower diagonal a2,a3,..,a_N, meaning
b is diagonal b1,b2,b3,..,b_N meaning
c is upper diagonal c1,c2,c3,.. c_{N-1} meaning
"""
N = len(a)
cp = np.zeros(N, dtype='float64') # store tranformed c or c'
dp = np.zeros(N, dtype='float64') # store transformed d or d'
X = np.zeros(N, dtype='float64') # store unknown coefficients
# Perform Forward Sweep
# Equation 1 indexed as 0 in python
cp[0] = c[0] / b[0]
dp[0] = d[0] / b[0]
# Equation 2, ..., N (indexed 1 - N-1 in Python)
for i in np.arange(1, (N), 1):
dnum = b[i] - a[i] * cp[i - 1]
cp[i] = c[i] / dnum
dp[i] = (d[i] - a[i] * dp[i - 1]) / dnum
# Perform Back Substitution
X[(N - 1)] = dp[N - 1] # Obtain last xn
for i in np.arange((N - 2), -1, -1): # use x[i+1] to obtain x[i]
X[i] = (dp[i]) - (cp[i]) * (X[i + 1])
return (X)
code를 살펴보도록 하죠.
class Market과 class Underlying 은 1star 스텝다운 ELS의 계산(시뮬레이션)의 code 부분을 살펴보시기 바랍니다.
또,
def thomas(a, b, c, d):부분은 3중 대각행렬의 풀이의 내용을 참고하시면 됩니다. implicit FDM을 푸는데 결정적인 역할을 합니다.
남은 부분도 좀 살펴보겠습니다.
nSchedule = len(redemption_schedule) # 상환스케쥴 개수(예. 3y6m, 조기/만기상환 6개)
Jsize = 1000 # stock 의 범위를 나누는 갯수 : 1000 등분
# s variable setting
s_min, s_max = 0, 5 * refprice # s_min은 0, s_max는 기준가의 5배 : 500(기준가 100일때)
s_seq = np.linspace(s_min, s_max, Jsize + 1) # [s_min, s_max] 구간을 Jsize 등분한다.
h = s_seq[1] - s_seq[0] # s의 차분 : ds
# time variable setting
t_min, t_max = 0, maturity # 현재시점 0, 만기 T days일 때, [0,T]
Nsize = t_max - t_min # 1일 간격으로 나눈다, Nsize = t_max - t_min
t_seq = np.arange(t_min, t_max + 1) # 1일 가격으로 [0,T]를 나눔
k = dt # 1일 시점차 dt = 1/250
# solution grid u setting
u = np.empty((Nsize + 1, Jsize + 1)) # 시점은 [0,T]를 Nsize로, 주가는 [0, 5s0]를 Jsize로 나눔
ku = np.empty((Nsize + 1, Jsize + 1)) # u : 노낙인 격자판, ku: 낙인격자판
# 첫째 성분이 시점 index, 둘째 성분이 주가 index
# initial_condition, not ki u grid
mat_payoff_noki = [
1 + coupon[-1] if s / refprice >= barrier[-1] else 1 + full_dummy if s / refprice >= ki_barrier else s for s in
s_seq] # 노낙인 상태에서의 만기payoff : coupon, full-dummy, 손실 3part
mat_payoff_ki = [1 + coupon[-1] if s / refprice >= barrier[-1] else s / refprice for s in s_seq]
# 낙인 상황에서는 coupon 및 손실상환 2part
u[-1, :] = np.array(mat_payoff_noki) # u의 마지막 시점 index에 노낙인 payoff
ku[-1, :] = np.array(mat_payoff_ki) # ku의 마지막 시점 index에 낙인 payoff
nth_chance = nSchedule - 2 # 마지막 조기상환 index
# u와 ku 격자판의 조기상환 시점에 쿠폰상환 조건을 처리하기 위한 index
for n in range(Nsize + 1)[::-1]: # 시점을 만기(T)에서 현재(0)까지 거꾸로 돌리며
# 조기상환 chance
if n == redemption_schedule[nth_chance]: # 만일 조기상환 시점이라면,
u[n, :] = np.where(s_seq / refprice >= barrier[nth_chance], 1 + coupon[nth_chance], u[n, :])
# 배리어 이상인 부분의 u값은 1+coupon으로 치환
ku[n, :] = np.where(s_seq / refprice >= barrier[nth_chance], 1 + coupon[nth_chance], ku[n, :])
# 배리어 이상인 부분의 ku값은 1+coupon으로 치환
nth_chance -= 1 # 그 전 조기상환 chance index를 기억
# make tridiagonal matrix
# 시점 index (n+1)일 때에서 n일 때를 얻는 연립방정식을 풀기위해 tridiagonal marix 만듬
diag = np.array([1 / k + (vol * x / h) ** 2 + rfr for x in s_seq[1:Jsize]])
under = np.array([(rfr - div) * x / 2 / h - 1 / 2 * (vol * x / h) ** 2 for x in s_seq[1:Jsize]])
over = np.array([-(rfr - div) * x / 2 / h - 1 / 2 * (vol * x / h) ** 2 for x in s_seq[1:Jsize]])
diag[0] = 2 * under[0] + diag[0]
over[0] = - under[0] + over[0]
diag[-1] = diag[-1] + 2 * over[-1]
under[-1] = under[-1] - over[-1]
# solve tridiagonal matrix
known, known_ki = u[n, 1: Jsize] / k, ku[n, 1: Jsize] / k
unknown, unknown_ki = thomas(under, diag, over, known), thomas(under, diag, over, known_ki)
u[n - 1, 1:Jsize] = unknown #해를 풀면 그것이 시점 n일 때의 u의 값
ku[n - 1, 1:Jsize] = unknown_ki #시점 n일 때의 ku 값
# set boundary condition
# boundary condition은 u와 ku의 끝 boundary의 감마가 0이 되게끔, 즉, 선형으로..
u[n - 1, 0] = 2 * u[n - 1, 1] - u[n - 1, 2]
u[n - 1, -1] = 2 * u[n - 1, -2] - u[n - 1, -3]
ku[n - 1, 0] = 2 * ku[n - 1, 1] - ku[n - 1, 2]
ku[n - 1, -1] = 2 * ku[n - 1, -2] - ku[n - 1, -3]
# 노낙인 격자판 u와 낙인 격자판 ku의 짬뽕.
# u 격자판의 배리어 밑을 의미하는 영역을 ku로 치환하여 낙인이 반영된 값을 산출
u[n - 1, :] = np.where(s_seq / refprice >= ki_barrier, u[n - 1, :], ku[n - 1, :])
cal_time = round(time.time() - start_time, 3) #계산 완료
# 선형보간법으로 u격자판에서 시점 0, 즉 stock array: u[0,:]
# 현재가에서의 u을 보간하여 찾음
els_value = np.interp(current_spot, s_seq, u[0, :])
# u격자판, 계산소요시간, 주가 범위, 시간 범위 다 return 값으로.
return els_value, u, cal_time, s_seq, t_seq○ range(n)[::-1] 을 하면, range(n)이 뜻하는 array([0, 1,2,..., n-1])를 역순으로 표현하게 됩니다. 즉
array([n-1,...,2,1,0])
을 얻습니다.
○ numpy.interp(x, xp, fp) : xp array를 x값, fp array를 y값으로 하는 data set에서 x 값에 맞는 함숫값을 선형 보간으로 찾아내는 함수입니다.
그럼 이 함수가 잘 작동하는지 MC 값과 비교해 보도록 하겠습니다. MC 시뮬레이션 중에서도 brownian bridge를 써서 구한 결과와 비교해 볼게요. 해당 내용은 1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지)
1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지)
이 글은 2022.12.14 - [금융공학] - 1star 스텝다운 ELS의 계산(시뮬레이션) 1star 스텝다운 ELS의 계산(시뮬레이션) 이번 글부터 몇 회에 걸쳐 스텝다운 ELS의 가격을 계산하는 방법을 알아보겠습니다. 스
sine-qua-none.tistory.com
에 있습니다.
결과
def elsfdm_test():
underlying_spot = Underlying(refprice=100, spotvalue=100, volatility=0.3, dividend=0)
interest_rate = Market(0.03)
redemption_schedule = np.array([1, 2, 3, 4, 5, 6]) * 125
coupon = np.array([1, 2, 3, 4, 5, 6]) * 0.05
full_dummy = coupon[-1]
barrier = np.array([0.9, 0.9, 0.85, 0.85, 0.8, 0.8])
ki_barrier = 0.6
n_iteration = 10000
els_price_bb, cal_time_bb, prob_bb = OneDimELS_MC_BB(underlying_spot, interest_rate, redemption_schedule, coupon,
full_dummy, barrier, ki_barrier, n_iteration)
els_fdm, uu, cal_time_fdm, s_seq, t_seq = OneDimELS_FDM(underlying_spot, interest_rate, redemption_schedule, coupon,
full_dummy, barrier, ki_barrier, n_iteration)
np.set_printoptions(suppress=True)
print('ELS value(MC with BB): {:.3f}'.format(els_price_bb))
print('elapsed time : {}'.format(cal_time_bb))
print('\n')
print('ELS value(FDM) : {:.3f}'.format(els_fdm))
print('elapsed time : {}'.format(cal_time_fdm))
if __name__ == '__main__':
elsfdm_test()
그냥 결과를 찍어본 것에 불과하므로 바로 실행 결과를 보겠습니다.
ELS value(MC with BB): 0.988
elapsed time : 1.433
ELS value(FDM) : 0.984
elapsed time : 12.586가격이 대동소이합니다. 하지만 계산에 걸린 시간 측면에서 차이가 많이 나네요. 그렇다고 FDM이 안 좋다고 할 수 있을까요?
사실 FDM은 계산시간이 좀 걸리지만, 큰 장점이 있습니다.
격자판의 모든 시점, 모든 기초자산 가격에 대한 ELS값을 구해놓은 것이 바로 FDM 방법론
위의 내용이 ELS FDM 격자판이 가지고 있는 가장 훌륭한 장점입니다. 모든 시점과 모든 기초자산 가격에서 ELS 값을 계산해 놓았기 때문에 주가의 변화, 시점의 변화에 따라 번거롭게 계산할 할 필요가 없습니다.
ELS 헤지운용을 하기 위해서는 오늘의 주가가 어떻게 변할지 모르므로 장 시작 전 미리 오늘의 주가가 될 법한 값들에 대해서 모두 다 계산해 놓습니다. 이런 방대한 작업을 할 때, FDM 격자판 하나 딱 가지고 있으면 든든하겠죠.
반면에 일회성으로 한 점에서의 가격을 알고 싶을 땐 격자판 전부가 필요 없겠죠. 이 때는 시간 관계상 시뮬레이션 방법도 좋아 보입니다.
이번엔 여러 개의 주가에 대해서 MC시뮬레이션 결과와 FDM 결과를 비교해 보겠습니다.
def comparisonTest():
underlying_spot = Underlying(refprice=100, spotvalue=100, volatility=0.3, dividend=0)
interest_rate = Market(0.03)
redemption_schedule = np.array([1, 2, 3, 4, 5, 6]) * 125
coupon = np.array([1, 2, 3, 4, 5, 6]) * 0.05
full_dummy = coupon[-1]
barrier = np.array([0.9, 0.9, 0.85, 0.85, 0.8, 0.8])
ki_barrier = 0.6
n_iteration = 10000
# 주어진 ELS 상품의 FDM값 계산
els_fdm, uGrid, cal_time_fdm, s_seq, t_seq = OneDimELS_FDM(underlying_spot, interest_rate, redemption_schedule,
coupon,
full_dummy, barrier, ki_barrier, n_iteration)
mc_list = [] # 20개의 주가에 대해 MC value 값을 담을 list
fdm_list = [] # 20개의 주가에 대해 FDM value 값을 담을 list
x = [] # graph의 x 값
cal_time_mc = 0 # MC 계산시 소요되는 시간
for i in range(20):
curr_price = 50 + 5 * i # 주가: 50, 55, ..., 145
underlying_spot = Underlying(refprice=100, spotvalue=curr_price, volatility=0.3, dividend=0)
# 주어진 상품의 각 주가별 MC값 및 소요시간 계산
mc_value, ct, _ = OneDimELS_MC_BB(underlying_spot, interest_rate, redemption_schedule, coupon,
full_dummy, barrier, ki_barrier, n_iteration)
x.append(i + 1)
mc_list.append(mc_value)
fdm_list.append(np.interp(curr_price, s_seq, uGrid[0, :]))
cal_time_mc += ct
print(mc_list)
print(fdm_list)
print('Elapsed time: MC={}, FDM={}'.format(cal_time_mc, cal_time_fdm))
plt.plot(x, mc_list, c='r', marker='o', label='MC')
plt.plot(x, fdm_list, c='b', marker='x', label='FDM')
plt.xticks([1, 5, 10, 15, 20])
plt.legend()
plt.show()
if __name__ == '__main__':
comparisonTest()결과는 다음과 같습니다.
[0.5490045217106839, 0.6106271199513978, 0.6676345184139189, 0.7411959628129626, 0.7970834711310129, 0.842446685879496, 0.8890491597738915, 0.9252435731009294, 0.9541822159148884, 0.9676861034437501, 0.9882142191996907, 1.0014832641195164, 1.0113749390366513, 1.0203076049485744, 1.0222756932232806, 1.0266311132563428, 1.0301546846851408, 1.0320476071033178, 1.0327402333176465, 1.0332112981004244]
[0.5532982837296733, 0.6147854265047006, 0.6744802636479189, 0.732147461548268, 0.7854084600565022, 0.83340068267629, 0.8755250941680183, 0.9114825845147307, 0.9413023525324664, 0.9653264061545792, 0.984144108329895, 0.9984960682113615, 1.0091747393224626, 1.0169429660083826, 1.022480219543327, 1.0263562677309195, 1.0290263011884058, 1.0308398420551421, 1.0320565983164125, 1.032864313255607]
Elapsed time: MC=15.347, FDM=13.977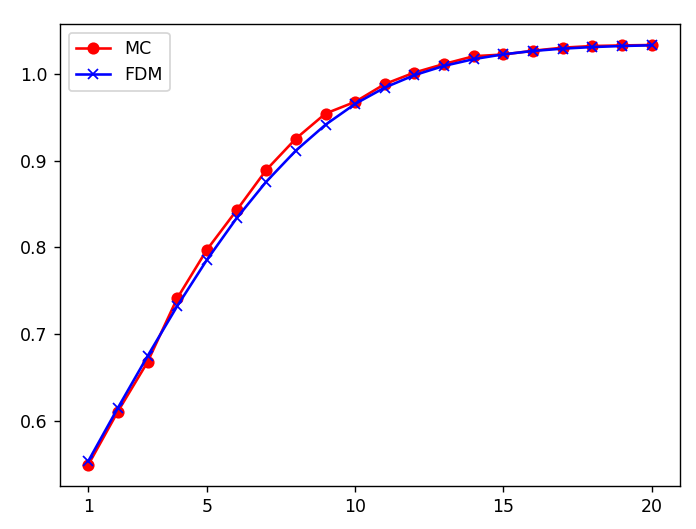
역시, 20개의 주가에 대해서 FDM은 격자 하나 구해 놓으면 다 계산이 되고, MC는 일일이 개별 계산을 해야 하죠. 따라서 여러 값을 구할 때는 FDM도 매우 유용한 방법임을 알 수 있습니다.
또한 MC는 발생된 난수와 시뮬레이션 횟수에 따라 값의 정확도가 좌우되지만, FDM은 비교적 안정적인 값을 보여줍니다. 또한, 위 그래프에서 FDM 결과와 MC결과가 매우 흡사하다는 것도 증명이 되었습니다.
'금융공학' 카테고리의 다른 글
| 1star 스텝다운 ELS의 계산(Binomial Tree) #2 (0) | 2022.12.22 |
|---|---|
| 1star 스텝다운 ELS의 계산(Binomial Tree) #1 (0) | 2022.12.21 |
| 1star 스텝다운 ELS의 계산(FDM) #1 (0) | 2022.12.20 |
| 1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지) (0) | 2022.12.15 |
| 1star 스텝다운 ELS의 계산(시뮬레이션) (0) | 2022.12.14 |




댓글