이번 글은
2022.12.20 - [금융공학] - 1star 스텝다운 ELS의 계산(FDM) #2
1star 스텝다운 ELS의 계산(FDM) #2
이 글은 2022.12.20 - [분류 전체보기] - 1star 스텝다운 ELS의 계산(FDM) 1star 스텝다운 ELS의 계산(FDM) 이 글은 1star 스텝다운 ELS의 계산(시뮬레이션)과 2022.12.15 - [금융공학] - 1star 스텝다운 ELS의 계산(시
sine-qua-none.tistory.com
에서 이어집니다.
몇 회의 글에 걸쳐 1star 스텝다운 ELS의 가격을 계산해 보고 있습니다. 지금까지 MonteCarlo Simulation, FDM 두 가지 방법으로 계산해 보았는데요,
○ MonteCarlo Simulation : 1star 스텝다운 ELS의 계산(시뮬레이션), 1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지
○ FDM : 1star 스텝다운 ELS의 계산(FDM) #1, 1star 스텝다운 ELS의 계산(FDM) #2
를 참고하시면 됩니다.
ELS 가격을 산출하는 또 다른 방법론은 없을까요? 본 블로그에서 알아본 다른 가격결정 방법들이 있습니다. 바로 Closed form, 즉 공식을 유도하여 계산하는 방법, 이항트리(binomial tree)를 이용하는 방법이 있죠.
ELS 상품은 조기상환 기회가 여러 개 있고, 낙인 여부까지 관찰을 해야 하므로 수학적인 공식을 만들기 굉장히 난해합니다.(항간에는 수학적 공식이 있다는 얘기도 들리긴 했지만, 눈으로 직접 확인해 본 바는 없습니다. 있어도 상당히 복잡하고 계산시간이 오래 걸릴 것 같은 게 개인적인 생각입니다.)
어쨌든 수학공식은 직접 유도를 하든, 아니면 이론을 찾든지 해서 성과가 있으면 소개하기로 하고요, 이 글에서는 남은 한 가지 방법
이항트리를 이용하여 스텝다운 ELS 가격 계산하기
를 해보도록 하겠습니다.
이항트리 복습
이항트리는 예전에 자세하게 다룬 바 있습니다.
2022.08.12 - [금융공학] - 파생상품의 가격 결정: binomial tree를 이용해 봅시다.
파생상품의 가격 결정: binomial tree를 이용해 봅시다.
이 글에서는 2022.08.11 - [금융공학] - Binomial Tree #3 : 이항 모델 가지치기 Binomial Tree #3 : 이항모델 가지치기 이 글은 2022.08.09 - [금융공학] - Binomial Tree #2: CRR 모델이란? Binomial Tree #2: CRR 모델이란? 이
sine-qua-none.tistory.com
에서 소개를 해 놓았으니, 참고해보시면 되겠습니다. 간단히 설명하자면,
이항 모형 만들기
먼저 한 단계 과정인 이항 모형, 즉 주가가 up 또는 down 두 가지 경우만 존재한다고 가정하고,위험 중립이 되도록
up, down 비율 u,d와 상승/하락확률 p,1−p를 찾아냅니다.

이항 모형을 이어붙여 이항트리 만들기
이항 모형이 한 단계 과정이라면, 이것을 이어 붙여 다단계 과정을 만듭니다. 이때 recombination을 위해 상승했다가 하락하면 다시 원위치 즉, ud=1이 되도록 세팅합니다. 이렇게 하여 타임노드 N개를 만들어 이어 붙이면 아래와 같은 삼각형 모양이 됩니다.

상품 가치 계산
위의 그림에서 제일 먼저 N일 때(제일 우측) 모든 노드에 대한 페이오프를 구하고, 각 노드를 확률 가중하고 할인하여 전 노드의 모든 갑을 구성합니다. 구체적으로 time step n과 stock step i에 위치한 노드의 파생상품 가치를 f(n,i)라 한다면,
f(n,i)=e−rΔt[pf(n+1,i+1)+(1−p)f(n+1,i)]
로 backward recursion formula를 풀어나가면 어느새 f(0,0)에 도착할테고, 이것이 현재시점 t=0에서의 파생상품 가치가 됩니다.
ELS 상품은 페이오프가 복잡합니다. FDM 격자판을 구성할 때도
○ 낙인 격자판, 노낙인 격자판 두 판 작성
○ 각 조기상환 시점에 맞는 time step에서는 조기상환 조건에 따라 페이오프 치환
○ 각 time step 별로 낙인 배리어를 하회한 stock level에 대해서는 노낙인 격자판의 값을 낙인 격자판의 값으로 치환
의 방법을 썼지요. 이항 트리도 마찬가지 입니다. 구체적으로 살펴보겠습니다.
ELS의 이항트리
두 개의 이항트리 준비
우선 두 개의 이항트리를 준비합니다. 하나는 낙인 상황을 가정한 이항트리, 다른 하나는 낙인 안친 상황의 이항트리입니다. 아래 그림을 참고해 보세요.

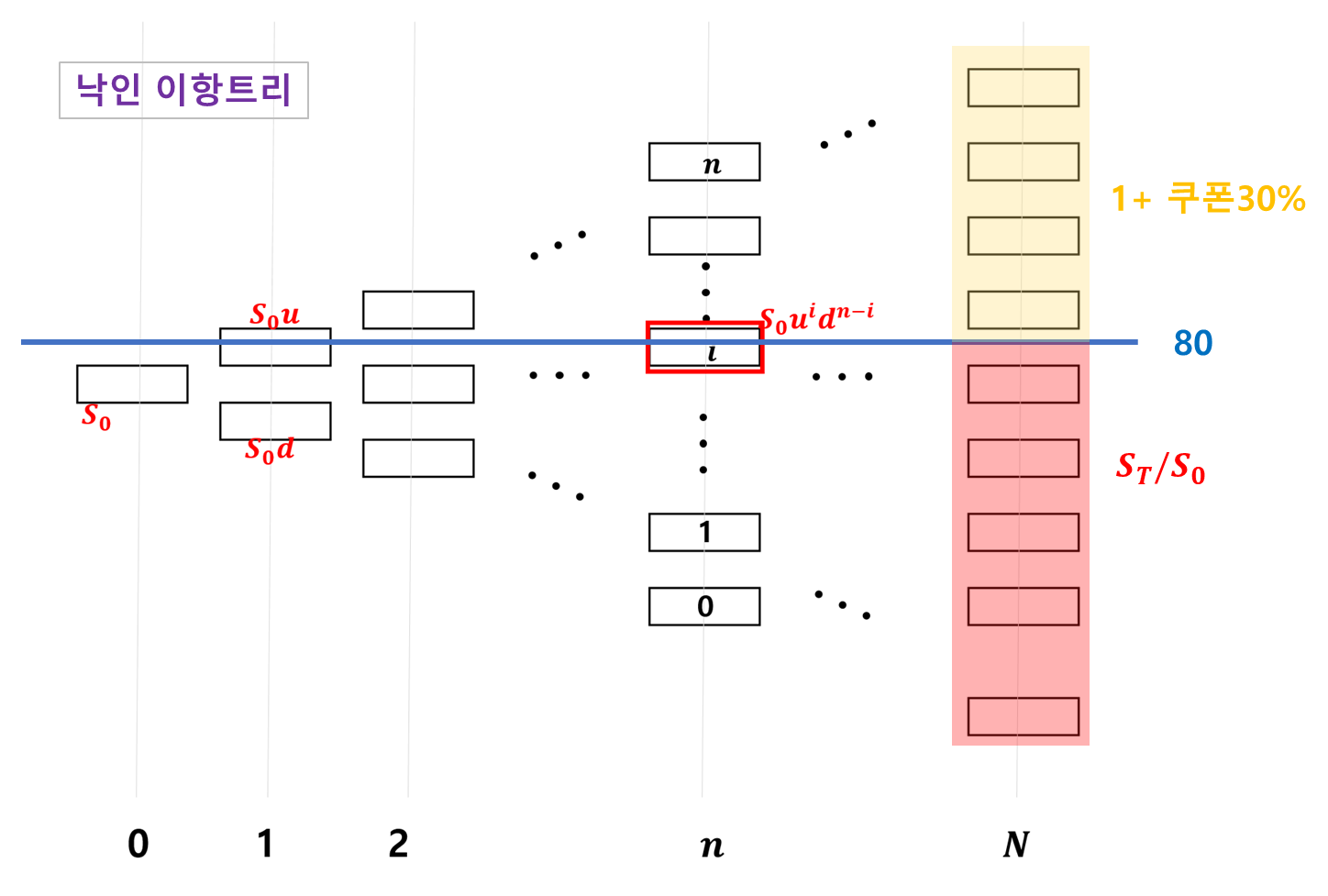
상환 시점 별 페이오프 업데이트 하기
만기시점 노드부터 backward로 오다가 5차 조기상환을 만나면 해당 배리어 이상의 stock 노드는 다 쿠폰으로 치환해 줍니다.
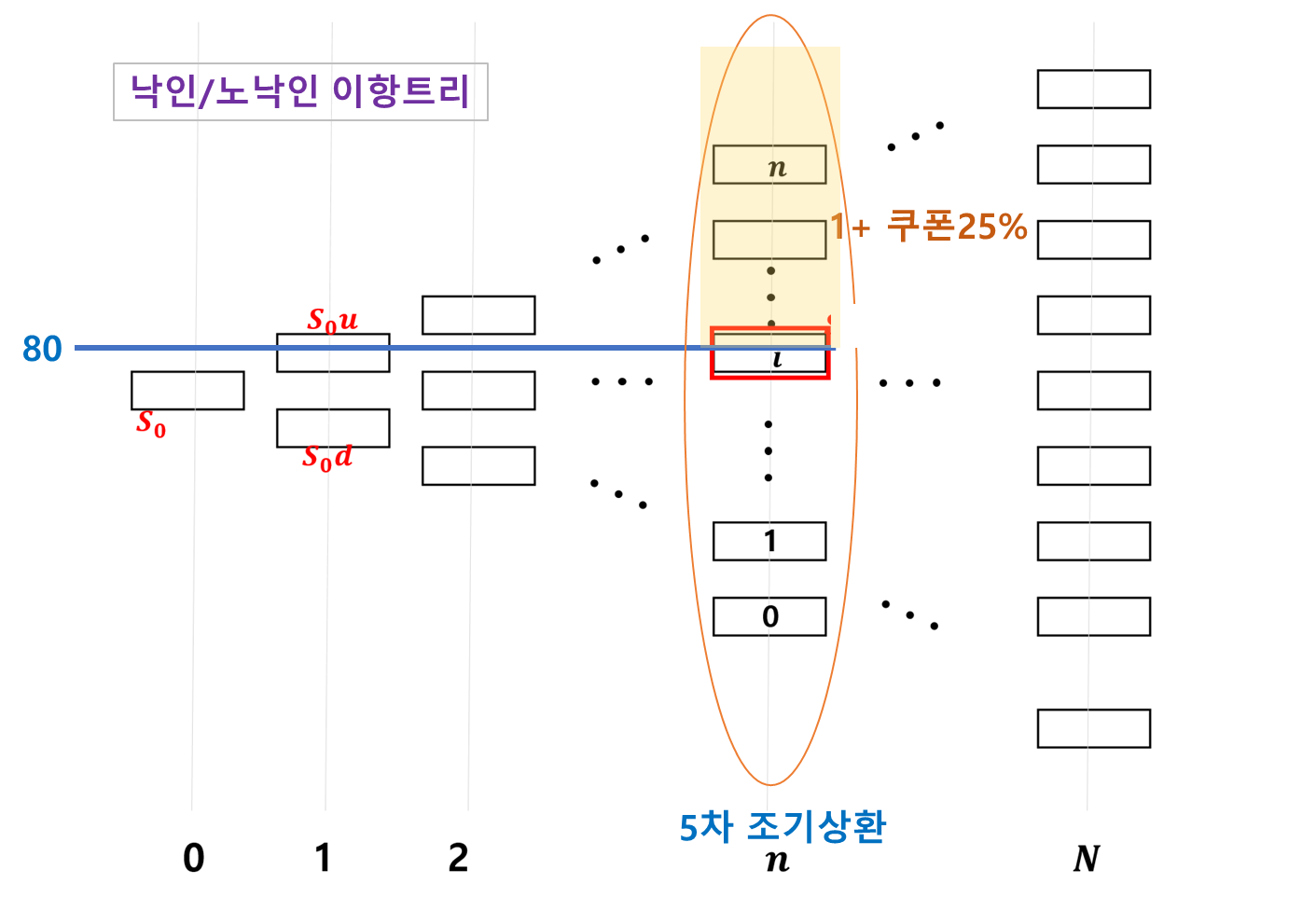
이 작업은 4차, 3차,... , 1차 조기상환 시점을 만나면 똑같은 방법으로 해줍니다.
노낙인 이항트리, 낙인 이항트리 각각에 대해 해줘야 합니다.
각 타임 노드별로 노낙인/ 낙인 이항트리 섞기
낙인 이항트리의 낙인 배리어 밑에 위치한 노드들의 값을 노낙인 이항트리에 반영해 줍니다. 그림으로 보면 아래와 같습니다.
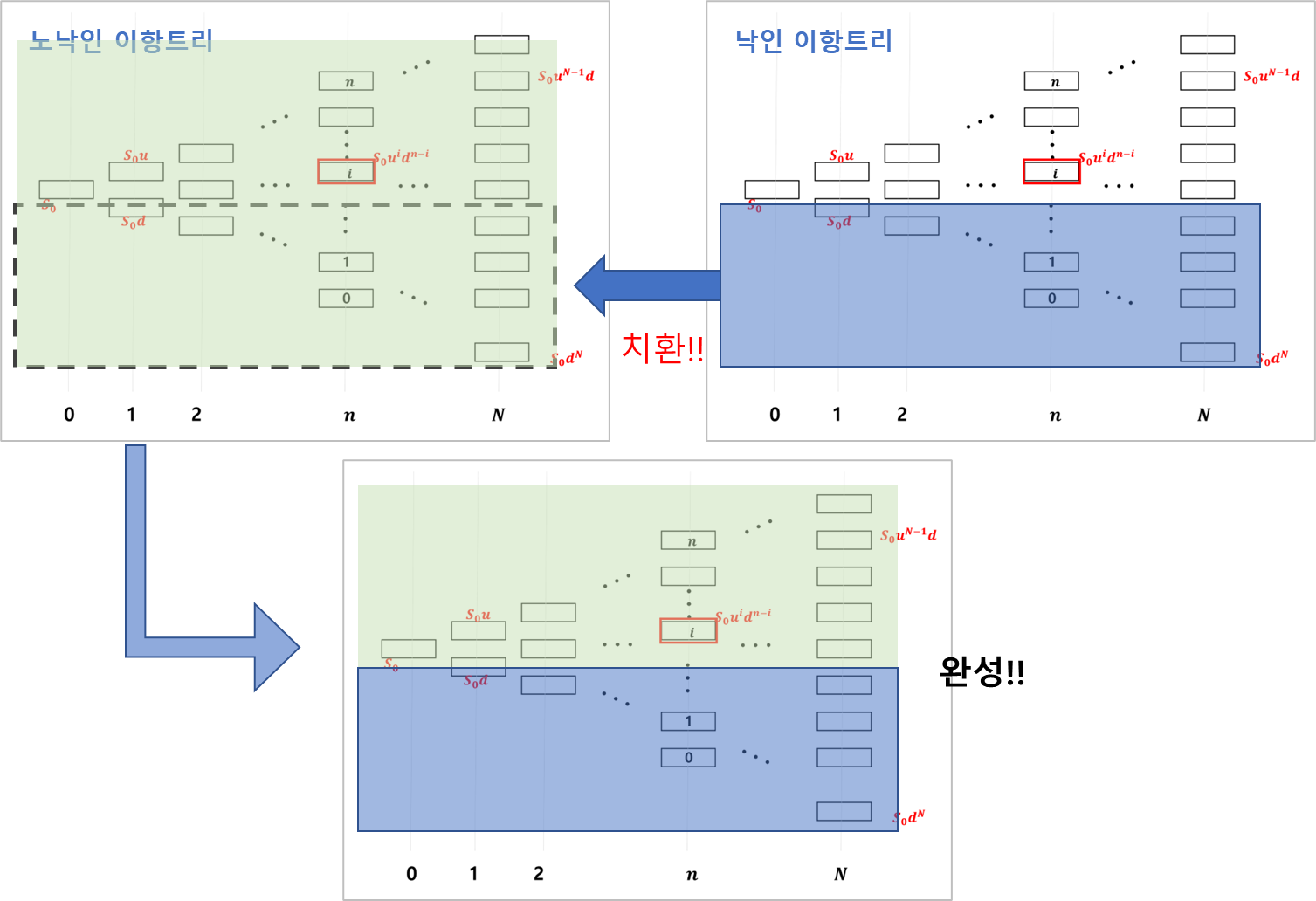
초기 노드 값 추출
위의 과정을 모두 행해 주면 모든 노드의 값이 채워지게 되고 이 중 시점 0인 노드를 선택하면 ELS의 현재가치가 됩니다.
이론을 알아보았으니, 다음 글에서 직접 coding을 통하여 ELS 가격을 구해보고 FDM 가격과 비교해 보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 옵션에도 아메리칸 스타일이 있다 (0) | 2022.12.27 |
|---|---|
| 1star 스텝다운 ELS의 계산(Binomial Tree) #2 (0) | 2022.12.22 |
| 1star 스텝다운 ELS의 계산(FDM) #2 (2) | 2022.12.20 |
| 1star 스텝다운 ELS의 계산(FDM) #1 (0) | 2022.12.20 |
| 1star 스텝다운 ELS의 계산(시뮬레이션 + 브라운브리지) (0) | 2022.12.15 |




댓글