이 글은
2022.12.14 - [금융공학] - 1star 스텝다운 ELS의 계산(시뮬레이션)
1star 스텝다운 ELS의 계산(시뮬레이션)
이번 글부터 몇 회에 걸쳐 스텝다운 ELS의 가격을 계산하는 방법을 알아보겠습니다. 스텝다운 ELS란? 스텝다운 ELS은 몇 번의 조기상환 기회를 제공하는 주가연계 상품으로써, 주가가 많이 떨어지
sine-qua-none.tistory.com
에서 이어집니다. 위 글에서는 ELS 상품의 가격을 Montecarlo Simulation으로 구해봤습니다.
대상은

이 상품이었구요.
위 상품을 구할 때 일일주가를 발생시켜 그 주가 패스에서 나오는 페이오프를 구하여 가격을 구했습니다.
하지만 일일주가패스를 만들다 보니, 한 패스를 만들 때 주가를 총 750개(250× 3년) 를 만들었습니다. 난수발생도 한 패스당 750개가 필요하죠. 만일 10,000번을 계산하면, 750만개의 난수가 필요합니다.
왜 일일주가를 모두 발생시켰나 돌이켜보면,
Knock in을 치는지 여부를 관찰하기 위해
였죠. 그런데 또 달리 생각해보면, 주가 퍼포먼스가 낙인을 쳤는지 여부와 상관없이 조기상환이나 만기상환 시점에 해당 배리어 위에만 올라와있으면 상환이 된다는 것이죠. 저번 글의 결과를 보면,
0.9833693017422173 # ELS의 가격
44.893 # 계산소요시간(sec)
[0.6798 0.0886 0.0557 0.0237 0.0231 0.0131 0.0016 0.1144] # 상환별 확률
# 1차 2차 3차 4차 5차 6차 fulldummy 손실상환1차~ 6차 쿠폰으로 상환될 확률을 더해보면 거의 90%에 육박합니다. 이 말인 즉슨, 거의 대부분이 수익 상환이 되고, 막판에 full dummy를 주느냐 아니면 손실상환이 되느냐를 결정할 때만 즉 11% 정도의 확률에만 낙인 쳤는지 여부가 중요하다는 이야기겠죠.
요지는 낙인 여부를 판단하기 위해 일일주가 패스를 모두 생성하는 것은 너무 과하다라는 것입니다.
따라서 6번의 상환시점에만 우선 주가를 생성해 보는 겁니다. 만일 6번 중 한번의 기회에서라도 상환했으면 그냥 페이오프가 결정되는 거죠. 만일 1차 조기상환 기회 때 상환이 되면, 랜덤변수 750를 발생시키던 일일주가 패스 에서 랜덤변수 1개 발생으로 확 줄게 되는 것이죠.
여러 경우를 볼까요?
1차 조기상환기회에서 끝나는 경우

우선 빨간 점들만 발생시킵니다. 빨간 점들의 위치는 조기/만기 상환시점입니다. 첫번째 빨간점이 배리어 위에 위치하므로 회색 영역의 주가 패스는 생성할 필요도 없지요. 오로지 딱 하나의 빨간점 주가만 생성하면 되는 경우입니다.
6차 상환(만기상환)으로 끝나는 경우

굳이 일일주가를 모두 생성하지 않더라도, 빨간 점 6개만 생성하여 배리어와 비교해 보면 됩니다.
이 경우는 조기상환(앞의 개 빨간 점) 기회는 지나갔으나 마지막에 폭등하여 된 경우네요. 중간에 낙인도 쳤지만 이건 중요한게 아닙니다. 바로 6번째 빨간점에서 상환됐으니까요.
이 경우에는 6개의 난수만 발생시키면 됩니다.
낙인 배리어 보다 위에서 끝났으나 낙인을 쳤는지 여부에 따라 full dummy 또는 손실상환인 경우
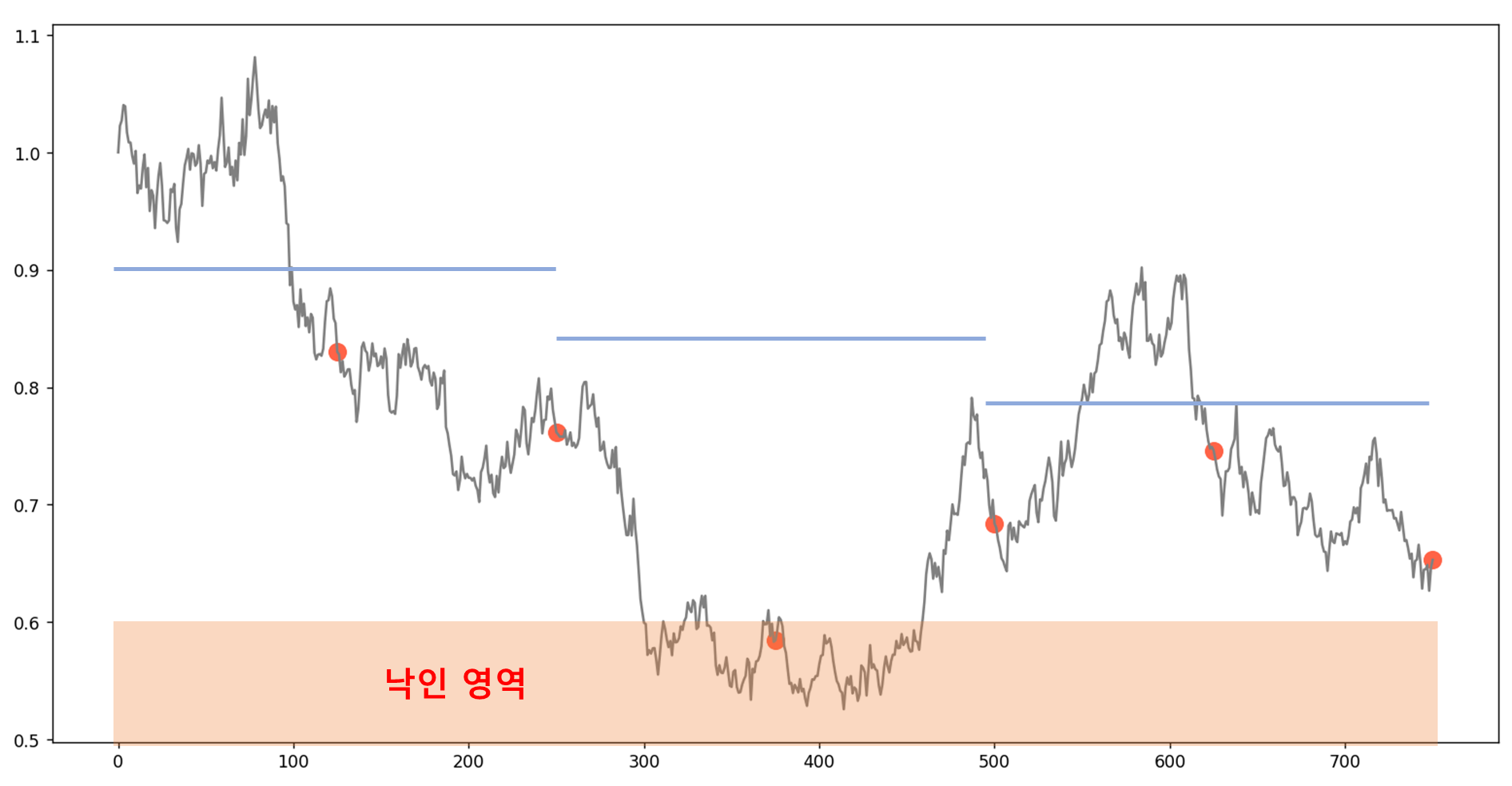
우선 빨간 점 6개를 생성해 보았더니, 조기상환은 한번도 안되고, 마지막 종가가 낙인배리어(60)과 마지막 배리어(80)사이입니다. 이 때는 낙인을 쳤는지 여부가 중요하죠. 낙인을 안친 경우라면 full dummy 쿠폰을 지급하고, 아니면 손실 상환이기 때문이죠.
그럼 빨간 점 6개가 있는 상황에서 어떻게 낙인 여부를 판단할 수 있을까요? 바로
브라운 브리지(Brownian Bridge)
를 사용하여 연결하면 됩니다. 양 끝점이 정해져 있는 상황에서 이 끝점을 연결하는 패스는 브라운 브리지 기법으로 구현 가능합니다. Brownian bridge: 1년뒤 주가타겟을 정조준하는 일일주가의 움직임을 모델링하자 #1에 관련 내용을 설명하였고, 브라운 브리지를 이용해 상품 가격을 구하는 예제는
2022.11.28 - [금융공학] - Brownian Bridge를 이용한 금융상품의 계산
Brownian Bridge를 이용한 금융상품의 계산
이번 글에서는 Brownian Bridge를 사용하여 파생상품의 평가를 어떻게 할 수 있는지 한번 알아보겠습니다. 다음과 같은 가상의 옵션상품을 설정합니다. 우선 기초자산은 어떤 지수나 주식의 퍼포먼
sine-qua-none.tistory.com
에서 설명한 바 있습니다.
이제 코딩을 해보겠습니다.
Python으로 코딩한 1 star 스텝다운 ELS 가격(Brownian Bridge 사용)
브라운 브리지를 사용하여 ELS가격을 구해보겠습니다. 코드 형식은 저번 글과 비슷합니다. Underlying class와 Market class를 도입해서 코딩했습니다.
import numpy as np
import time
class Market:
def __init__(self, rfr):
self._rfr = rfr
class Underlying:
def __init__(self, refprice, spotvalue, volatility, dividend):
self._volatility = volatility
self._dividend = dividend
self._spot = spotvalue
self._refprice = refprice
def OneDimELS_MC_BB(objUnderlying: Underlying, objMarket: Market, redemption_schedule, coupon,
full_dummy, barrier, ki_barrier, n_iteration):
vol = objUnderlying._volatility
div = objUnderlying._dividend
rfr = objMarket._rfr
current_spot = objUnderlying._spot
refprice = objUnderlying._refprice
dt = 1 / 250
drift = (rfr - div - 0.5 * vol ** 2)
maturity = redemption_schedule[-1]
sum_price = 0
temp_price = 0
nSchedule = len(redemption_schedule)
tenor = np.zeros(nSchedule)
tenor[0] = redemption_schedule[0]
tenor[1:] = np.diff(redemption_schedule)
tenor /= 250
redemp_prob = np.zeros(nSchedule + 2)
np.random.seed(0)
sum_payoff = 0
start_time = time.time()
for i in range(n_iteration):
rn = []
redem_spot = []
old_spot = current_spot
ki_occurs = False
redem_spot.append(old_spot)
for j in range(nSchedule):
rn_normal = np.random.normal()
new_spot = old_spot * np.exp(drift * tenor[j] + vol * np.sqrt(tenor[j]) * rn_normal)
if new_spot / refprice >= barrier[j]:
payoff = 1 + coupon[j]
df = np.exp(-rfr * redemption_schedule[j] / 250)
redemp_prob[j] += 1
break
else:
old_spot = new_spot
redem_spot.append(new_spot)
if new_spot / refprice < ki_barrier:
ki_occurs = True
rn.append(rn_normal)
if j == nSchedule - 1:
df = np.exp(-rfr * redemption_schedule[j] / 250)
if ki_occurs:
payoff = old_spot / refprice
redemp_prob[-1] += 1
else:
for k in range(nSchedule):
if k == 0:
t1, t2 = 0, redemption_schedule[k]
s1, s2 = redem_spot[k], redem_spot[k + 1]
zt1, zt2 = 0, (np.log(s2 / refprice) - drift * np.sqrt(t2)) / (vol * np.sqrt(t2))
else:
t1, t2 = redemption_schedule[k - 1], redemption_schedule[k]
zt1 = (np.log(s1 / refprice) - drift * np.sqrt(t1)) / (vol * np.sqrt(t1))
zt2 = (np.log(s2 / refprice) - drift * np.sqrt(t2)) / (vol * np.sqrt(t2))
wiener = np.zeros(t2 - t1 + 1)
timegrid = np.arange(t2 - t1 + 1)
for c in range(t2 - t1):
wiener[c + 1] = wiener[c] + np.random.normal() * np.sqrt(1 / 250)
bbridge = zt1 + timegrid / (t2 - t1) * (zt2 - zt1) + wiener - timegrid / (t2 - t1) * wiener[
-1]
svec = s1 * np.exp(drift * dt + vol * np.sqrt(dt) * bbridge)
if min(svec) / refprice < ki_barrier:
ki_occurs = True
break
if ki_occurs:
payoff = old_spot / refprice
redemp_prob[-1] += 1
else:
payoff = 1 + full_dummy
redemp_prob[-2] += 1
sum_payoff += df * payoff
cal_time = round(time.time() - start_time, 3)
els_value = sum_payoff / n_iteration
redemp_prob /= n_iteration
return els_value, cal_time, redemp_prob
간략히 살펴보도록 하겠습니다. 저번 글에서 설명한 부분들은 넘어갑니다.
nSchedule = len(redemption_schedule) # nSchedule : 상환스케쥴 개수 (6개)
tenor = np.zeros(nSchedule) # tenor는 다음상환시점까지의 잔존시간
tenor[0] = redemption_schedule[0] # 현재시점은 0이므로 처음 조기상환시점 T1까지 잔존시간 T1
tenor[1:] = np.diff(redemption_schedule) # T_{i-1}과 T_i 사이의 잔존시간은 T_i - T_{i-1}
tenor /= 250 # redemption_schedule의 day개념이므로 연으로 환산
redemp_prob = np.zeros(nSchedule + 2) # 각 쿠폰상환 확률(1~6) 및 fulldummy, 손실상환 확률 array○ 상환시점이 $T_1, T_2, \cdots, T_N$일 때, $T_1, T_2-T_1, T_3-T_2,\cdots T_N-T_{N-1}$을 계산합니다 그러기 위해서 numpy.diff 함수를 사용했습니다.
for i in range(n_iteration): # 시뮬레이션을 n_iteration회 돌린다.
rn = [] # 각 조기/만기상한 시점의 주가를 생성해 낸 random 변수를 저장할 list
redem_spot = [] # 각 조기/만기상한 시점의 주가를 저장할 list
old_spot = current_spot # 현재가를 old_spot 변수에 저장
ki_occurs = False # ki_occurs는 boolean type으로 낙인이 일어났는지 여부
redem_spot.append(old_spot) # redem_spot에 현재가를 우선 저장
for j in range(nSchedule): # Schedule 개수만큼 for문을 돌리며
rn_normal = np.random.normal() # 정규분포 난수 한개 발생시킴
new_spot = old_spot * np.exp(drift * tenor[j] + vol * np.sqrt(tenor[j]) * rn_normal)
# 재귀적으로 새로운 주가 생성
# 재귀적 산출을 위해 {T_i -T_{i-1}} 를 구한 것
if new_spot / refprice >= barrier[j]: # next 상환시점 주가 퍼포먼스가 배리어를 상회하면
payoff = 1 + coupon[j] # 원금 및 쿠폰지급
df = np.exp(-rfr * redemption_schedule[j] / 250)
# 할인팩터
redemp_prob[j] += 1 # 그 상환시점을 counting하여 확률구할때 씀
break # 상환신호 떴으므로 상품 종료
else:
old_spot = new_spot # 쿠폰 상환이 안된 상태(break 가 안먹음)
redem_spot.append(new_spot) # 상환시점의 주가들을 모아놓은 list
if new_spot / refprice < ki_barrier:
# 만일 상환시점 주가가 ki barrier 밑이면
ki_occurs = True # ki flag를 true로 설정
rn.append(rn_normal)
if j == nSchedule - 1: # 만기 시점일 때,
df = np.exp(-rfr * redemption_schedule[j] / 250)
# 할인팩터 구함
if ki_occurs: # ki flag 가 true이면,
payoff = old_spot / refprice
# 주가 퍼포먼스에 연동된 payoff 지급
redemp_prob[-1] += 1 # 손실상환 counting은 redemp_prob 제일 마지막 원소에
else: # ki flag가 false이면,
# 즉 상환시점의 주가상태는 ki 친 상황이 아니면
# 상환시점 사이에서 knock in을 쳤는지 알아봐야 한다!
for k in range(nSchedule):
# Brownian Bridge를 만들기 위해, 두 시점과 두 시점의 normal random
# 변수를 구함
if k == 0:
t1, t2 = 0, redemption_schedule[k]
s1, s2 = redem_spot[k], redem_spot[k + 1]
zt1, zt2 = 0, (np.log(s2 / refprice) - drift * np.sqrt(t2)) / (vol * np.sqrt(t2))
else:
t1, t2 = redemption_schedule[k - 1], redemption_schedule[k]
zt1 = (np.log(s1 / refprice) - drift * np.sqrt(t1)) / (vol * np.sqrt(t1))
zt2 = (np.log(s2 / refprice) - drift * np.sqrt(t2)) / (vol * np.sqrt(t2))
wiener = np.zeros(t2 - t1 + 1)
timegrid = np.arange(t2 - t1 + 1)
for c in range(t2 - t1): # 두 점을 연결하기 위한 wiener process설계
wiener[c + 1] = wiener[c] + np.random.normal() * np.sqrt(1 / 250)
bbridge = zt1 + timegrid / (t2 - t1) * (zt2 - zt1) + wiener - timegrid / (t2 - t1) * wiener[
-1] # Brownian bridge 건설
svec = s1 * np.exp(drift * dt + vol * np.sqrt(dt) * bbridge)
# Brownian bridge로 일일주가 생성
if min(svec) / refprice < ki_barrier: # 생성된 주가패스의 최저값이 ki barrier 아래면
ki_occurs = True # 낙인 flag = True
break # 이미 낙인 상황이므로 더 볼 필요도 없음
if ki_occurs:
payoff = old_spot / refprice # 낙인쳤으면 손실상환
redemp_prob[-1] += 1 # 낙인상황 counting
else:
payoff = 1 + full_dummy # 낙인안쳤으면 full dummy 상환
redemp_prob[-2] += 1 # full dummy 지급상황 counting
sum_payoff += df * payoff # 할인 페이오프 누적
결과를 보도록 하겠습니다.
python coding 결과
underlying_spot = Underlying(refprice=100, spotvalue=100, volatility=0.3, dividend=0)
# 기준가 100, 현재가격 100, 변동성 30%, 배당 0인 기초자산 객체 설계
interest_rate = Market(0.03)
# 이자율이 3%인 시장 파라미터 클래스 설계
redemption_schedule = np.array([1, 2, 3, 4, 5, 6]) * 125 #3y 6m, 6 Chance Stepdown ELS
coupon = np.array([1, 2, 3, 4, 5, 6]) * 0.05 # coupon : 10% p.a.
full_dummy = coupon[-1] # full dummy cpn = 30%
barrier = np.array([0.9, 0.9, 0.85, 0.85, 0.8, 0.8]) # 조기/만기상환 배리어
ki_barrier = 0.6 # knock in barrier
n_iteration = 10000 # simulation 횟수
els_price, cal_time, prob = OneDimELS_MC(underlying_spot, interest_rate, redemption_schedule, coupon,
full_dummy, barrier, ki_barrier, n_iteration)
els_price_bb, cal_time_bb, prob_bb = OneDimELS_MC_BB(underlying_spot, interest_rate, redemption_schedule, coupon,
full_dummy, barrier, ki_barrier, n_iteration)
np.set_printoptions(suppress=True)
print(els_price)
print(cal_time)
print(prob)
print('----------')
print(els_price_bb)
print(cal_time_bb)
print(prob_bb)
저번 글에서 코딩한 함수와, 이번 글의 코딩 함수를 같이 실행시켜 보면,
0.9833693017422173
44.893
[0.6798 0.0886 0.0557 0.0237 0.0231 0.0131 0.0016 0.1144]
----------
0.9882142191996907
0.685
[0.6796 0.0905 0.0514 0.0225 0.0242 0.0137 0.0118 0.1063]가격은 각각 98.3과 98.8 로 시뮬레이션 횟수에 비해 오차가 작게 나왔습니다. 코딩이 오류 없이 잘 되었다는 것을 알 수 있구요. 각각의 상환 확률도 대동소이합니다.
반면에 계산시간을 보실까요? 똑같은 컴퓨터 사양으로,
○ 일일이 데일리 주가패스를 생성한 경우는 45초
○ 상환시점만 주가를 생성하고, 꼭 필요한 경우에만 브라운 브리지를 연결하여 낙인여부를 체크하는 방법: 0.7초
실로 엄청난 차이가 납니다. 그만큼 쓸데 없는 난수발생을 하지 않았기 때문이죠.
브라운브리지를 적극 활용하는 것이 코딩은 좀 난해하더라도, 효율면에서는 굉장한 우위를 보여줍니다.
ELS 계산의 다른 방법이 있는가?
구조가 복잡한 ELS 상품이지만, 이 친구를 FDM(Finite Difference Method)을 통해서도 구할 수 있습니다. 다음 글에서 알아보기로 하죠.
'금융공학' 카테고리의 다른 글
| 1star 스텝다운 ELS의 계산(FDM) #2 (2) | 2022.12.20 |
|---|---|
| 1star 스텝다운 ELS의 계산(FDM) #1 (0) | 2022.12.20 |
| 1star 스텝다운 ELS의 계산(시뮬레이션) (0) | 2022.12.14 |
| 기초자산 변동성: EWMA 변동성#1 (0) | 2022.12.06 |
| 기초자산 변동성: 역사적 변동성#2 (0) | 2022.12.01 |



댓글