예전부터 부모님으로부터 이런 말씀을 많이 듣고 자랐습니다.
쓸데없이 주식같은 도박하지 말고 돈생기면 차곡차곡 은행에 넣어라. 넣다보면 어느새 2배, 3배되어 있어!
예전 광고 자료를 보실까요?

말그대로 은행에 돈을 넣어놓기만 해도 돈복사가 되는 시절이었습니다. 지금으로부터 한 50여년 전이네요. 아주 오래전 잘라 읍니다 맞춤법이 이색적입니다.
아버지께서 한일은행을 오래 다니신터라, 더 정겹네요. 약주값만 아끼셔서 본인은행에 차곡차곡 모으셨더라도 저희 집은 더욱 큰 부자가 되었겠지만, 그렇게라도 타지에서 고된 업무의 스트레스를 날려버리시고 유복한 가정을 만드시느라 고생하신 것은 저로서는 감히 아직 따라갈 수 조차 없는 희생이 아닐까 생각합니다.
아무튼 오늘은 어머니께서 입에 달고 사신,
돈 다 은행에 집어넣으면 금방 두,세배 되더라. 주식같은 거 하지 마라
를 수학적으로 고찰해 보고자 합니다.
이자, 특히 복리이자 관련하여 72법칙이라는 계산법이 있습니다. 복리로 계산할 때,
원금을 2배로 만드는데 걸리는 시간(년)과 연이자율(%) 사이의 관계식을 나타내줍니다.
걸리는 시간을 $T$, 연이자율(%)을 $r$ 이라 하면
$$ r\times T = 72$$
라는 등식을 얼추 만족시킨다라는 것입니다.
위 사진속의 금리 30%, 25.2$ 시절에는 72법칙을 이용해보면 각각
- 한일은행 30% : 원금2배에 걸리는 시간 72/30 =2.4년 = 약 2년 5개월
- 한국신탁 25.2% : 원금 2배에 걸리는 시간 72/25.2 = 2.86년 = 약 2년 10개월
입니다. 3년도 안돼 원금을 더블만드는 최강의 금리였죠. (갑자기 3년 비자발적 투자로 묶여 손실을 기록중인 저의 주식종목 하나가 생각나네요..)
요즘 예금금리는 어떨까요? 구굴에 예금금리를 검색하여 최상단에 뜨는 **은행의 슈퍼우대금리를 캡쳐해봤습니다.

도표에서 보이는 숫자중 가장 큰 1.95% 라 가정해볼까요?
- **은행 1.95% : 원금이 2배에 걸리는 시간 72/1.95 = 37.9년 =약 37년 11개월
이런, 지금 제 아들이 용돈을 예금하면 제 나이가 되어서야 2배됐다고 신나할 것 같은 시간이로군요.
자, 그럼 묻고 더블로 가! 라 주장할 수 있는 72법칙은 어떻게 유도가 된 식일까요?

이자율이 $r$(%)이고 원금이 2배 될 때 까지 걸리는 시간(년)을 $T$라 하면
$$ 2 =1\cdot (1+r/100)^T $$
가 성립합니다. 편의상 원금을 $1$로 가정했습니다.
양변에 로그를 취하면
$$ \ln(2) = T\cdot\ln(1+r/100)\tag{1}$$
입니다.
테일러 전개 내용을 보시면 식 (5)에 의해, 임의의 $|x|<1$에 대해서
$$ \ln(1+x) = x- \frac{x^2}2 + \frac{x^3}3 -\cdots $$
를 만족합니다. 그런데 이자율 같이 작은 숫자에 대해서는
$$ \ln(1+x) \approx x $$
로 근사할 수 있겠죠.
따라서, 수식(1)을 좀더 발전시키면
$$ \ln(2) = T\cdot\ln(1+r/100) = T \cdot \frac{r}{100}$$
을 만족합니다. 즉,
$$ rT = \ln 2\cdot 100 = 0.693147 \times 100 = 69.31$$
을 얻게 됩니다.
그럼 69.31의 법칙이라 하지 않고 왜 72의 법칙이라 불렀을까요? 이는 계산의 편의성에 있습니다. 72는 많은 약수로 나누어 떨어지는 수이죠. 1,2,3,4,6,8,9,.... 따라서 이자율이 이런 숫자들일 때, 금방! 암산으로~! 답을 쉽게 얻게 되는 것입니다.
(암산을 잘 하는 혹자들은 69의 법칙, 70의 법칙이라고 한다합니다.)
결론적으로 근사치지만 암산을 쉽게 하기 위해 $rT = 72$라는 식을 사용하는 것입니다. 정작 요새처럼 이자율이 낮은 상황에서 2배가 되는 시간이 37년이던, 38년이던 중요한 건 아니겠죠. 그 만큼 긴 시간이 필요하구나, 하는 감이 중요하니까요.
72법칙을 보면 연이자 $r$과 더블 걸리는 시간 $T$가 반비례 하네요. 반비례상수는 72구요. 혹시 이것을 엑셀로 추세선으로 설명해 볼 수 있을까요? 다음의 표는 연이율에 따라서 원금이 2배가 되는 기간을 정확히 구해 본 것입니다.

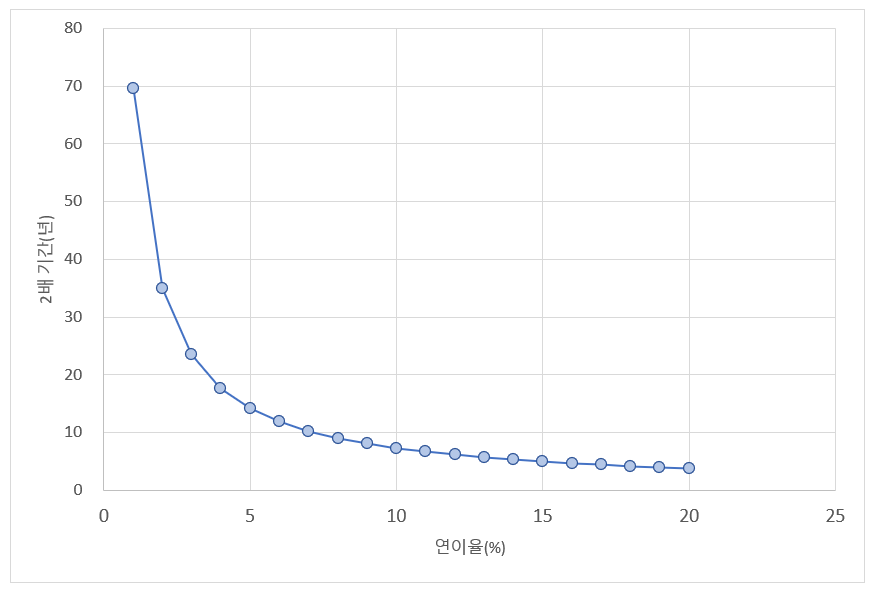
분산차트를 그려보면 위와 같습니다. 이제 추세선을 그려볼텐데, 72법칙이 $r$과 $T$가 반비례 함을 의미하므로
거듭제곱 추세선을 그려볼 예정입니다. 거듭제곱 추세선(여기를 참조)을 이용하면
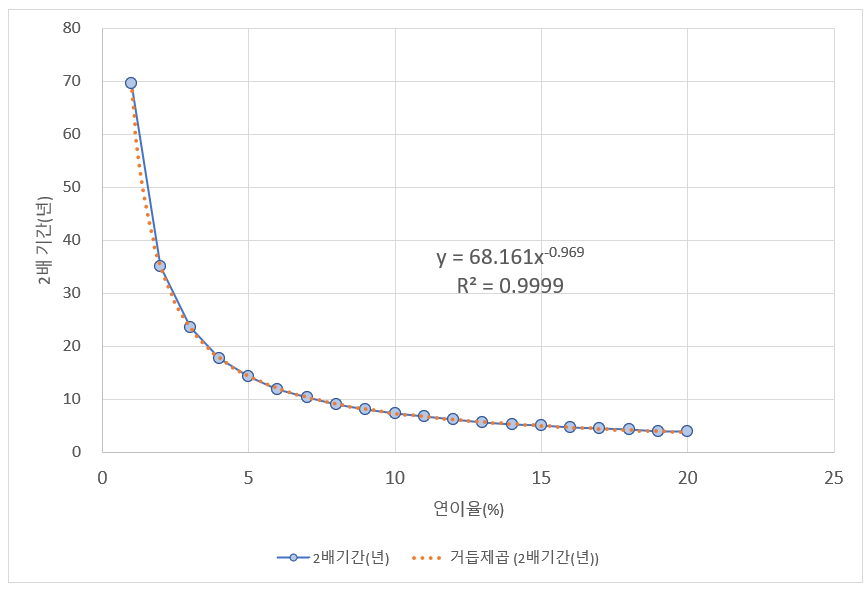
추세선의 식을 보시죠. -0,969를 거의 -1이라 생각하면 $x$(이자율)과 $y$(기간)이 반비례하고, 그 상수가 68.161이라는 뜻입니다. 즉 68의 법칙이라 불러도 될 것 같습니다.
그럼 여담으로, 72의 법칙과 68의 법칙중 어떤것이 더 정확할까요?
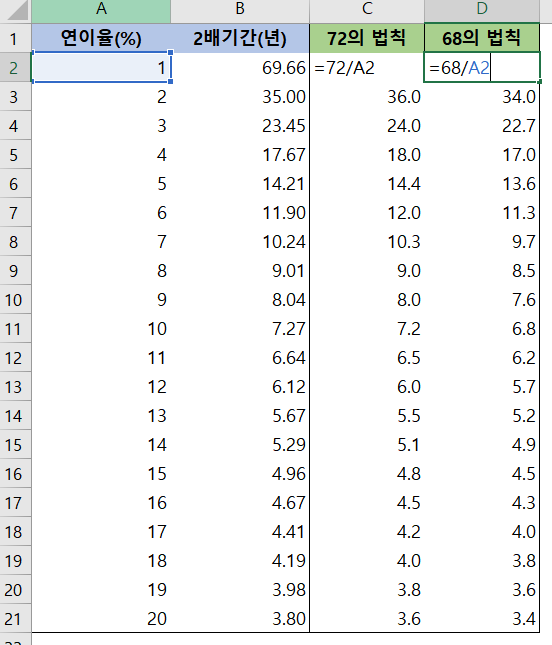
위는 72의 법칙, 68의 법칙을 사용하여 시간을 각각 C열, D열에 계산한 결과입니다. 어떤 데이터 예측이 더 좋은지는 트렌드직선 분석(여기를 참조)에서 언급한 바 있습니다. 즉 $n$개의 실제값 $\{y_i\}$와 관측값 $\{p_i\}$가 있을 때
$$ \sum_{i=1}^n (y_i-p_i)^2 \tag{2}$$
을 더 적게 하는 것이 좀 더 정확한 추정이라고 했습니다. 이제 엑셀의 SUMXMY2 함수(여기를 참조)를 사용하여 식 (2)의 결과를 각각 구해보면
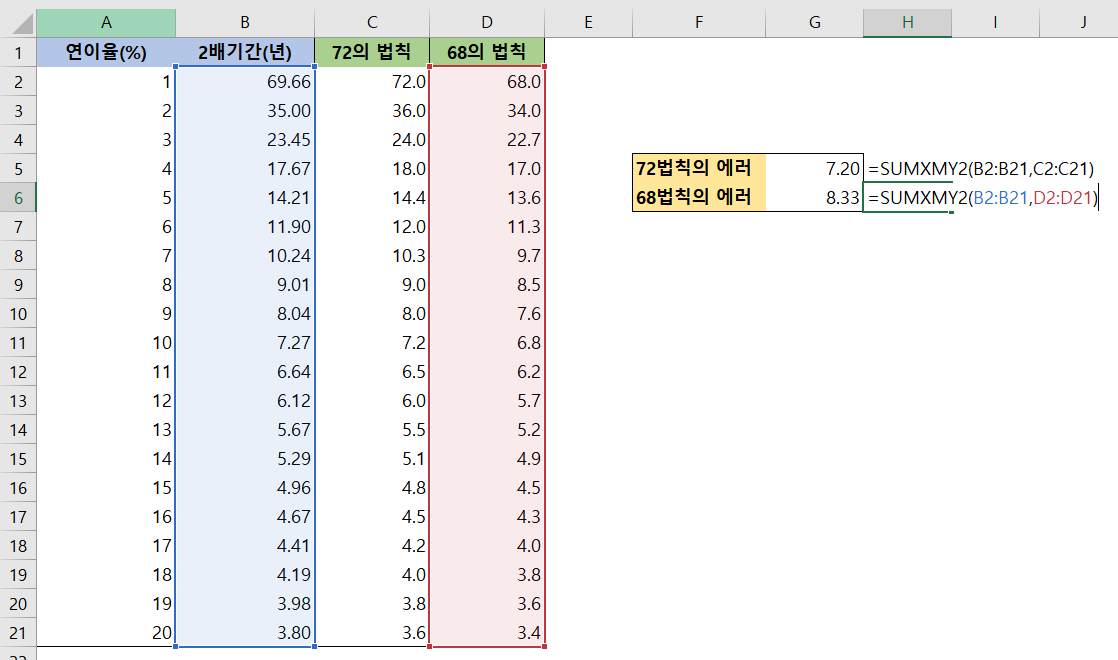
위 그림과 같이 되어, 아무래도 72법칙이 더 에러가 작습니다. 계산도 쉽구요.
72법칙에 관한 가장 오래전 기록은 15세기를 살았던 위대한 회계학자이나 수학자였던 파치올리의 저서에서 발견된 기록이라던데, 이 방법을 어떻게 알았을까요? 지금이야 $ln(2)$같은 값을 계산할 수 있으니 바로 알수 있다하더라도, 로그 발명자는 16세기 사람(존네이피어)이고 테일러 전개는 18세기 초에야 나왔는데..
돈에 관련한 직관의 혜안이 아니었을까 싶습니다.
10년안에 내 돈을 2배 만들어도 좋다시는 분은 이자율이 7%를 넘었을 때, 복리로 계속 재투자 해보시면 도움이 될 것 같습니다.
끝으로 파치올리의 명언을 남깁니다.(위키피디아 발췌)
72을 마음속에 법칙으로 지니고 있도록 해라.
'금융이야기' 카테고리의 다른 글
| ELS상환을 증권맨이 좌지우지한다?! (0) | 2022.11.18 |
|---|---|
| 키움 ELS 1호의 화끈한 신고식! (0) | 2022.11.17 |
| 고금리 보험 상품, "재매입 검토해 주소!" #3 (0) | 2022.05.31 |
| 고금리 보험 상품, "재매입 검토해 주소!" #2 (0) | 2022.05.29 |
| 고금리 보험 상품, "재매입 검토해 주소!" #1 (0) | 2022.05.28 |




댓글