이번 글에서는 European 풋옵션의 내재가치와 실제 프리미엄의 관계를 간단히 이야기해보도록 하겠습니다.
지난 글
2023.01.02 - [금융공학] - 풋옵션 시간가치의 비밀
풋옵션 시간가치의 비밀
이 글은 2022.12.30 - [금융공학] - 옵션, 시간은 내편!: 시간가치와 내재가치 옵션, 시간은 내편!: 시간가치와 내재가치 이 글에서는 European 콜/풋 옵션의 가격, 즉 프리미엄(premium)에 대한 여러가지
sine-qua-none.tistory.com
에서 풋옵션은 시간가치가 음수가 되는 영역, 즉
당장 권리 행사하는 것이(intrinsic value) 풋옵션 프리미엄보다 값어치 있는 영역
이 존재한다는 것을 보았습니다. 그래프로 그려보면,

위와 같이 되었죠.
이제 위의 그림에서 내재가치(intrinsic value)와 풋옵션 프리미엄이 교차하는 부분을 구해보도록 하겠습니다. 기호로는 아래그림과 같이 $S^\ast$로 쓰도록 하겠습니다.

그렇다면, 이자율 $r$이 양수일 때, 항상 저 점 $S^\ast$가 $0\leq S\leq K$사이에서 존재하는지를 판단해 보겠습니다.
유로피안 풋옵션 가격을 다시 환기시켜보면 다음과 같습니다.
$$p(t,S) = e^{-r\tau} K\Phi(-d_2) - S e^{-q\tau} \Phi(-d_1),\tag{1}$$
여기서 $$d_1= \frac{\ln(S/K)+(r-q+\frac12\sigma^2)\tau}{\sigma\sqrt{\tau}}, d_2= d_1 -\sigma \sqrt{\tau}$$
이고 $q$는 연속배당률, $\tau:=T-t$는 잔존만기, $\sigma$는 기초자산의 변동성, $\Phi(\cdot)$는 표준정규분포의 cdf입니다. 식(1)과 내재가치
$$\max(K-S,0)$$
의 차이를 $f$라 합시다. 즉, $f$는 시간가치이고,
$$ f(S) = e^{-r\tau} K\Phi(-d_2) - S e^{-q\tau} \Phi(-d_1) - \max(K-S,0)$$
입니다. 이 친구를 분석해 보기로 하죠.
$S^\ast$는 존재합니다.
우선
$$\lim_{S\rightarrow 0} f(S) < 0$$
을 증명하겠습니다. $S\rightarrow 0^+$ 일 때, $\ln(S/K)\rightarrow -\infty$이므로 $d_1, d_2 \rightarrow -\infty$ 입니다.
따라서 $-d_1 , -d_2 \rightarrow \infty$이고 $\Phi(-d_2) , \Phi(-d_1) \rightarrow 1$입니다. 즉,
$$ \lim_{S\rightarrow 0} p(t,S) = e^{-r\tau}K - Se^{-q\tau} \rightarrow e^{-r\tau}K~~~(\because S\rightarrow 0)$$입니다. 반면에 내재가치는
$$ \lim_{S\rightarrow 0} \max(K-S, 0) \rightarrow K$$
입니다. 또한 이자율이 양수이므로 $e^{-r\tau}<1$이죠. 따라서, $S$가 0 근처에서는
$$p(t,S) < \max(K-S,0)$$
즉, $f(0^+)<0$ 이죠
그리고 자명한 이야기지만, 풋옵션 프리미엄은 항상 양수입니다. 옵션 #2. 옵션 프리미엄 구하기(Closed form) 글에서도 다루었듯이
$$p(t,S) = e^{-r\tau} \mathbb{E} [ \max(K-S_T,0) ] \tag{2}$$
을 푼 식이 바로 식(1)이고 식 (2)는 항상 양수인 $\max(K-S_T,0)$ 인 확률 변수의 기댓값으로 표현되기 때문에 양수가 나올 수밖에 없죠.
따라서 특별히 $S=K$일 때, 즉 ATM(at the money, 등가격) 일 때도 $p(t,K)$는 양수입니다. 따라서
$f(K) >0$입니다.
따라서, 중간값정리(위키 참조)에 의해 $f(S^\ast)=0$ 즉,
$$ p(t,S^\ast) =\max(K-S^\ast,0) ~~,~~0<S^\ast <K$$
인 $S^\ast$가 존재하게 됩니다.
$S^\ast$ 찾기: python code
재미 삼아, $S^\ast$가 어떤 특징을 가지는지 한번 살펴보겠습니다.
위에서 함수 $f$가 $0$과 $K$사이에서 근을 가진다고 했고, 이 근을 $S^\ast$라 했습니다. 따라서 내재가치를 $K-S$로 봐도 무방합니다. 이때,
$$f(S) = p(t,S) -(K-S)$$ 의 해를 구하는 것이 목표인데, 2차방정식처럼 근의 공식이 있는 것도 아니고 해를 찾기가 굉장히 난해합니다. 이 때 쓰는 방법이 있었죠. 바로
[수학의 재미/아름다운 이론] - 해를 향하여 #1 : Bisection Method 또는
[수학의 재미/아름다운 이론] - 해를 향하여 #2: Newton-Raphson Method 입니다.
이 중, Bisection Method는 해가 있을만한 구간을 절반씩 줄여나가면서 결국엔 해의 근사치를 찾는 방법인데, 위의 함수 $f$처럼 복잡한 함수의 해를 찾는데 적합합니다.
아래 코드를 볼까요? 간단한 설명은 주석을 참고하시기 바랍니다.
# bisection method로 해찾는 함수
def my_bisection(f, a, b, tol):
# approximates a root, R, of f bounded
# by a and b to within tolerance
# | f(m) | < tol with m the midpoint
# between a and b Recursive implementation
# check if a and b bound a root
if np.sign(f(a)) == np.sign(f(b)):
raise Exception(
"The scalars a and b do not bound a root")
# get midpoint
m = (a + b) / 2
if np.abs(f(m)) < tol:
# stopping condition, report m as root
return m
elif np.sign(f(a)) == np.sign(f(m)):
# case where m is an improvement on a.
# Make recursive call with a = m
return my_bisection(f, m, b, tol)
elif np.sign(f(b)) == np.sign(f(m)):
# case where m is an improvement on b.
# Make recursive call with b = m
return my_bisection(f, a, m, tol)
def find_putPremium_instrinsic_cross():
s0 = 100
strike = 100
maturity = 1
rfr = 0.02
vol = 0.3
div = 0.01
vol_step = 0.01
vol_vec = np.arange(0.1, 0.5 + vol_step, vol_step)
# vol : 10% ~ 50% 사이 1%pt 증가
strike_step = 1
strike_vec = np.arange(10, 100 + strike_step, strike_step)
# strike : 10 ~100 사이 1씩 증가
maturity_step = 0.25
maturity_vec = np.arange(0.25, 5 + maturity_step, maturity_step)
# 만기: 3M - 5Y 사이 3M씩 증가
tol = 10 ** -5 #bisection method 의 tolerance 설정
s_tgt_vec = []
error_vec = []
s_min, s_max = 0.01, strike
for v in vol_vec:
put_premium = lambda x: PutOptionBS(x, strike, maturity, rfr, div, v) - (strike - x)
# 글에서 정의한 함수 f(S)
s_tgt = my_bisection(put_premium, s_min, s_max, tol)
# 0<S<행사가 범위에서 해를 찾음
error = PutOptionBS(s_tgt, strike, maturity, rfr, div, v) - (strike - s_tgt)
# 찾은 해를 함수 f에 넣어서 진짜 해가 맞는지 검증
s_tgt_vec.append(s_tgt)
error_vec.append(error)
plt.subplot(1, 3, 1)
plt.plot(vol_vec, s_tgt_vec, label='vol vs s*', color='b')
plt.xlabel('vol')
plt.legend()
s_tgt_vec = []
for k in strike_vec:
put_premium = lambda x: PutOptionBS(x, k, maturity, rfr, div, vol) - (k - x)
s_tgt = my_bisection(put_premium, s_min, k, tol)
# s_max 대신 k를 s_max로 했음에 주목: strike를 움직이는 상황이라..
s_tgt_vec.append(s_tgt)
plt.subplot(1, 3, 2)
plt.plot(strike_vec, s_tgt_vec, label='strike vs s*', color='c')
plt.xlabel('strike')
plt.legend()
s_tgt_vec = []
for m in maturity_vec:
put_premium = lambda x: PutOptionBS(x, strike, m, rfr, div, vol) - (strike - x)
s_tgt = my_bisection(put_premium, s_min, s_max, tol)
s_tgt_vec.append(s_tgt)
plt.subplot(1, 3, 3)
plt.plot(maturity_vec, s_tgt_vec, label='maturity vs s*', color='m')
plt.xlabel('maturity')
plt.legend()
plt.show()
즉, 변동성, 행사가, 만기를 각각 움직여가면서 해를 찾은 것입니다. 각 상황별로 다른 파라미터들은 고정입니다. 예를 들어 아래 첫 번째 그림의 경우, 변동성별로 $S^\ast$를 찾는 것인데, 이때, 만기, 행사가, 배당률, 이자율 등 다른 파라미터는 모두 고정입니다(고정된 상수값은 위 python code에 나와 있습니다.)
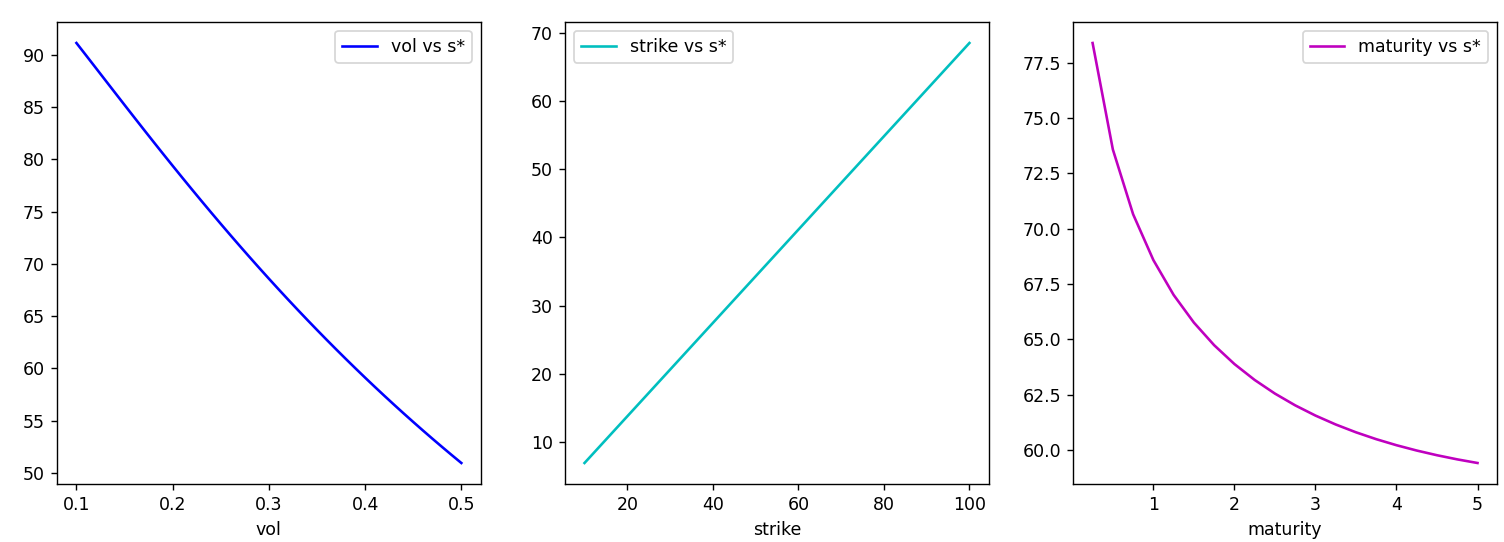
결과를 분석해 볼까요?
| ○ | 변동성이 클수록 $S^\ast$ 값은 작아지고, 변동성이 작으면 $S^\ast$는 행사가에 가까워집니다. Why? 변동성이 작으면 기초자산 움직임이 조용하다는 이야기이고, 그러면 바로 권리 행사했을 때 얻는 가치가 더 커지게 되는거죠. 어차피 횡보하는 상황에서 더 기다려봤자, 더 좋은 행사가치를 기대하기 어렵기 때문입니다. |
| ○ | 행사가가 클수록 $S^\ast$ 가 커집니다. Why? 일견 당연한 내용처럼 보입니다. 행사가가 커지면 거기에 비례해서 시간가치가 0이 되는 지점이 더 늘어나게 되는거죠. 이 현상에 대해서는 아래서 좀 더 자세하게 다루겠습니다 |
| ○ | 만기가 길수록 $S^\ast$ 가 작아집니다. Why? 만기가 길면 아직 기초자산의 만기 종가가 결정되기 까지 많은 시간적 여유가 있습니다. 따라서 으레 풋옵션 가치는 커지겠죠. 따라서 바로 권리 행사했을때 가치가 높아지는 경우가 줄어듭니다. 즉 $S^\ast$가 작아지는 방향입니다. |
$S^\ast$와 행사가의 관계
위 [그림 1]의 중간 그래프를 보시죠. 행사가 별 $S^\ast$가 마치 직선을 이루는 것처럼 보입니다. 회귀분석을 통해 엄밀히 해볼까요?
위 코드를 중간 그래프만 나오게끔 수정하고, 회귀분석 과정을 추가해 보겠습니다.
# linear regression을 위한 sklearn libarary 이용
# LinearRegression library
from sklearn.linear_model import LinearRegression
def find_putPremium_instrinsic_cross():
s0 = 100
strike = 100
maturity = 1
rfr = 0.02
vol = 0.3
div = 0.01
strike_step = 1
strike_vec = np.arange(10, 100 + strike_step, strike_step)
s_min, s_max = 0.01, strike
tol = 10 ** -5
s_tgt_vec = []
for k in strike_vec:
put_premium = lambda x: PutOptionBS(x, k, maturity, rfr, div, vol) - (k - x)
s_tgt = my_bisection(put_premium, s_min, k, tol)
s_tgt_vec.append(s_tgt)
plt.plot(strike_vec, s_tgt_vec, label='strike vs s*', color='c')
plt.xlabel('strike')
plt.legend()
# y_train = a * X_train + b
# 를 만족하는 a, b를 구할 예정
# a: weight coefficient(가중치) 또는 slope(기울기)라 부름
# b : intercept (y절편) 이라 부름
X_train = strike_vec.reshape(-1, 1) # linear regression을 위한 X data형식
y_train = np.array(s_tgt_vec).reshape(-1, 1) # linear regression을 위한 y data형식
model = LinearRegression() # 선형 모델을 선택
model.fit(X_train, y_train) # 회귀분석 실행 (fit)
score = model.score(X_train, y_train) # model의 score (R square) 계산
w = model.coef_ # 가중치 계산
b = model.intercept_ # y절편(intercept) 계산
print('weight: ', w)
print('intercept: ', b)
print('R2 : ', round(score, 3))
plt.show()
결과는 아래와 같습니다.
weight: [[0.68583875]]
intercept: [4.36916949e-06]
R2 : 1.0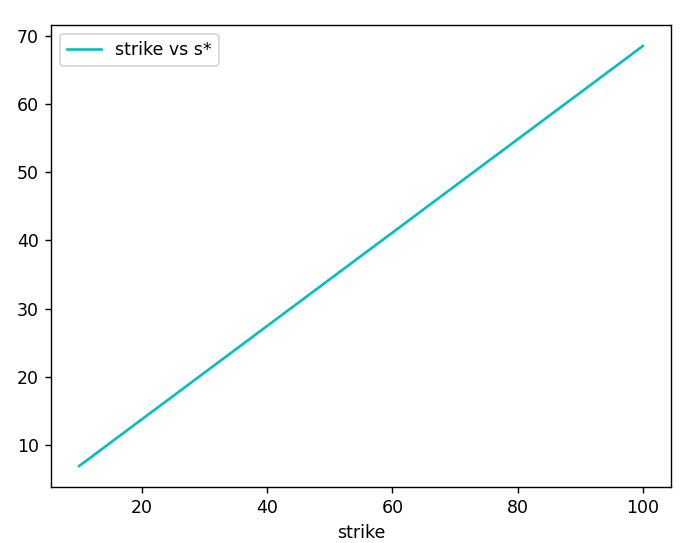
위 결과를 종합해 보면, 행사가 $K$와 $S^\ast$의 관계는
$$ S^\ast = wK + b $$이고 $w=0.686 , b \approx 0$ 이므로
$$ S^\ast= 0.686 K$$
입니다. 이 회귀분석의 R-square는 1입니다. 즉, 완전 선형의 관계가 있다는 이야기겠죠. 이론적으로 설명하면 아래의 이유 때문입니다.
점 $S^\ast$는 함수 $f$, 즉 $p(t,S)=(K-S)$의 해라고 했습니다. 즉, $S^\ast$는
$$e^{-r\tau} K\Phi(-d_2) - S e^{-q\tau} \Phi(-d_1)-(K-S) =0$$
의 해입니다.
따라서 $x=S/K$ 라 하면 $x$는
$$e^{-r\tau} \Phi(-d_2) - x e^{-q\tau} \Phi(-d_1)-(1-x) =0 \tag{3}$$
의 해입니다. 또한
$$d_1= \frac{\ln(x)+(r-q+\frac12\sigma^2)\tau}{\sigma\sqrt{\tau}}, d_2= d_1 -\sigma \sqrt{\tau}$$
입니다.
식(3)은 $S$와 $K$에 관계없는 $x$에 대한 함수이고 이 식의 근 $x^\ast$를 구할 수 있겠죠.
따라서, $ S/K = x^\ast$ 즉,
$$ S= x^\ast K $$
가 바로 함수 $f$의 근이 되는 것입니다.
위의 예제에서 $x^\ast = 0.686$인 셈인 것이죠.
즉 $S$가 $S/K$로 치환되며 degenerated 되므로 $S^\ast$와 $K$는 비례관계가 있는 것입니다.
'금융공학' 카테고리의 다른 글
| 2Star WorstPerform 풋옵션 가격: 시뮬레이션 (0) | 2023.01.15 |
|---|---|
| 여러개의 기초자산을 가지는 파생상품 가격결정식 (0) | 2023.01.13 |
| 유로피안옵션과 아메리칸옵션이 같을 때는?(feat. 이항트리) (0) | 2023.01.06 |
| 배당 없는 주식을 살 권리는 아메리칸 스타일이 곧 유로피안 스타일! (0) | 2023.01.05 |
| 옵션 시간가치 쩌는 곳은? (2) | 2023.01.03 |




댓글