이 글에서는 아메리칸 옵션(American option)의 재미있는 특징을 알아볼까 합니다. 이전의 글
아메리칸 옵션의 평가 #3 : 함축적(implicit) FDM
에서 고찰해 본 바에 의하면, 아메리칸 옵션은 만기 전 아무 시점에나 권리 행사가 가능하기에 유로피언 옵션보다 프리미엄이 비쌉니다. 그러면
아메리칸 옵션이 유로피안 옵션보다 항상 비싼가?
위 질문이 궁금해집니다. 일단 코드를 통해 알아보기로 하죠.
아메리칸/유로피안 가격 비교를 위한 python code
이전 글에서 작성했던 아메리칸 옵션을, 콜/풋옵션과 아메리칸/유로피안 스타일을 파라미터로 넣어 계산 가능한 코드로 업데이트하였습니다.
import numpy as np
import matplotlib.pyplot as plt
def VanillaOption_BinomialTree(s0, strike, maturity, rfr, div, vol, opttype, exertype):
# opttype : call(C)/put(P) 선택 파라미터 추가
# exertype : American(A) / European(E) 선택 파라미터 추가
nNode = 200
dt = maturity / nNode
u = np.exp(vol * np.sqrt(dt))
d = 1 / u
a = np.exp((rfr - div) * dt)
p = (a - d) / (u - d)
if opttype.upper() == 'C': # opttype의 대문자가 'C'이면, call option
exer_payoff = lambda x: max(x - strike, 0) # call opt 만기payoff
elif opttype.upper() == 'P': # opttype의 대문자가 'P'이면, put option
exer_payoff = lambda x: max(strike - x, 0) # put opt 만기 payoff
else:
exer_payoff = -999
cnt = 0 # 연속가치와 행사가치가 swithcing 되는 횟수 counting
total_cnt = 0 # 전체 이항트리의 노드 계산 횟수
valueNode = np.zeros((nNode + 1, nNode + 1))
for n in reversed(range(nNode + 1)):
for i in range(n + 1):
total_cnt += 1
spotS = s0 * u ** i * d ** (n - i)
if n == nNode:
valueNode[n, i] = exer_payoff(spotS) # end node에 만기 payoff 대입
else:
up_val = valueNode[n + 1, i + 1]
down_val = valueNode[n + 1, i]
df = np.exp(-rfr * dt)
conti_val = (p * up_val + (1 - p) * down_val) * df
exer_val = exer_payoff(spotS) # 각 node에서 행사가치
valueNode[n, i] = max(conti_val, exer_val) if exertype.upper() == 'A' else conti_val
# American/European 여부에 따라 node 값 계산
if (exertype.upper() == 'A') & (exer_val > conti_val):
cnt += 1 #American 이고 행사가치 > 연속가치여서 payoff switching 일어나는 경우
if exertype.upper() == 'A':
print('Exer/Continuation Value Switching Ratio:{:.2f}, when spot={}'.format(cnt / total_cnt, s0))
# cnt/total_cnt 출력하여 스위칭되는 빈도 관찰
return valueNode[0, 0]자세한 설명은 주석을 참고하시기 바랍니다.
콜옵션의 경우: 이자율 양수, 배당률 양수
참, 예전에 이런 분석을 할 때는 으레 이자율은 당연히 양수라고 가정하고 접근할 때가 많았는데요. 2010년 대 중반을 거쳐 오면서 마이너스 금리가 꽤 익숙해질 정도가 되었죠. 우선 이 관찰에서는 이자율을 양수라 합시다.
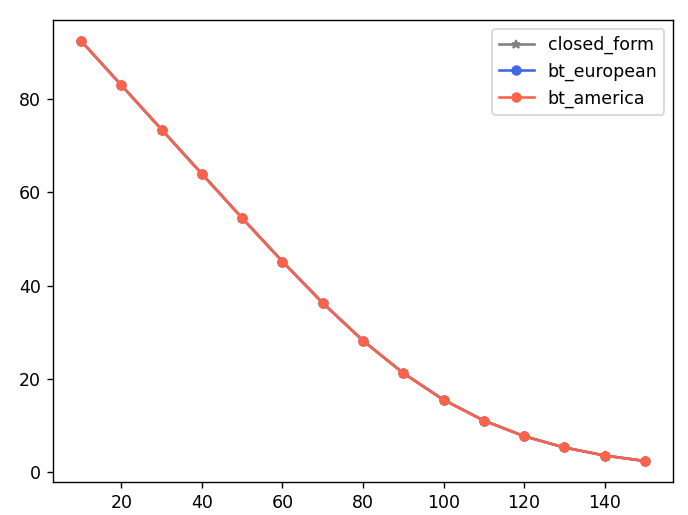
아래 코드로 Vanilla option의 European, American 스타일 계산을 해보도록 할게요. European 이항트리 방법이 잘 계산됐는지 확인을 위해 Closed form (함수 CallOptionBS)도 같이 그려봅니다
def Compare_Eur_Amer_Call():
s0 = 100
strike = 100
maturity = 1
rfr = 0.02
vol = 0.3
div = 0.05
opt_type = 'C'
s_vec = np.arange(10, 151, 10)
exact_value = np.array([CallOptionBS(s, strike, maturity, rfr, div, vol) for s in s_vec])
bt_value_eur = np.array(
[VanillaOption_BinomialTree(s, strike, maturity, rfr, div, vol, opt_type, 'E') for s in s_vec])
bt_value_amer = np.array(
[VanillaOption_BinomialTree(s, strike, maturity, rfr, div, vol, opt_type, 'A') for s in s_vec])
plt.plot(s_vec, exact_value, color='gray', marker='*', markersize=5, label='closed_form')
plt.plot(s_vec, bt_value_eur, color='royalblue', marker='o', markersize=5, label='bt_european')
plt.plot(s_vec, bt_value_amer, color='tomato', marker='o', markersize=5, label='bt_america')
plt.legend()
plt.show()
배당률 div를 0.05로 잡은 예입니다. 결과를 보면,
Exer/Continuation Value Switching Ratio:0.08, when spot=10
Exer/Continuation Value Switching Ratio:0.16, when spot=20
Exer/Continuation Value Switching Ratio:0.21, when spot=30
Exer/Continuation Value Switching Ratio:0.26, when spot=40
Exer/Continuation Value Switching Ratio:0.29, when spot=50
Exer/Continuation Value Switching Ratio:0.33, when spot=60
Exer/Continuation Value Switching Ratio:0.36, when spot=70
Exer/Continuation Value Switching Ratio:0.38, when spot=80
Exer/Continuation Value Switching Ratio:0.41, when spot=90
Exer/Continuation Value Switching Ratio:0.43, when spot=100
Exer/Continuation Value Switching Ratio:0.45, when spot=110
Exer/Continuation Value Switching Ratio:0.47, when spot=120
Exer/Continuation Value Switching Ratio:0.49, when spot=130
Exer/Continuation Value Switching Ratio:0.50, when spot=140
Exer/Continuation Value Switching Ratio:0.52, when spot=150
역시, 아메리칸 옵션이 유로피안에 비해 프리미엄이 쎄다는 것이 확인이 됩니다. 위의 연속가치/행사가치 결과를 봐도 ATM부근에서는 약 40%의 확률로 더 행사가치가 크게 나타나는 노드들이 있다는 것을 볼 수 있습니다.
배당률이 0이면 어떻게 될까요?
콜옵션의 경우: 이자율 양수, 배당률 없음
위 코드에서 파라미터 인풋만 바꿔줍니다.
strike = 100
maturity = 1
rfr = 0.02
vol = 0.3
div = 0 #배당률 0
opt_type = 'C'
결과는 아래와 같습니다.
Exer/Continuation Value Switching Ratio:0.00, when spot=10
Exer/Continuation Value Switching Ratio:0.00, when spot=20
Exer/Continuation Value Switching Ratio:0.00, when spot=30
Exer/Continuation Value Switching Ratio:0.00, when spot=40
Exer/Continuation Value Switching Ratio:0.00, when spot=50
Exer/Continuation Value Switching Ratio:0.00, when spot=60
Exer/Continuation Value Switching Ratio:0.00, when spot=70
Exer/Continuation Value Switching Ratio:0.00, when spot=80
Exer/Continuation Value Switching Ratio:0.00, when spot=90
Exer/Continuation Value Switching Ratio:0.00, when spot=100
Exer/Continuation Value Switching Ratio:0.00, when spot=110
Exer/Continuation Value Switching Ratio:0.00, when spot=120
Exer/Continuation Value Switching Ratio:0.00, when spot=130
Exer/Continuation Value Switching Ratio:0.00, when spot=140
Exer/Continuation Value Switching Ratio:0.00, when spot=150
스위칭되는 노드가 하나도 없네요! 차트를 보시면
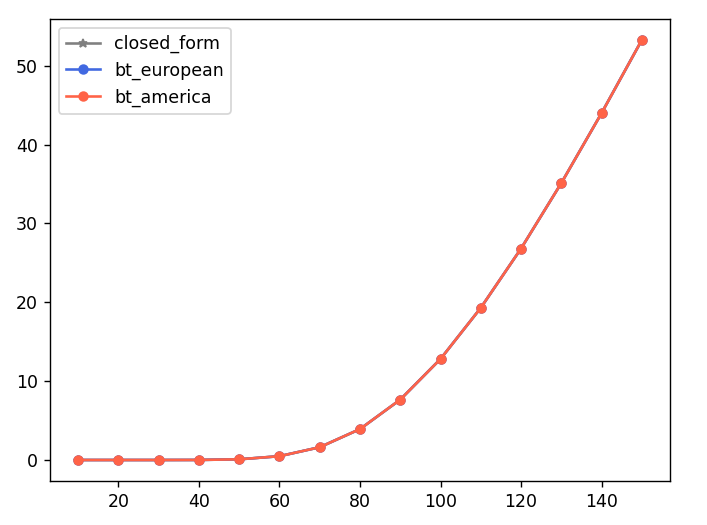
차트를 보니, 아메리칸옵션과 유로피안 옵션 가격이 똑같네요. 스위칭의 경우가 없으니, 즉, 연속가치가 행사가치보다 크니 유로피안 옵션과 아메리칸 옵션의 가격이 같습니다.
이자율이 음수면 어떨까요?
콜옵션의 경우: 이자율 음수
strike = 100
maturity = 1
rfr = -0.02 # 이자율 음수
vol = 0.3
div = 0
opt_type = 'C'
연속배당률은 0으로 가정하고 무위험 이자율은 음수입니다. 결과는 아래와 같습니다.
Exer/Continuation Value Switching Ratio:0.08, when spot=10
Exer/Continuation Value Switching Ratio:0.15, when spot=20
Exer/Continuation Value Switching Ratio:0.20, when spot=30
Exer/Continuation Value Switching Ratio:0.25, when spot=40
Exer/Continuation Value Switching Ratio:0.28, when spot=50
Exer/Continuation Value Switching Ratio:0.32, when spot=60
Exer/Continuation Value Switching Ratio:0.34, when spot=70
Exer/Continuation Value Switching Ratio:0.37, when spot=80
Exer/Continuation Value Switching Ratio:0.39, when spot=90
Exer/Continuation Value Switching Ratio:0.41, when spot=100
Exer/Continuation Value Switching Ratio:0.43, when spot=110
Exer/Continuation Value Switching Ratio:0.45, when spot=120
Exer/Continuation Value Switching Ratio:0.47, when spot=130
Exer/Continuation Value Switching Ratio:0.49, when spot=140
Exer/Continuation Value Switching Ratio:0.50, when spot=150스위칭되는 걸 보니, 아메리칸 옵션과 유로피안 옵션 가격에 차이가 발생하겠네요.
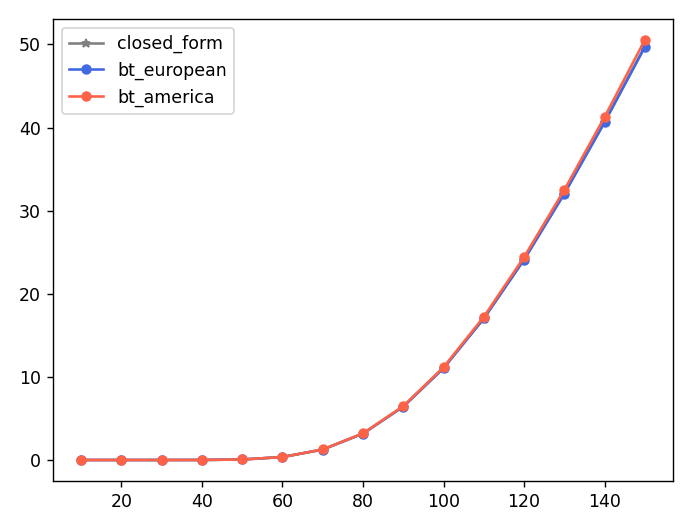
조금 차이가 발생하는 게 보입니다.
그렇다면 풋옵션은 어떤지 보겠습니다.
풋옵션 비교를 위해서 위의 코드 중
exact_value = np.array([CallOptionBS(s, strike, maturity, rfr, div, vol) for s in s_vec])이 부분을
exact_value = np.array([PutOptionBS(s, strike, maturity, rfr, div, vol) for s in s_vec])으로 바꿔주면 됩니다.
풋옵션의 경우: 이자율 양수, 배당률 양수
배당률은 콜옵션 관찰 때처럼 0.05로 두겠습니다.
Exer/Continuation Value Switching Ratio:0.75, when spot=10
Exer/Continuation Value Switching Ratio:0.62, when spot=20
Exer/Continuation Value Switching Ratio:0.54, when spot=30
Exer/Continuation Value Switching Ratio:0.47, when spot=40
Exer/Continuation Value Switching Ratio:0.42, when spot=50
Exer/Continuation Value Switching Ratio:0.38, when spot=60
Exer/Continuation Value Switching Ratio:0.35, when spot=70
Exer/Continuation Value Switching Ratio:0.33, when spot=80
Exer/Continuation Value Switching Ratio:0.31, when spot=90
Exer/Continuation Value Switching Ratio:0.29, when spot=100
Exer/Continuation Value Switching Ratio:0.27, when spot=110
Exer/Continuation Value Switching Ratio:0.26, when spot=120
Exer/Continuation Value Switching Ratio:0.24, when spot=130
Exer/Continuation Value Switching Ratio:0.23, when spot=140
Exer/Continuation Value Switching Ratio:0.22, when spot=150ITM 영역에서 엄청 스위칭이 되네요. 차트는 아래와 같습니다.
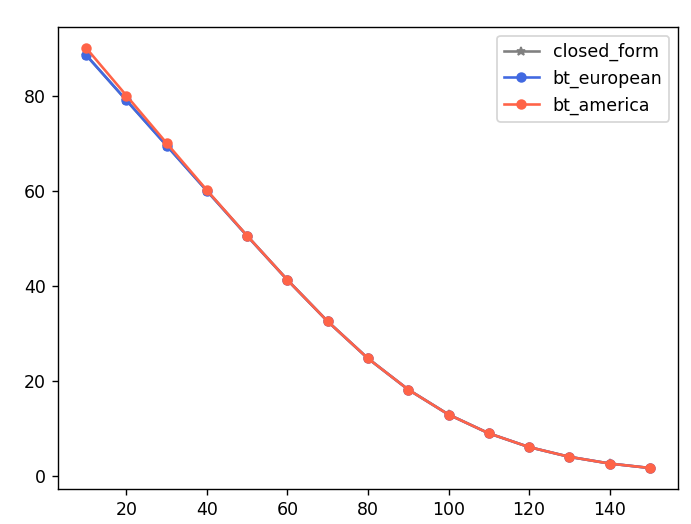
풋옵션의 경우: 이자율 양수, 배당률 없음
Exer/Continuation Value Switching Ratio:0.85, when spot=10
Exer/Continuation Value Switching Ratio:0.75, when spot=20
Exer/Continuation Value Switching Ratio:0.68, when spot=30
Exer/Continuation Value Switching Ratio:0.62, when spot=40
Exer/Continuation Value Switching Ratio:0.57, when spot=50
Exer/Continuation Value Switching Ratio:0.53, when spot=60
Exer/Continuation Value Switching Ratio:0.50, when spot=70
Exer/Continuation Value Switching Ratio:0.47, when spot=80
Exer/Continuation Value Switching Ratio:0.44, when spot=90
Exer/Continuation Value Switching Ratio:0.42, when spot=100
Exer/Continuation Value Switching Ratio:0.40, when spot=110
Exer/Continuation Value Switching Ratio:0.38, when spot=120
Exer/Continuation Value Switching Ratio:0.37, when spot=130
Exer/Continuation Value Switching Ratio:0.35, when spot=140
Exer/Continuation Value Switching Ratio:0.34, when spot=150아메리칸 콜옵션과 달리 스위칭이 빈번하게 발생하네요. 차트는 아래와 같습니다.
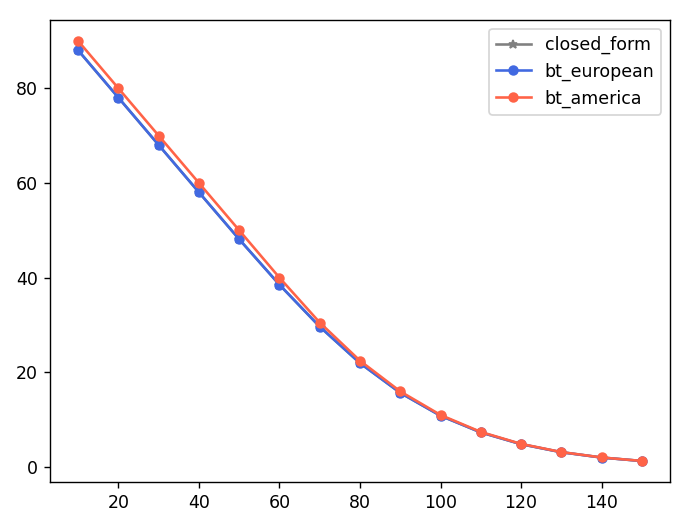
풋옵션의 경우: 이자율 음수
이자율을 -2%, 배당률을 5% 로 두어봤습니다. 그런데
Exer/Continuation Value Switching Ratio:0.00, when spot=10
Exer/Continuation Value Switching Ratio:0.00, when spot=20
Exer/Continuation Value Switching Ratio:0.00, when spot=30
Exer/Continuation Value Switching Ratio:0.00, when spot=40
Exer/Continuation Value Switching Ratio:0.00, when spot=50
Exer/Continuation Value Switching Ratio:0.00, when spot=60
Exer/Continuation Value Switching Ratio:0.00, when spot=70
Exer/Continuation Value Switching Ratio:0.00, when spot=80
Exer/Continuation Value Switching Ratio:0.00, when spot=90
Exer/Continuation Value Switching Ratio:0.00, when spot=100
Exer/Continuation Value Switching Ratio:0.00, when spot=110
Exer/Continuation Value Switching Ratio:0.00, when spot=120
Exer/Continuation Value Switching Ratio:0.00, when spot=130
Exer/Continuation Value Switching Ratio:0.00, when spot=140
Exer/Continuation Value Switching Ratio:0.00, when spot=150
스위칭이 안되네요. 당연히 차트를 관찰하면 아메리카 옵션가격과 유로피안 옵션가격이 같을 것입니다.
결과
결과를 정리해보자면
콜옵션
| 이자율 / 배당률 | 0 | 양수 |
| 음수 | 아메리칸 = 유로피안 | |
| 양수 |
표시 안 한 부분은 아메리칸 옵션이 유로피안보다 큽니다.
풋옵션
| 이자율 / 배당률 | 0 | 양수 |
| 음수 | 아메리칸 = 유로피안 | 아메리칸 = 유로피안 |
| 양수 |
위와 같이 나오는 듯합니다.
즉 통념적으로 우리가 이자율이 양수인 세상에서 살고 있다고 생각하는 상황에서,
배당률이 0인 주식을 기초자산으로 하는 콜옵션은 아메리칸 옵션과 유로피안 옵션의 가격이 같다!

보다 자세한 사항을 다음글에서 수식을 써서 한번 알아보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 풋옵션 시간가치가 없어지는 영역은? (0) | 2023.01.11 |
|---|---|
| 유로피안옵션과 아메리칸옵션이 같을 때는?(feat. 이항트리) (0) | 2023.01.06 |
| 옵션 시간가치 쩌는 곳은? (2) | 2023.01.03 |
| 풋옵션 시간가치의 비밀 (0) | 2023.01.02 |
| 옵션, 시간은 내편!: 시간가치와 내재가치 (0) | 2022.12.30 |




댓글