이 글은
2022.12.30 - [금융공학] - 옵션, 시간은 내편!: 시간가치와 내재가치
옵션, 시간은 내편!: 시간가치와 내재가치
이 글에서는 European 콜/풋 옵션의 가격, 즉 프리미엄(premium)에 대한 여러가지 사실을 알아보도록 하겠습니다. European 옵션의 경우 Black Scholes formula라는 수식이 존재했었죠. 옵션 #2. 옵션 프리미엄
sine-qua-none.tistory.com
에서 이어집니다.
저번 글에서는 옵션이 내재가치(intrinsic value)와 시간가치(time premium)로 나뉘고 콜옵션의 프리미엄은 항상 내재가치보다 크다, 즉 시간 가치가 항상 양수라는 간단한 설명을 했습니다.
복습: 옵션의 내재가치와 시간가치
콜/풋옵션은 내재가치와 시간가치로 나뉜다고 하였습니다. 내재가치와 시간가치를 복습하자면,
내재가치는 옵션을 당장 권리 행사했을 때 얻을 수 있는 수익을 뜻하고, 시간가치는 옵션 프리미엄에서 내재가치를 뺀 값을 의미합니다. 즉, 만기까지 남은 시간 동안 수익이 발생할 가능성 때문에 생기는 가치입니다. 시점 $t$에서의 기초자산 가격을 $S_t$, 행사가를 $K$라 하면, 옵션의 내재가치는
| 구분 | 내재가치 |
| 콜옵션 | $\max(S_t-K,0)$ |
| 풋옵션 | $\max(K-S_t,0)$ |
가 됩니다. 또한 Black Scholes Formula에 따르면 시점 $t$의 기초자산 가격이 $S_t$인 상황에서 콜옵션 프리미엄 $c(t,S_t)$와 풋옵션 프리미엄 $p(t, S_t)$는 각각
| 구분 | 가격공식(closed form) |
| 콜옵션 | $c(t,S_t) = S_t e^{-q\tau} \Phi(d_1) -Ke^{-r\tau}\Phi(d_2)$ |
| 풋옵션 | $p(t,S_t) = Ke^{-r\tau}\Phi(-d_2) - S_t e^{-q\tau}\Phi(-d_1)$ |
| - $r, q, \sigma$ : 각각 무위험이자율, 연속배당률, 기초자산 변동성 - $ d_1 =\frac{\ln(S_t/K)+(r-q+{\textstyle\frac12}\sigma^2)\tau}{\sigma\sqrt{\tau}}, ~ d_2 = d_2-\sigma\sqrt{\tau}$ - $\tau = T- t$ , 즉 $\tau$는 잔존만기, $T$는 옵션 만기 - $\Phi(\cdot) $ : 표준정규분포의 cdf |
|
위와 관련된 자세한 설명은 옵션 #2. 옵션 프리미엄 구하기(Closed form)를 참고하시기 바랍니다.
따라서 위 둘을 종합해 보면, 옵션의 시간가치는 각각
| 구분 | 시간가치 |
| 콜옵션 | $c(t,S_t) - \max(S_t-K,0)$ |
| 풋옵션 | $p(t,S_t)-\max(K-S_t,0)$ |
입니다.
복습: 콜옵션의 프리미엄과 내재가치, 시간가치
지난 글에서 우리는 아래의 그래프를 관찰할 바 있습니다.

파란색 선이 콜옵션 프리미엄이고, 빨간색 선이 내재가치입니다.그 차이인 회색 영역이 바로 시간가치입니다.
그림으로도 보이듯이 시간가치는 항상 양수입니다. 반면에 풋옵션은 좀 다릅니다.
풋옵션의 시간 가치는 음수가 되는 부분이 있다!?!?
풋옵션의 시간가치의 비밀
먼저 python code를 통하여 풋옵션의 시간가치에 대해서 알아보기로 하죠.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import time
N = norm.cdf
def PutOptionBS(S, K, T, r, q, sigma):
if T == 0:
return np.max(K - S, 0)
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
return -S * np.exp(-q * T) * N(-d1) + K * np.exp(-r * T) * N(-d2)
def Put_option_and_intrinsic_value():
s0 = 100
strike = 100
maturity = 1
rfr = 0.02
vol = 0.4
div = 0.01
s_vec = np.arange(10, 301, 1)
numS = 80
exact_value = np.array([PutOptionBS(s, strike, maturity, rfr, div, vol) for s in s_vec])
intrinsic_value = np.maximum(strike - s_vec, 0)
plt.subplot(1, 2, 1)
plt.title('put option premium & intrinsic value')
plt.plot(s_vec, exact_value, color='gray', label='put premium')
plt.plot(s_vec, intrinsic_value, color='royalblue', label='put intrinsic value')
plt.fill_between(s_vec, exact_value, intrinsic_value, color='limegreen', alpha=0.5)
plt.legend()
plt.subplot(1, 2, 2)
plt.title('Zoom In graph')
plt.plot(s_vec[:numS], exact_value[:numS], color='gray', label='put premium')
plt.plot(s_vec[:numS], intrinsic_value[:numS], color='royalblue', label='put intrinsic value')
plt.fill_between(s_vec[:numS], exact_value[:numS], intrinsic_value[:numS],
where=(exact_value[:numS] < intrinsic_value[:numS]), color='tomato', alpha=0.5)
plt.legend()
plt.tight_layout
plt.show()
if __name__ == '__main__':
Put_option_and_intrinsic_value()
code는 간단하므로 설명은 생략하도록 하겠습니다. 결과를 보겠습니다.
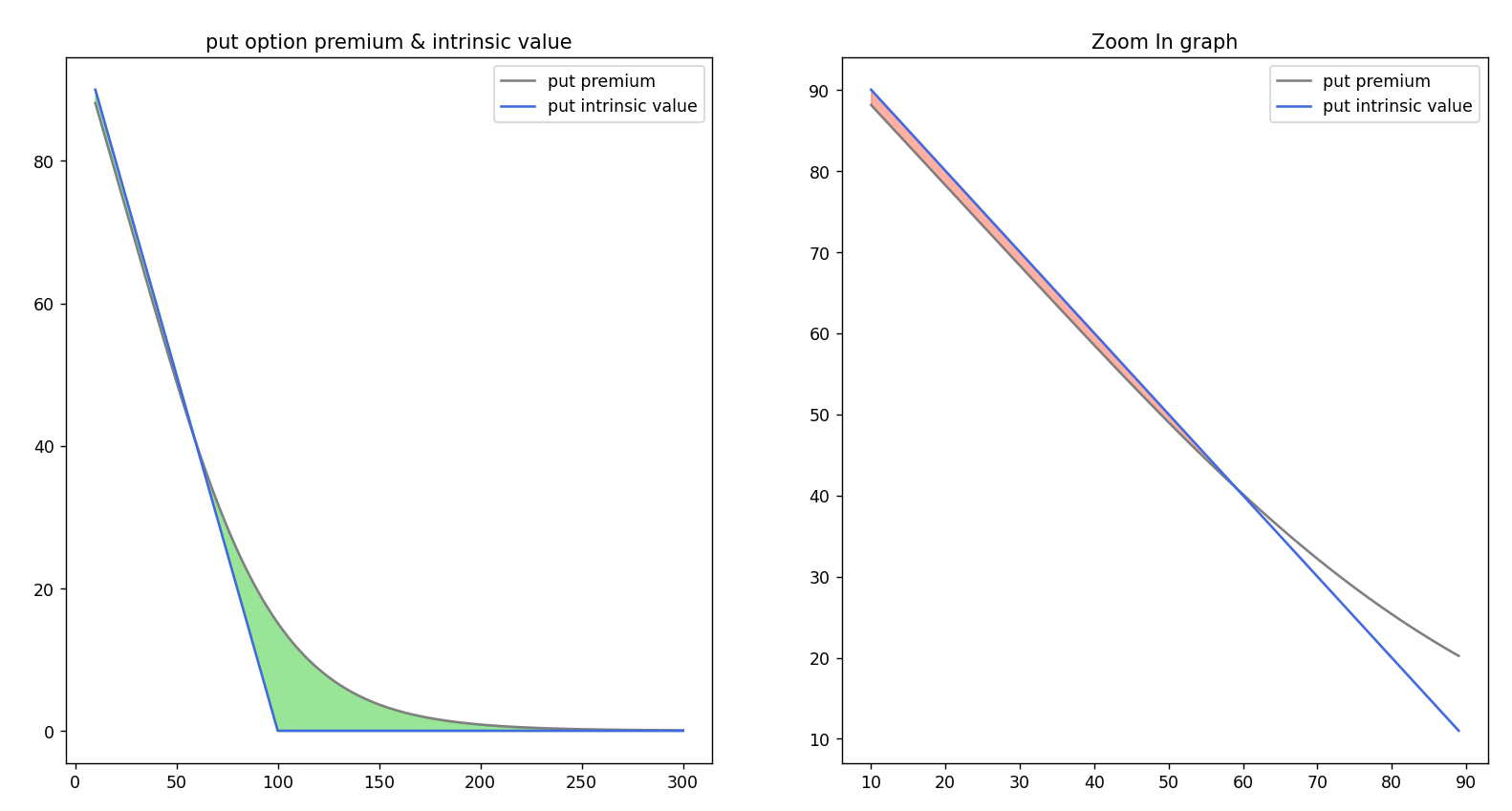
위 그래프를 보시죠. 콜옵션과 달리 내재가치가 풋옵션 프리미엄 그래프를 뚫고 올라가는 영역이 있습니다. 주가 60 부근에서 역전되어 60보다 기초자산 레벨이 하회하는 방향으로 내재가치가 더 큽니다.
즉 시간가치가 마이너스가 되는거죠. 즉
풋옵션의 시간가치가 음수인 영역이 있다!!
이죠.
그림에서 보듯이 ITM 영역, 즉, 당장 권리행사했을 때 수익이 나는 영역 중에서 아주 큰 내재가치가 가장된 부분(이를 Deep ITM이라 합니다.) 쪽에서 내재 가치가 더 큽니다.
한 가지 의문스러운 사실은, 콜옵션의 시간가치가 항상 양수임을 설명할 때, 잔존만기동안에 주가가 오를 기대감으로 콜옵션 프리미엄이 더 커진다는 사실이 풋옵션에서는 통하지 않는 걸까요?
그렇습니다.
주식은 끝없이 오를 순 있어도, 끝없이 빠질 순 없다. 주식값이 마이너스는 될 수 없으므로..
의 이유 때문입니다. 기초자산 가격은 위의 상한선이 없습니다. 끝없이 오를 기대감으로 콜옵션 가격은 내재가치보다 항상 커지기 마련입니다. 그런데, 주식은 휴지조각, 즉 0원이 하한선이죠. 끝없이 빠질 수가 없는 노릇입니다.
따라서 기초자산이 휴지조각이 되면 그때 바로 행사할 수 있다면 권리를 누리는 것이 최고 이득일 것입니다. 굳이 시간가치를 노린다고 더 기다려봤자. 주식은 휴지에서 오를 일만 있으므로 페이오프는 줄어들게 마련입니다.
이러한 현상 때문에 풋옵션 프리미엄은 아주 작은 기초자산 레벨 수준에서는 내재가치를 넘어설 수 없는, 즉, 만기까지 시간이 남았다고 능사가 아닌 상황이 있다는 거죠. 이는 아래와 같이 수식으로도 증명이 됩니다.
기초자산이 휴지일 때, 풋옵션 프리미엄은?
일반적인 상황: 무위험이자율이 양수일 때,
기초자산 $S_t \rightarrow 0$ 인 상황을 가정해 보면,
$$ p(t,S_t) = e^{-r\tau} K\Phi(-d_2) - S_t e^{-q\tau}\Phi(-d_1) \approx e^{-r\tau} K\Phi(-d_2) $$
입니다.
일반적인 상황에서 무위험이자율 $r$은 양수죠. 이 때,
$$ e^{-r\tau} \Phi(-d_2) < 1$$입니다.
따라서
$$ p(t,S_t) < K \tag{1}$$
입니다. 내재가치인 $\max(K-S_t, 0)$ 은 $S_t \rightarrow 0$일 때 당연히
$$ \max(K-S_t , 0) \rightarrow K \tag{2}$$
이죠. 따라서 식(1)과 (2)에서
$$ p(t,S_t) < \max(K-S_t,0) ~~ \text{as} S_t \rightarrow 0$$
이 성립합니다.
이색적인 상황: 무위험 이자율이 양수가 아닐 때,
무위험 이자율이 제로금리 거나 2010년 후반대 유럽처럼 음의 금리를 가지다고 해 봅시다. 이 때는 상황이 좀 다릅니다.
만일 이자율 금리 $r=0$이면, 아래 그림처럼 됩니다(위의 코드에서 rfr 변수에 0을 넣어 실행하면 됨)
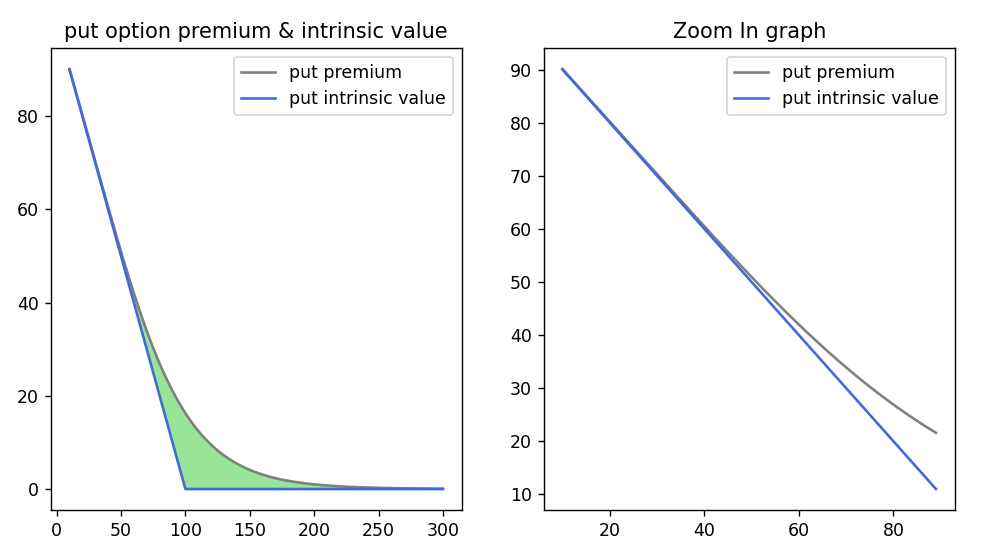
기초자산이 0이 되면 put 프리미엄과 내재가치가 딱 달라붙긴 하지만, 역전은 일어나지 않습니다. 더욱 드라마틱한 결과를 보기 위해 무위험 이자율을 -10%라 해볼까요?
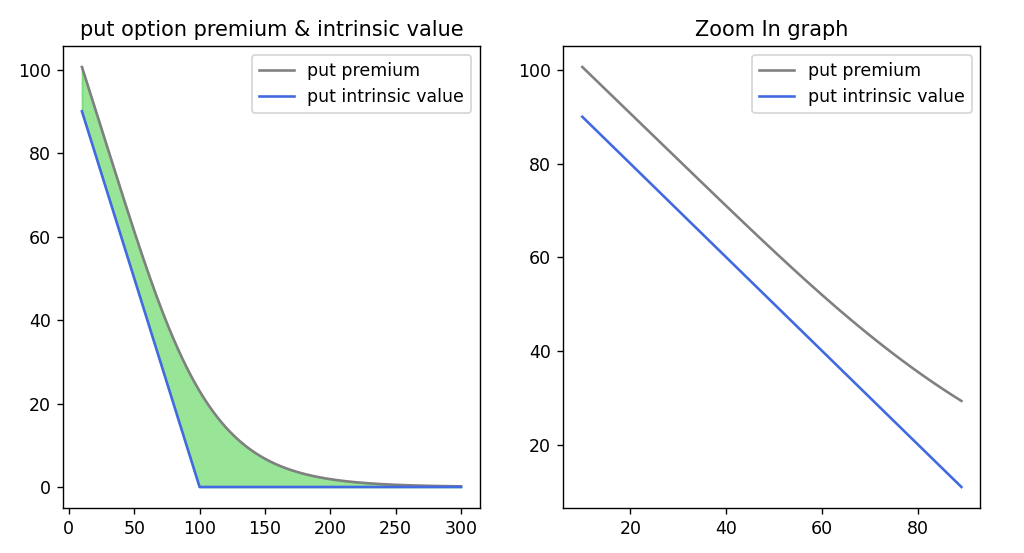
콜옵션의 경우처럼 put 프리미엄이 내재가치 보다 항상 위에 떠 있게 되죠.
따라서 결론을 내리면,
무위험 이자율이 양수인 상황에서 Deep ITM상황의 풋옵션의 프리미엄은 내재가치보다 작다
로 설명할 수 있겠습니다.
'금융공학' 카테고리의 다른 글
| 배당 없는 주식을 살 권리는 아메리칸 스타일이 곧 유로피안 스타일! (0) | 2023.01.05 |
|---|---|
| 옵션 시간가치 쩌는 곳은? (2) | 2023.01.03 |
| 옵션, 시간은 내편!: 시간가치와 내재가치 (0) | 2022.12.30 |
| 아메리칸 옵션의 평가 #3 : 함축적(implicit) FDM (0) | 2022.12.28 |
| 아메리칸 옵션의 평가 #2 : 이항트리 (0) | 2022.12.28 |




댓글