이 글에서는 European 콜/풋 옵션의 가격, 즉 프리미엄(premium)에 대한 여러가지 사실을 알아보도록 하겠습니다.
European 옵션의 경우 Black Scholes formula라는 수식이 존재했었죠. 옵션 #2. 옵션 프리미엄 구하기(Closed form) 글을 참고해 보시기 바랍니다.
콜옵션의 내재가치와 시간가치
간단한 관찰로, 콜옵션이나 풋옵션이나 미래 특정 시점(만기)의 기초자산 가격에 대한 권리를 행사하는 상품이기에 옵션의 가격은 음수가 될수 없습니다. 물론 0도 아니죠. 예컨대, European call option의 경우 closed form에 의한 그래프는 아래와 같이 됩니다.

(※ 행사가 100, 만기 1년, 기초자산 변동성 40%, 무위험 이자율 2%, 기초자산 연속배당율 1% 를 가정함)
위 가정하에서 기초자산이 20에서 150까지 움직일때의 가격 변화를 그려본 것입니다. 만일, 이 옵션이 바로 권리 행사된다고 가정하면 어떤 그래프를 그릴까요? 권리 행사때의 손익은, 기초자산의 가격이 $S$, 행사가를 $K$라 했을 때,
$$\max(S-K,0)$$
입니다. 위 그래프를 그려보면,
위와 같이 됩니다. 그림1과 그림2를 한 판에 그려 보면,

와 같이 됩니다. 콜옵션 그래프와 $\max(S-K,0)$ 식 사이의 영역을 강조해서 표현해 보겠습니다.
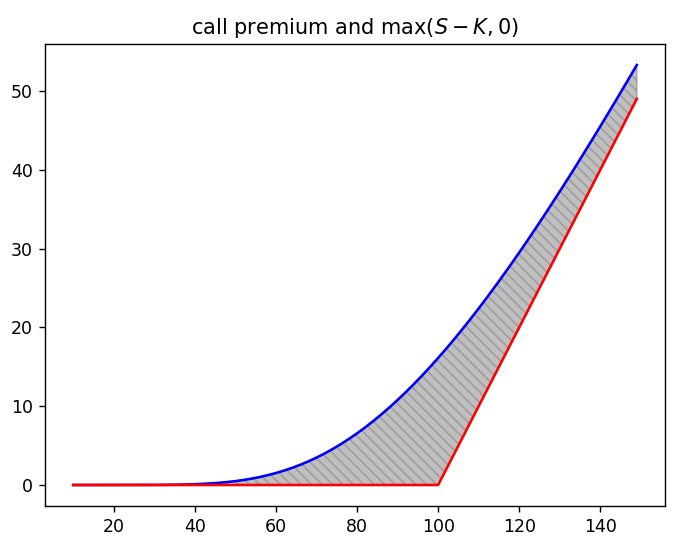
바로 권리를 행사했을 때 얻는 수익보다 콜옵션 프리미엄이 위로 더 올라와 있죠? 위 그림의 회색 영역만큼 값어치를 더 쳐준다는 얘깁니다. 특히 행사가인 100 보다 작은 구간에서는 권리 행사하면 수익이 0인데, 프리미엄은 통통히 살아나고 있습니다.
왜 그럴까요? 그 이유는 바로
만기까지 시간이 남았으니 그동안 주가가 오를 수도 있기 때문
입니다. 지금 당장 권리 행사가 안되는, 행사가 밑의 주가수준이더라도 만기까지 남은 기간 주가가 올라 수익를 얻을 확률이 있기 때문입니다.
이것을 우리는 시간 가치(time premium)라고 부릅니다. 만기까지 시간이 남아 있기에 기대해 봄직한 값인거죠. 바로 위 그래프의 회색 영역입니다.
바로 권리를 행사했을 때 얻는 수익 $\max(S-K,0)$에도 멋있는 이름이 있습니다. 바로 내재 가치(intrinsic value)입니다.
부연 설명을 하자면, 이 내재 가치에 따라 옵션의 상태를 3가지 유형으로 부릅니다.
| 구분 | 내용 |
| ITM (In The Money, 내가격) |
바로 권리 행사했을 때, 또는 청산했을 때 수익인 상태 |
| ATM (At The Money, 등가격) |
ITM과 OTM 사이의 상태, 주가의 미묘한 변화에 의해 수익 발생여부가 예민하게 결정되는 지지점 |
| OTM (Out of The Money, 외가격) |
바로 권리 행사했을 때, 또는 청산했을 때 수익이 없거나 손실인 상태 |
위 3가지 상태를 통틀어 머니니스(Moneyness)라 부릅니다.
그래프에 표시하면 아래와 같이 구분이 되죠.

결론적으로 콜옵션의 가치는 바로 권리행사할 때의 수익인 내재가치에 시간이 주는 혜택인 시간가치를 더하여 결정이 되는 것입니다. 아무리 내재 가치가 0인 지점이라도
남은 시간 동안 OTM이 ITM 상태로 전환될 기대감으로 콜옵션 프리미엄은 항상 양수
인 것이죠. 또한 콜옵션의 가격은
콜옵션 가치(프리미엄) = 내재가치 + 시간가치
로 표현이 됩니다.
내재가치야 주가와 페이오프 구조에 따라 결정된 값이라 뭐 따져볼게 없지만, 시간 가치는 어떤 특징을 가질까요?
당연히 남은 시간이 줄어들수록, 시간 가치는 작아지게 되겠죠. 기초자산이 변하여 OTM이었던 것이 ITM이 될 가능성이 점차 작아지게 됩니다.
만기가 줄어들면 시간가치는 어떻게?

남은 시간이 촉박하면 될 것도 안됩니다. python code를 통해 알아보도록 하죠.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
N = norm.cdf
def CallOptionBS(S, K, T, r, q, sigma):
if T == 0:
return np.max(S - K, 0)
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
return S * np.exp(-q * T) * N(d1) - K * np.exp(-r * T) * N(d2)
def option_and_intrinsic_value():
s0 = 100
strike = 100
rfr = 0.02
vol = 0.4
div = 0.01
mat_vec = [1 / 12, 1 / 2, 1, 3, 5]
s_vec = np.arange(10, 150, 1)
for i in range(5):
call_value = np.array([CallOptionBS(s, strike, mat_vec[i], rfr, div, vol) for s in s_vec])
plt.plot(s_vec, call_value, label='maturity {:.2f}'.format(mat_vec[i]))
call_intrinsic_value = np.maximum(s_vec - strike, 0)
plt.plot(s_vec, call_intrinsic_value, color='black', label='intrinsic value')
plt.title('call price and maturity')
plt.legend()
plt.show()
if __name__ == '__main__':
option_and_intrinsic_value()
code는 자주 설명했던 단순한 것으로서 여기서의 설명은 생략합니다. 결과를 보면,

위 그래프는 만기 1M, 6M, 1Y, 3Y, 5Y 이고 나머지 조건은 동일한 옵션의 그래프입니다. 제일 밑의 검은색 꺾인선은 내재가치(instrinsic value)입니다.
잔존만기가 크면 내재가치와의 차이가 크죠. 그만큼 시간가치가 높다는 뜻입니다. 만기가 1M까지 줄어들수록 내재가치에 딱 달라붙는 방향으로 옵션가격이 작아집니다. 그만큼 시간가치(time premium)이 사라지고 있다는 뜻이 되죠.
즉 같은 조건하에서는 만기가 긴 옵션이 만기가 짧은 옵션보다 비싸지게 됩니다.
내재가치는 똑같은데 시간가치가 늘어나니까요.
풋옵션은 어떨까?
풋옵션도 콜옵션과 비슷합니다. 만기가 남아 있으면, OTM 상태였던 것이 ITM 상태로 갈 수 있으니 그 기대에 의해 시간가치가 발생하죠. 하지만 콜옵션이랑 좀 다른 부분이 있습니다. 결론을 먼저 말하면 시간가치가 음수인, 즉 괜히 시간이 남아 있어서 손해보는 경우가 있다는 것이죠.
다음 글에서 명확히 알아보겠습니다.
'금융공학' 카테고리의 다른 글
| 옵션 시간가치 쩌는 곳은? (2) | 2023.01.03 |
|---|---|
| 풋옵션 시간가치의 비밀 (0) | 2023.01.02 |
| 아메리칸 옵션의 평가 #3 : 함축적(implicit) FDM (0) | 2022.12.28 |
| 아메리칸 옵션의 평가 #2 : 이항트리 (0) | 2022.12.28 |
| 아메리칸 옵션의 평가 #1 (이론) (0) | 2022.12.27 |




댓글