이 글은 아메리칸 옵션에 대한 설명
2022.12.27 - [금융공학] - 아메리칸 옵션의 평가 #1 (이론)
아메리칸 옵션의 평가 #1 (이론)
이번 글부터 몇 회에 걸쳐 아메리칸 옵션(American option)의 가격 계산에 대해 알아보도록 할까 합니다. 아메리칸 옵션에 대한 소개는 [금융공학] - 옵션에도 아메리칸 스타일이 있다 옵션에도 아메
sine-qua-none.tistory.com
에서 이어집니다.
저번 글에서 아메리칸 옵션의 연속가치(continuation value)와 행사가치(exercise value)에 대해서 설명하였고, 행사가치가 연속가치보다 클 때 행사가치로 치환하여 아메리칸 옵션의 가치를 계산할 수 있다고 했습니다.
풋옵션을 예로 들어 설명해 보겠습니다.
복습 | 유로피안 풋옵션의 계산(이항트리) python code
예전 글에서 콜옵션의 closed form과 이항트리 방법을 코딩하여 비교한 적이 있습니다. 보다 많은 상품을 다뤄보기 위해 풋옵션을 대상으로 하겠습니다.
풋옵션의 closed form은 여기를 참고하시면 됩니다.
아래 코드는 유로피언 풋옵션의 closed form과 이항트리를 이용한 가격 산출 code입니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import time
N = norm.cdf # cdf of standard normal random variable
def PutOptionBS(S, K, T, r, q, sigma):
if T == 0:
return np.max(K - S, 0) # 만기 payoff
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
return -S * np.exp(-q * T) * N(-d1) + K * np.exp(-r * T) * N(-d2)
# put의 closed form
def PutOption_BinomialTree(s0, strike, maturity, rfr, div, vol):
nNode = 200
dt = maturity / nNode
u = np.exp(vol * np.sqrt(dt)) # 기초자산 상승 비율
d = 1 / u
a = np.exp((rfr - div) * dt)
p = (a - d) / (u - d) # 기초자산 상승 확률
valueNode = np.zeros((nNode + 1, nNode + 1))
for n in reversed(range(nNode + 1)):
for i in range(n + 1):
spotS = s0 * u ** i * d ** (n - i) # 이항모형 주가 생성
if n == nNode: # 만기시,
valueNode[n, i] = max(strike - spotS, 0) # put 만기 payoff 대입
else:
up_val = valueNode[n + 1, i + 1]
down_val = valueNode[n + 1, i]
df = np.exp(-rfr * dt) # 할인 팩터
valueNode[n, i] = (p * up_val + (1 - p) * down_val) * df
# recursive formula
return valueNode[0, 0] # 시점 0, 현재가에서의 노드 값 return
def Calculate_put_option_closedform_bt():
s0 = 100
strike = 100
maturity = 1
rfr = 0.02
vol = 0.4
div = 0.01
s_vec = np.arange(10, 151, 10) # 10~150까지 10단위로 기초자산 벡터 세팅
# 151로 한 이유는 150을 포함시키기 위함
exact_value = np.array([PutOptionBS(s, strike, maturity, rfr, div, vol) for s in s_vec])
# 각 기초자산 레벨 별 closed form
bt_value = np.array([PutOption_BinomialTree(s, strike, maturity, rfr, div, vol) for s in s_vec])
# 각 기초자산 레벨 별 binomial tree 값
plt.plot(s_vec, exact_value, color='gray', marker='*', markersize=10, label='closed_form')
# binom. tree값과 비교를 위해 markersize를 키움
plt.plot(s_vec, bt_value, color='orange', marker='s', label='binomial tree')
min_difference_bt = min(bt_value - exact_value)
# closed form과 binom.tree 계산결과값 차이비교
print('Min difference between B.T and CLosedForm value : {:.3f}'.format(min_difference_bt))
plt.legend()
plt.show()
if __name__ == '__main__':
Calculate_put_option_closedform_bt()
코드는 예전 글에서 설명했던 것과 거의 똑같은 방법으로 작성됐습니다. 그 외 필요한 설명은 주석으로 갈음하겠습니다.
결과은 아래와 같습니다.
Min difference between B.T and CLosedForm value : -0.020

closed form 가격과 이항트리 가격이 아주 일치하고 있는 것이 확인됩니다(그림 사이즈를 키우면 closed form 결과를 의미하는 회색 별빛 marker가 뒤에 겹쳐 있는 것이 보일 것입니다.)
아메리칸 풋옵션의 계산
위의 풋옵션 이항트리 코드를 아주 살짝 변형하여 American Put을 계산할 수 있습니다. 아래를 보시죠.
def American_PutOption_BinomialTree(s0, strike, maturity, rfr, div, vol):
nNode = 200
dt = maturity / nNode
u = np.exp(vol * np.sqrt(dt))
d = 1 / u
a = np.exp((rfr - div) * dt)
p = (a - d) / (u - d)
valueNode = np.zeros((nNode + 1, nNode + 1))
for n in reversed(range(nNode + 1)):
for i in range(n + 1):
spotS = s0 * u ** i * d ** (n - i)
if n == nNode:
valueNode[n, i] = max(strike - spotS, 0)
else:
up_val = valueNode[n + 1, i + 1]
down_val = valueNode[n + 1, i]
df = np.exp(-rfr * dt)
conti_val, exer_val = (p * up_val + (1 - p) * down_val) * df, max(strike - spotS, 0)
valueNode[n, i] = max(conti_val, exer_val)
return valueNode[0, 0]
위의 PutOption_BinomialTree 함수와 완전 유사한데, 결정적인 차이를 보이는 부분이 있습니다. 바로 밑에서 2,3번째 줄인
conti_val, exer_val = (p * up_val + (1 - p) * down_val) * df, max(strike - spotS, 0)
valueNode[n, i] = max(conti_val, exer_val)부분입니다.
continuous value 부분과 exercise value를 각각 계산하여, 큰 값을 노드값으로 저장해 주는 것입니다! 이렇게 하는 이유는
아메리칸 옵션의 평가 #1 (이론) 에서 자세히 설명했습니다.
결과를 보기 위해
def Calculate_put_option_closedform_bt():
.....
bt_value = np.array([American_PutOption_BinomialTree(s, strike, maturity, rfr, div, vol) for s in s_vec])
.....
if __name__ == '__main__':
Calculate_put_option_closedform_bt()위와 같이 함수명만 바꿔 실행하면,
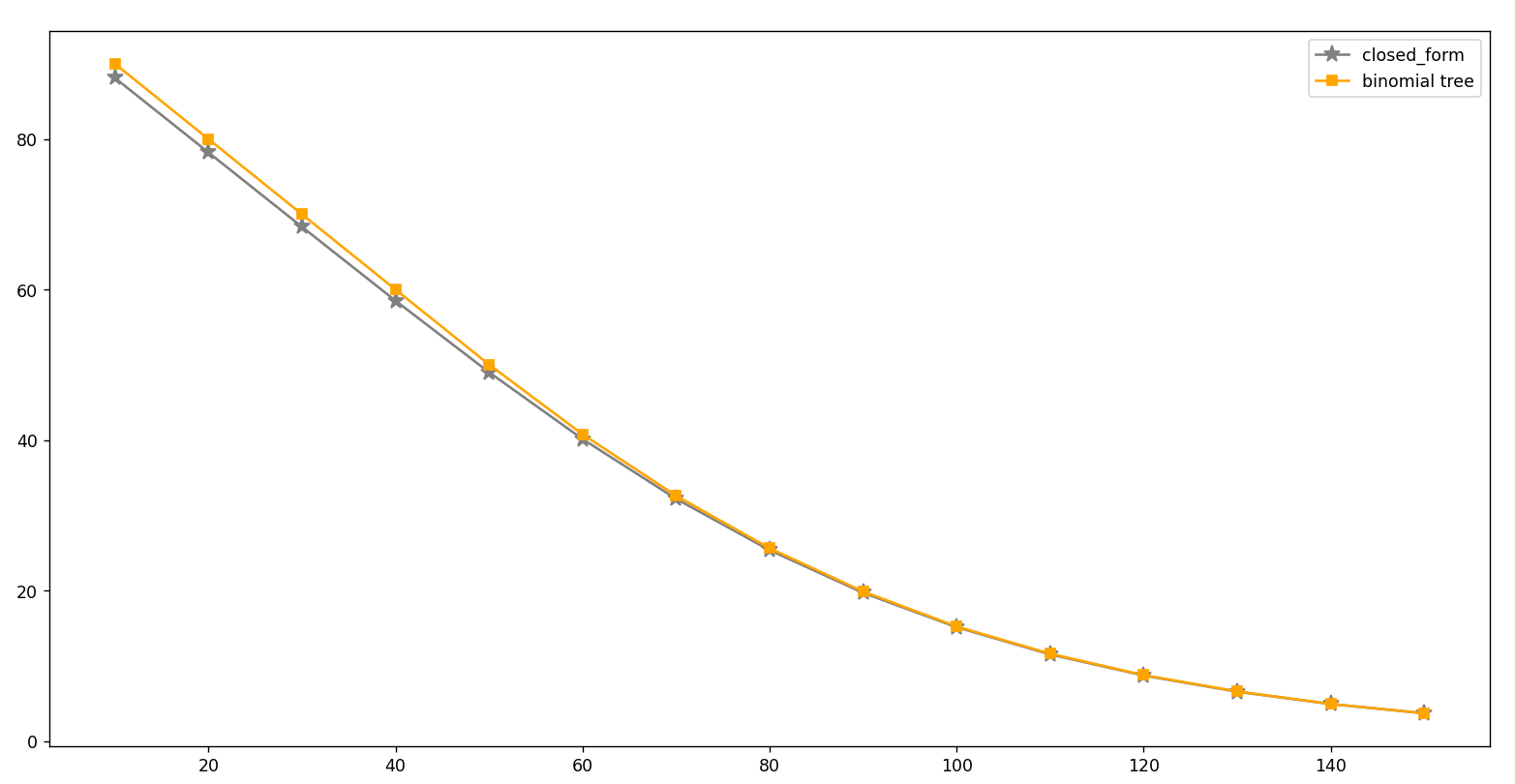
위와 같이 됩니다. 제일 위의 European put은 closed form 결과와 그래프가 겹칠 정도로 똑같았었는데요, American put은 차이가 나는 게 보이시죠?
이처럼 행사가치가 매 순간순간 time 노드마다 반영되어 연속가치와 비교되며 계산되므로 옵션 프리미엄이 상승하게 되는 것입니다. 이러한 계산법은 FDM 방법에서도 사용할 수 있습니다.
다음 글에서 계산해 보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 옵션, 시간은 내편!: 시간가치와 내재가치 (0) | 2022.12.30 |
|---|---|
| 아메리칸 옵션의 평가 #3 : 함축적(implicit) FDM (0) | 2022.12.28 |
| 아메리칸 옵션의 평가 #1 (이론) (0) | 2022.12.27 |
| 옵션에도 아메리칸 스타일이 있다 (0) | 2022.12.27 |
| 1star 스텝다운 ELS의 계산(Binomial Tree) #2 (0) | 2022.12.22 |




댓글