이번 글부터 몇 회에 걸쳐 아메리칸 옵션(American option)의 가격 계산에 대해 알아보도록 할까 합니다.
아메리칸 옵션에 대한 소개는 [금융공학] - 옵션에도 아메리칸 스타일이 있다
옵션에도 아메리칸 스타일이 있다
파생상품 중 가장 유명한 것은 아무래도 옵션(option)이겠죠. 기초자산을 살 권리(call option)를 매수/매도할 수도 있고 기초자산을 팔 권리(put option)를 매수/매도할 수 있습니다. 자세한 내용은 2022.0
sine-qua-none.tistory.com
을 참고하시기 바랍니다.
아메리칸 옵션은 옵션 만기 시점 전까지 아무 때나 권리를 행사할 수 있습니다. 따라서 일반 유로피언 플레인 바닐라 옵션(European Plain Vanilla option)에 비해 권리 행사 기회를 많이 주므로 그 값어치가 비싸겠죠(물론 투자자가 권리 행사를 엉뚱하게 하면 최악의 경우가 발생할 수도 있지만, 옵션을 만드는 사람 입장에서는 투자자가 항상 최적의 타이밍에 권리를 행사함을 가정하고 가치를 평가해야겠죠.)
문제는 언제 발생할지 모르는 행사 시점을 옵션 가치 평가에 어떻게 녹일 것이냐입니다.
행사가치와 연속가치
1. 현재시점(t=0) 에서부터 옵션 만기시점(T)까지 아메리칸 옵션의 가치가 있을 것입니다. 중간에 임의의 시점 t에서도 이 아메리카 옵션에서 기대할 수 있는 가치가 있겠죠. 당장 권리 행사를 하지 않았을 때 미래에 해당 옵션에서 기대될 가치 말입니다.
2. 반면에 지금 권리 행사를 해 버리는 것이 득인 경우도 있습니다. 미래의 가치를 보아하니 지금 행사하는 것보다 더 값어치가 없다고 판단될 때가 있겠죠. 이때는 그 순간 행사를 하여 이득을 취하는 것이 효율적입니다.
지금 당장 권리 행사를 했을 때, 나에게 떨어지는 이득을 행사가치(exercise value)라 합니다. 반면에 행사를 하지 않고 미래에 발생될 이득의 기댓값은 연속가치(continuation value)라 합니다.
아메리칸 옵션을 가진 투자자는 이 두 개의 가치 (행사가치, 연속가치)를 시시각각 비교해 보며, 어떤 가치가 더 큰지를 계속 판단하게 됩니다. 이 때 두 가지의 가능성이 존재하겠죠.
| 구분 | 액션 |
| 연속가치 > 행사가치 | 바로 권리 행사하지 않고 향후 기초자산 움직임을 지켜보기 |
| 연속가치 < 행사가치 | 당장 행사하고 옵션 끝내기 |

행사가치(Exercise Value)
행사가치는 쉽습니다. 임의의 시점 t에서 기초자산의 가격이 St일 때, 행사가가 K인 옵션에 대해서 행사가치는
| 콜옵션 | 풋옵션 |
| max | \max(K-S_t,0) |
이 되죠. 연속가치는 어떻게 될까요?
연속가치
연속가치는 바로 행사하지 않고 보유했을 때의 가치, 즉 해당 옵션의 잔존 만기 동안의 수익의 기댓값입니다.
만일 유러피언이면 Black Scholes formula 같은 수학 공식도 있고 그럴 텐데, 머지않은 미래에 또 권리 행사 타이밍이 발생할지도 모르죠. 비록 당장은 안 하더라도 말입니다. 그래서 얘는 미래에서부터 당겨와야 합니다.
옵션의 가장 먼 미래는 바로 옵션의 만기죠. 옵션 만기 시에는 무조건 페이오프가 결정되어 있습니다. 여기서부터 backwardation으로 가치를 할인해 와야 합니다.
파생상품을 평가하는 방법론 중 backwardation으로 미래가치를 차츰차츰 당겨오는 방법론이 두 가지가 있었습니다. 바로
함축적 FDM 방법, 이항트리
였죠 (MonteCarlo Simulation에서도 미래가치를 당겨오는 방법으로 연속가치를 구할 수 있습니다. 이것은 차후에 설명하겠습니다.)
아메리칸 옵션의 평가 방법론
연속가치를 구하기 위해 미래의 페이오프를 차츰차츰 backward로 당겨오는 방법을 써야 하고, 이를 구현하기 쉬운 방법은 바로 함축적(implicit) FDM방법과 이항트리 방법입니다. 간단히 방법론을 살펴보죠.
함축적 FDM 방법
격자판을 보시죠. 풋옵션 기준으로 설명하겠습니다.

이제 만기에서 하루전날 연속가치를 구해볼까요?

바로 왼쪽 열인 만기 하루전날의 격자점의 값을 구할 수 있습니다(붉은 영역.) 이게 바로 시점 T-1에서의 연속가치입니다.
이다음이 중요합니다!
이 옵션은 아메리칸 옵션이므로 이 연속가치와 행사가치의 크기를 비교해줘야 합니다, 만일 행사가치가 큰 격자점이라면 행사가치로 바꿔줘야겠지요.
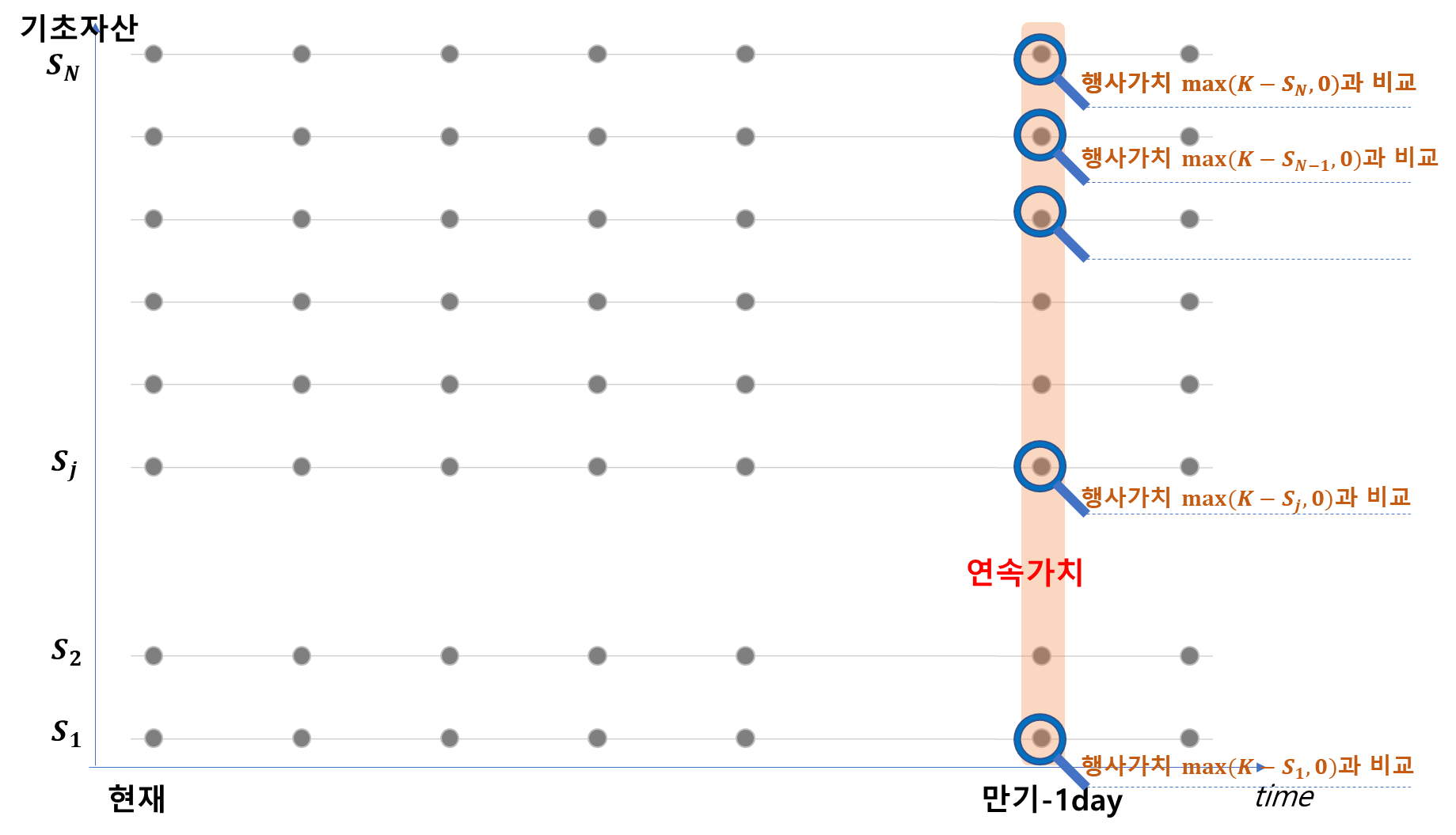
궁극적으로
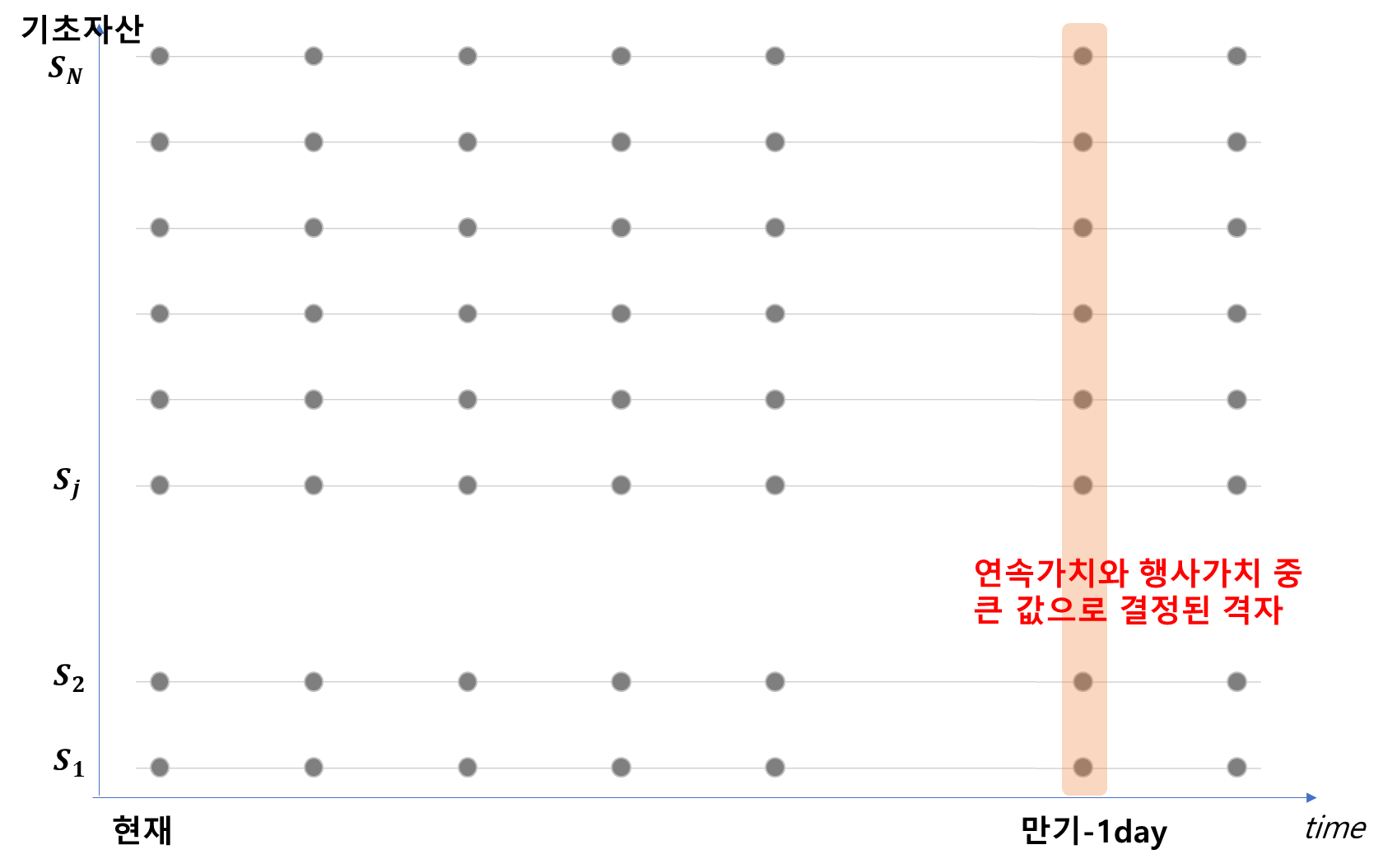
위와 같이 업데이트가 됩니다.
위 내용을 현재시점 (제일 왼쪽 격자)까지 반복해 줍니다!
사실 내용은 좀 복잡해도, 코딩은 생각만큼 어렵지 않습니다. 한 줄 정도만 새롭게 추가해 주면 됩니다.
또 다른 backward 방법은 이항트리 방법을 보시겠습니다.
이항 트리
FDM 방법이 직사각형 모양의 격자라면, 이항트리는 세모꼴 노드라는 점만 다르지, 과정은 똑같습니다. 아래 세모 모양 트리를 보실까요?

이제 전단계인 N-1단계를 이항모형으로 풀어봅니다.
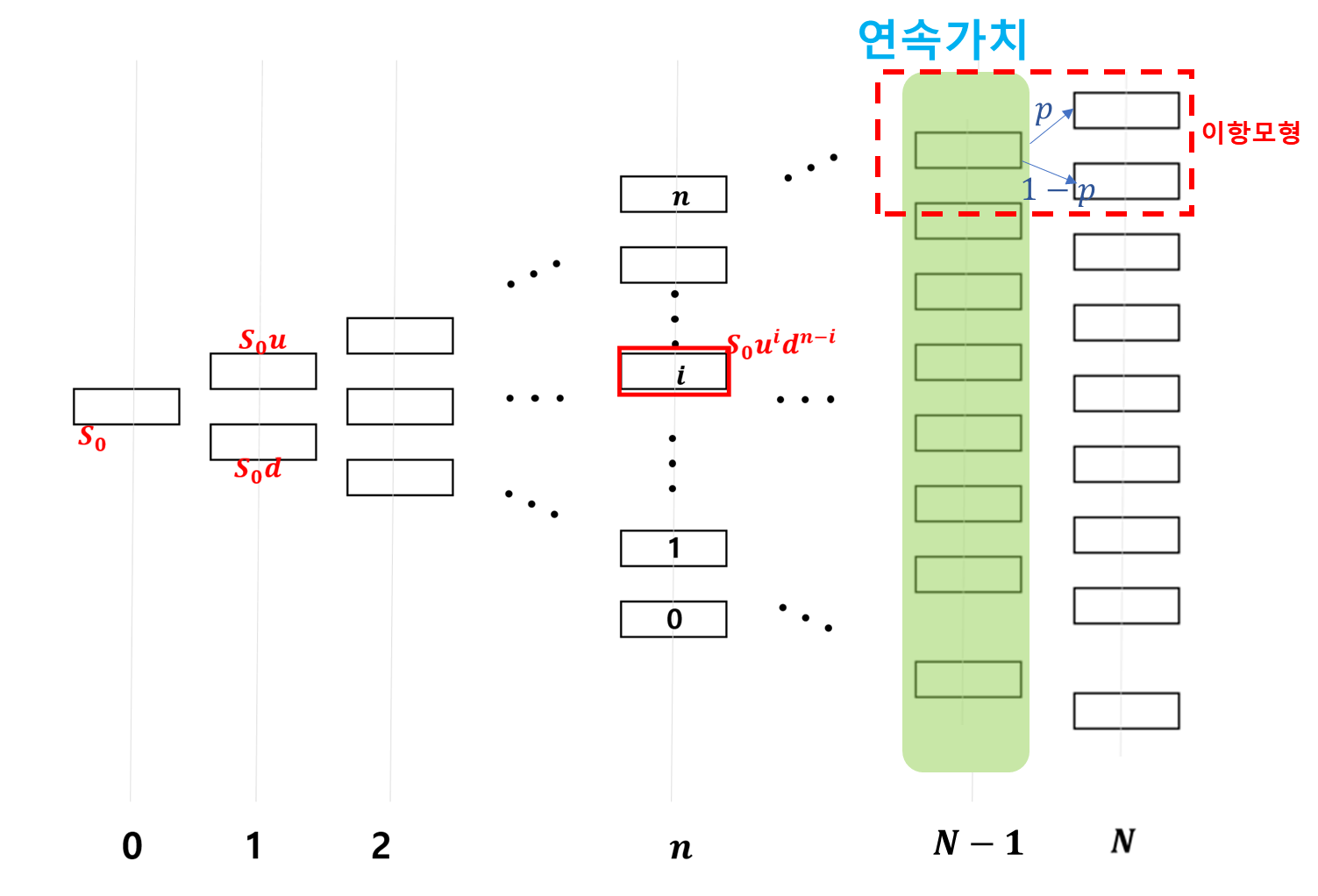

이런 식으로 업데이트되어서 N-1번째 타임의 노드들이 완성이 됩니다. 이것을 시점에 대해 backward로 0 단계까지 내려오는 것입니다.
이것 또한 설명은 복잡해 보이나, 코딩은 생각 외로 쉽습니다. 기존 이항트리 코드에 한 줄 정도만 추가해 주면 됩니다.
다음 글에서 직접 파이썬 코딩을 통해 아메리칸 옵션의 가격을 구해보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 아메리칸 옵션의 평가 #3 : 함축적(implicit) FDM (0) | 2022.12.28 |
|---|---|
| 아메리칸 옵션의 평가 #2 : 이항트리 (0) | 2022.12.28 |
| 옵션에도 아메리칸 스타일이 있다 (0) | 2022.12.27 |
| 1star 스텝다운 ELS의 계산(Binomial Tree) #2 (0) | 2022.12.22 |
| 1star 스텝다운 ELS의 계산(Binomial Tree) #1 (0) | 2022.12.21 |




댓글