이번 글은
2023.01.05 - [금융공학] - 배당 없는 주식을 살 권리는 아메리칸 스타일이 곧 유로피안 스타일!
배당 없는 주식을 살 권리는 아메리칸 스타일이 곧 유로피안 스타일!
이 글에서는 아메리칸 옵션(American option)의 재미있는 특징을 알아볼까 합니다. 이전의 글 아메리칸 옵션의 평가 #1 (이론), 아메리칸 옵션의 평가 #2 : 이항트리 아메리칸 옵션의 평가 #3 : 함축적(im
sine-qua-none.tistory.com
에서 다루었던 내용을 수학적으로 접근해 보도록 하겠습니다.
옵션의 가치를 이항트리 모형으로 계산한다고 하고 트리의 각 노드별로 연속가치가 어떻게 되는지를 살펴보겠습니다.
기초자산 가격이 S일 때, 옵션의 만기 페이오프를 f(S)라 정의합시다. 예를 들어 콜옵션의 경우는
f(S)=c(T,S)=max
이고 풋옵션의 경우는
f(S) = p(T,S) = \max(K-S,0)
입니다. 여기서T는 옵션의 만기, K는 행사가 입니다.
이항트리의 뒤에서부터 n번째 노드에서 기초자산 S일 때의 연속가치(continuation value)를 V_n(S)라 하죠.
예를 들어 아래 그림과 같이 3 단계 트리가 있을 경우 V_0, V_1, V_2, V_3는 아래의 연속가치를 뜻합니다.

연속가치(continuation value)의 계산
위에서 정의한 만기페이오프 f(S)를 이용하여, n단계 backward step의 연속가치 V_n(\cdot)를 표현해 보기로 합시다. 이항모형은 아래와 같습니다.

0 단계 backward step :V_0
0 단계는 만기시점이므로 연속가치 개념은 없지만 페이오프는 f 이기 때문에 V_0는
V_0 (S) = f(S)
라 할 수 있습니다.
1단계 backward step : V_1
[그림 1] 이항모델에 의해 임의의 S에 대해
V_1(S) = d\cdot \left[ p f(Su) + (1-p)f(Sd) \right]\tag{1}
입니다. 여기서 d는 한 단계 할인팩터로서, d:=e^{-r\Delta t}입니다.
2단계 backward step : V_2

2단계는 위와 같은 그림일 겁니다. V_2(S)는
V_2(S) = d \left[ p V_1(Su) + (1-p)V_1(Sd) \right]
입니다. 그런데 V_1(\cdot)는 식(1)에서 구해놓았죠, 따라서 계산하면,
\begin{align} V_2(S) &= d [ p V_1(Su) +(1-p) V_1(Sd)]\\ & = d[ p[ d( pf(Su^2)+(1-p)f(Sud) )] + (1-p)[ d( pf(Sdu)+(1-p)f(Sd^2) )]]\\ & = d^2 \left[ p^2f(Su^2) + 2p(1-p)f(S) +(1-p)^2 f(Sd^2) \right]\\ & =d^2 \sum_{i=0}^2 {}_2 C_i p^i (1-p)^{2-i} f (Su^i d^{2-i})\tag{2} \end{align}
와 같이 됩니다. 어쩐지 이항전개 느낌이 나는군요. 계속 보겠습니다.
n단계 backward step : V_n
식(1)과 식(2)를 보니 왠지 V_n은
V_n(S) = d^n \sum_{i=0}^n {}_n C_i p^i (1-p)^{n-i} f (Su^i d^{n-i}) \tag{3}
일 듯합니다. 이는 수학적 귀납법(induction)으로 증명이 가능합니다. 증명은 아래 더보기를 클릭해 보시죠.
n=2일 때는 식(2)에서 보였습니다. 이제 V_n이 식(3)이라 가정하고 V_{n+1}이 같은 모양이 나오는지 보면 됩니다.
\begin{align} V_{n+1}(S) &= d\left[ pV_n(Su) + (1-p) V_n (Sd) \right] \\ &= d^{n+1}\left[ p\sum_{i=0}^n {}_n C_i p^i (1-p)^{n-i} f (Su^{i+1} d^{n-i}) + (1-p) \sum_{j=0}^n {}_n C_j p^j (1-p)^{n-j} f (Su^j d^{(n+1)-j}) \right] \\ &= d^{n+1}\left[ \sum_{i=0}^n {}_n C_i p^{i+1} (1-p)^{n-i} f (Su^{i+1} d^{n-i}) + \sum_{j=0}^n {}_n C_j p^j (1-p)^{(n+1)-j} f (Su^j d^{(n+1)-j}) \right] \\ &~~~(k=i+1)\\ & =d^{n+1}\left[ \sum_{k=1}^{n+1} {}_n C_{k-1} p^{k} (1-p)^{(n+1)-k} f (Su^{k} d^{(n+1)-k}) + \sum_{j=0}^n {}_n C_j p^j (1-p)^{(n+1)-j} f (Su^j d^{(n+1)-j}) \right] \\ &~~~(k=j) \\ & =d^{n+1}\left[ \sum_{j=1}^{n+1} {}_n C_{j-1} p^{j} (1-p)^{(n+1)-j} f (Su^{j} d^{(n+1)-j}) + \sum_{j=0}^n {}_n C_j p^j (1-p)^{(n+1)-j} f (Su^j d^{(n+1)-j}) \right] \\ & =d^{n+1}\left[ \sum_{j=1}^n ( {}_n C_{j-1}+{}_n C_j) p^{j} (1-p)^{(n+1)-j} f (Su^{j} d^{(n+1)-j}) + {}_n C_n p^{n+1}f(Su^{n+1}) + {}_n C_0 (1-p)^{n+1}f(Sd^{n+1}) \right] \\ & =d^{n+1}\left[ \sum_{j=1}^n {}_{n+1} C_{j} p^{j} (1-p)^{(n+1)-j} f (Su^{j} d^{(n+1)-j}) + {}_n C_n p^{n+1}f(Su^{n+1}) + {}_n C_0 (1-p)^{n+1}f(Sd^{n+1}) \right] \\ & =d^{n+1}\left[ \sum_{j=0}^{n+1} {}_{n+1} C_{j} p^{j} (1-p)^{(n+1)-j} f (Su^{j} d^{(n+1)-j})\right] \\ \end{align}
이렇게 증명할 수 있습니다.
결론
위의 관찰을 종합하면 다음의 결론을 얻을 수 있습니다.
이항트리에서 구한 현재가 공식
time step이 모두 N개인 이항트리 안에서, 만기 페이오프가 f인 상품의 현재가치는
d^N \sum_{i=0}^N {}_N C_i p^i (1-p)^{N-i} f (Su^i d^{N-i}) \tag{*}
단 위의 식 (*)는 연속가치를 재귀적으로 할인해서 구한 현재가입니다.
아메리칸 옵션같이 행사가치와 비교해서 큰 값으로 치환하는 과정이 있으면 식(*)은 맞지 않게 됩니다.
자, 그럼 식(3)처럼 단계별 연속가치의 값을 알아냈으니 이제 행사가치와 비교해 볼까요? 연속가치와 행사가치 중 어떤 값이 더 큰지에 따라 아메리칸 옵션의 가격이 결정될 테니, 아메리칸 옵션의 비밀도 어느 정도 풀릴 것 같습니다.
그전에 수학적으로 아주 유명한 부등식 하나를 소개하겠습니다.
젠센부등식(Jensen's Inequality)
수학적으로 (아래로) 볼록한 볼록함수(convex function)의 정의는 아래와 같습니다.
| 볼록함수(convex) |
| 함수 f:D\rightarrow \mathbb{R}가 볼록함수라는 것은 임의의 x,y\in D와 0\leq t\leq 1인 실수 t에 대해 f(tx+(1-t)y) \leq tf(x) +(1-t)f(y) 를 만족하는 함수이다. |
위키피디아에 관련 그림이 있어 소개합니다. 그림으로 보면 아래와 같습니다.
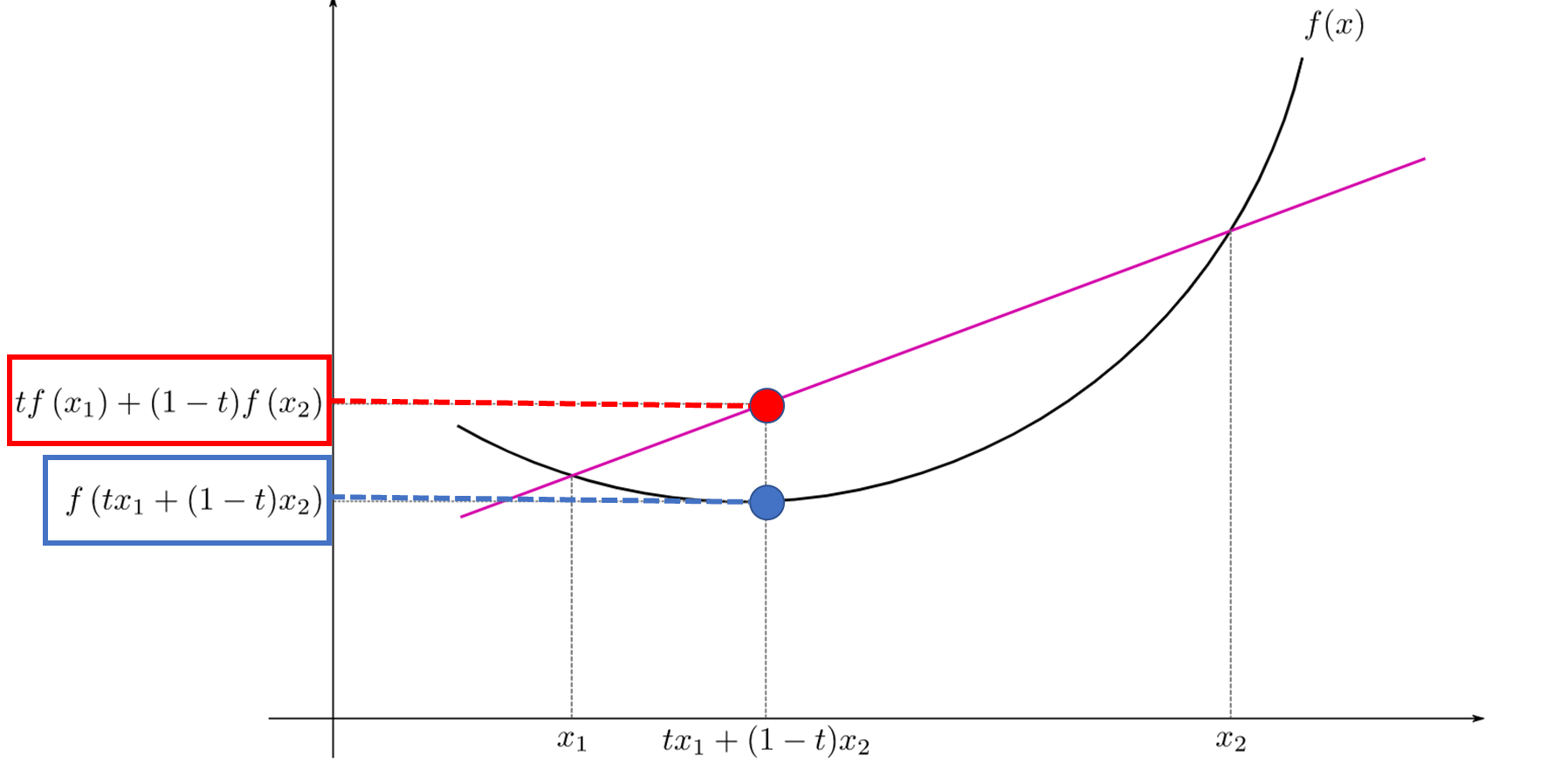
아래로 볼록하기 때문에 내분한 점의 함숫값이 함숫값의 내분점보다 작아지게 되는 것이죠.
여기서 중요한 부등식이 하나 등장하는데요. 바로 젠센 부등식입니다.
| 젠센부등식 |
| 일반적으로 0이 아닌 n개의 실수 \alpha_1,\alpha_2, \cdots , \alpha_n이 \sum_{i=1}^n \alpha_i =1 을 만족할 때, 임의의 실수 x_1, x_2,\cdots, x_n에 대해 f\left( \sum_{i=1}^n \alpha_i x_i \right) \leq \sum_{i=1}^n \alpha_i f(x_i) 성립한다. 즉, n개의 점이 있을 때, 이 점들의 가중평균의 함수값이 함숫값의 가중평균보다 작다는 뜻 |
이제 이 부등식을 이용하여 연속가치와 행사가치를 비교해 보겠습니다.
연속가치와 행사가치의 비교
앞선 이항트리에서 n번째 backward step에서 기초자산 주가를 S라 하면,
| 옵션의 연속가치 | V_n(S) |
| 옵션의 행사가치 | f(S) |
입니다. 이해를 돕기 위해, 고정된 n과 0\leq i\leq n에 대해
\alpha_i = {}_n C_i p^i(1-p)^{n-i}
라 하면 이항전개에 의해
\sum_{i=0}^n \alpha_i = (p+(1-p))^n = 1
입니다. 즉 \alpha_i들은 가중평균에 쓰일 가중계수(weighted coefficient)라 볼 수 있죠. 그러면 젠센부등식에 의해
\begin{align} V_n(S) &= d^n \sum_{i=0}^n \alpha_i f (Su^i d^{n-i}) \\ & \geq d^n f\left( \sum_{i=0}^n \alpha_i Su^i d^{n-i} \right) \\ & =d^n f\left( \sum_{i=0}^n {}_n C_i p^i(1-p)^{n-i} Su^i d^{n-i} \right) \\ & =d^n f\left( \sum_{i=0}^n {}_n C_i S(pu)^i ((1-p)d)^{n-i} \right) \\ & = d^nf\left( S (pu + (1-p)d)^n \right) \\ & =d^n f\left( Se^{n(r-q)\Delta t} \right) \tag{5} \end{align}
가 성립합니다. 마지막 줄은 아래의 등식 때문에 만족합니다.
\begin{align} pu+(1-p)d &= (u-d)p + d\\ & = (u-d) \cdot \frac{e^{(r-q)\Delta t}-d}{u-d} +d\\ & = e^{(r-q)\Delta t} \end{align}
식(5)을 결과만 써보면,
V_n(S) \geq d^n f\left( Se^{n(r-q)\Delta t} \right) \tag{**}
입니다. 이것을 가지고 분석해 보죠.
콜옵션의 경우
콜옵션의 만기페이오프는 f(S) = \max(S-K,0) 이고 이것은 볼록함수입니다. 따라서
\begin{align} V_n(S) & \geq e^{-rn\Delta t} \max(Se^{n(r-q)\Delta t} -K,0)\\ & = \max(Se^{-nq\Delta t} -Ke^{-nr\Delta t}, 0) \end{align}
이때, 이자율 r이 음수가 아니고, 배당률 q=0이면,
V_n(S) \geq \max(S-K,0)
입니다.
즉 연속가치가 행사가치가 크므로 이항트리 각 노드에서 연속가치가 행사가치로 치환될 유인이 없는 거죠.
이 뜻은 즉, 이자율이 양수인 일반적인 상황에서라면,
연속배당률이 0이면 아메리칸 콜옵션과 유로피안 콜옵션은 가격이 같다
라는 결론입니다. 저번 글에서 봤던 내용과 똑같죠.
풋옵션의 경우
풋옵션의 만기페이오프 f(S) = \max(K-S,0) 이고 볼록함수입니다. 따라서
\begin{align} V_n(S) & \geq e^{-rn\Delta t} \max(K- Se^{n(r-q)\Delta t}, 0)\\ & = \max(Ke^{-nr\Delta t}- Se^{-nq\Delta t} , 0) \end{align}
따라서 q=0이고 Ke^{-nr\Delta t} >K 즉, r이 음수일 때,
V_n(S) \geq \max(K-S,0)
입니다. 어쨌든 r이 음수인 특별한 상황에서야 연속가치가 행사가치가 더 커서 두 값이 치환될 유인이 사라지는 거죠. 그런데 음의 이자율은 금융이론적으로는 매우 특수한 경우입니다. 그래서 다음의 결론을 얻습니다.
콜옵션과 달리, 풋옵션은 아메리칸 옵션이 유로피안 옵션보다 가치가 크다(다만, 이자율이 음수인 상황에서는 같아지는 경우도 있다(배당이 0일 때))
라 결론지을 수 있겠습니다.
'금융공학' 카테고리의 다른 글
| 여러개의 기초자산을 가지는 파생상품 가격결정식 (0) | 2023.01.13 |
|---|---|
| 풋옵션 시간가치가 없어지는 영역은? (0) | 2023.01.11 |
| 배당 없는 주식을 살 권리는 아메리칸 스타일이 곧 유로피안 스타일! (0) | 2023.01.05 |
| 옵션 시간가치 쩌는 곳은? (2) | 2023.01.03 |
| 풋옵션 시간가치의 비밀 (0) | 2023.01.02 |




댓글