이 글은
2022.07.19 - [금융공학] - GBM의 확장판들 #1. 기대수익률/변동성을 시간함수로!
GBM의 확장판들 #1. 기대수익률/변동성을 시간함수로!
2022.06.20 - [수학의 재미/확률분포] - Log Normal Distribution 이번 글은 2022.07.18 - [금융공학] - 위험중립측도와 market price of risk 위험중립측도와 market price of risk 이번 글은 2022.06.27 - [금융..
sine-qua-none.tistory.com
에서 이어집니다.
주가의 움직임에서 중요한 부분을 차지하는 것이 바로 배당입니다. 배당이 결정되면 그 배당금액만큼 주가가 떨어지는 현현상이 발생하죠.
보통 우리나라 거래소에 상장되어 있는 주식은 연말에 한번 년 배당을 합니다. 요즘은 주주친화적인 분위기에 힘입어 중간배당을 하는 상장사가 늘어나는 추세인데요. 삼성전자 등 약 60여 상장사에서 중간배당을 실시하는 것으로 알고 있습니다. 특히 삼성전자는 분기에 한 번씩 배당을 하는 분기배당 정책을 쓰고 있습니다.
이 글에서는
1. 간략히 삼성전자의 분기배당 내역들을 살펴보고
2. 배당을 주가 모델에 어떻게 반영하는지
알아보도록 하죠.
삼성전자 배당금 조회
삼성전자는 하나의 예시이고, 나머지 상장사에 대해서도 아래와 같은 방법으로 조회가 가능합니다.
1. 공시 사이트 접속
공시사이트에 접속하면 다음과 같은 창이 뜹니다.

2. 삼성전자 상세조건 검색으로 배당관련 공시 추출

이와 같이 하면, 기간은 오늘로부터 1년이 디폴트로 설정되고 다음의 결과가 나옵니다.

딱 분기배당 4건, 총 1년의 현금/현물 배당 결정 공시 결과가 잡힙니다.
하나하나씩 열어 살펴본 결과를 표로 정리해 보면
| 공시일 | 배당기준일 | 배당금액(원) | 기준일 종가(원) |
| 22.04.28 | 22.03.31 | 361 | 69,600 |
| 22.01.27 | 21.12.31 | 361 | 78,300 |
| 21.10.28 | 21.09.30 | 361 | 74,100 |
| 21.07.29 | 21.06.30 | 361 | 80,700 |
1년간, 배당을 1,444원(=361 × 4회) 주는 회사이군요.
정해진 날짜에 정해진 금액을 주는 이러한 배당을 금융공학적으로 이산 배당(discrete dividend)이라고 합니다.
그런데 모델링 측면에서 봤을 때, GBM 모델은 시간 t에 대한 연속적인 모델이죠.
따라서, 이 배당을 연속적으로 바꾸어 GBM 모델에 녹입니다.
삼성전자의 경우 1년에 1,444원을 주는데, 기준이 되는 주가를 21.06.30의 80,700이라 생각을 하는 것입니다. 그러면
배당률:=q=1,44480,700=1.79
라고 생각하는 것이죠. 즉 1년에 1.79%의 배당을 주는 주식이라 간주합니다.
주가 모델 GBM에 배당 반영
보통 금융공학에서 배당률을 q라는 기호로 많이 씁니다. 그러면 극히 짧은 순간 dt동안 배당락에 의해, 주가의 수익률 dSt/St은
−qdt
만큼 조정을 받게 됩니다. 삼성전자의 경우
q=1.79
인 거죠. 이런 상황에서, GBM 모델은 다음과 같이 업그레이드가 되죠.
dStSt=rdt+σdWt−qdt=(r−q)dt+σdWt
더욱더 확장하여, 지난 글 (2022.07.19 - [금융공학] - GBM의 확장판들 #1. 기대수익률/변동성을 시간함수로!)에서처럼 r,q,σ를 모두 시점 t에 대한 함수로 두면
dStSt=(r(t)−q(t))dt+σ(t)dWt
와 같이 쓸 수 있는 것입니다.
배당없는 주가 vs 이산배당 주가 vs 연속배당 주가 예시
그렇다면 배당을 고려하지 않는 주가에 이산 배당과 연속 배당을 적용했을 때, 주가의 움직임이 어떻게 되는지 코드를 통해 보죠.
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import scipy.stats as stats
def dividend_test():
s0 = 100
mu = 0.02
sigma = 0.2
T = 1
days = 250
dt = 1 / days
nSteps = T * days
zNormal = np.random.normal(size = nSteps + 1)
s_process = np.zeros(nSteps +1)
s_process[0] = s0
drift = (mu - 0.5 * sigma ** 2) * dt
diffusion = sigma * np.sqrt(dt)
cont_dividend = 0.1
cont_div_process = np.zeros(nSteps + 1)
cont_div_process[0] = s0
disc_dividend = s0 * cont_dividend
exdiv_date = 100
disc_div = np.zeros(nSteps + 1)
disc_div[exdiv_date:] = -disc_dividend
cont_div_drift = (mu - cont_dividend - 0.5 * sigma ** 2) * dt
for i in range(1, nSteps+1):
s_process[i] = s_process[i - 1] * np.exp(drift + diffusion * zNormal[i])
cont_div_process[i] = cont_div_process[i - 1] * np.exp(cont_div_drift + diffusion * zNormal[i])
disc_div_process = s_process + disc_div
print('terminal value of NO DIVIDEND PATH : {:.2f}'.format(s_process[-1]))
print('terminal value of Cont DIVIDEND PATH : {:.2f}'.format(cont_div_process[-1]))
print('terminal value of Disc DIVIDEND PATH : {:.2f}'.format(disc_div_process[-1]))
plt.plot(s_process, 'r', label='No dividend')
plt.plot(cont_div_process, 'b', label='Continuous dividend')
plt.plot(disc_div_process, 'y', label='Discrete dividend')
plt.vlines(nSteps,cont_div_process[-1],s_process[-1], colors='k', linestyles ="dashed")
plt.text(nSteps, np.mean([s_process[-1], cont_div_process[-1]]), round(cont_div_process[-1]-s_process[-1],2) )
plt.legend()
plt.show()
if __name__ == '__main__':
dividend_test()
간단히 코드를 살펴보겠습니다.
s0 = 100 # 현재주가
mu = 0.02 # 주가의 기대수익률, risk free rate라 생각해도 됨
sigma = 0.2 # 주가의 변동성 20% 가정
T = 1 # 만기 1년
days = 250
dt = 1 / days
nSteps = T * days #1년을 250일로 가정
zNormal = np.random.normal(size = nSteps + 1) # 일수에 맞춰 주가생성을 위한 normal random number 추출
s_process = np.zeros(nSteps +1) # 배당 고려안한 주가 path을 위한 배열
s_process[0] = s0 # 배열의 초기값은 s0로 둠
drift = (mu - 0.5 * sigma ** 2) * dt # 주가의 drift term
diffusion = sigma * np.sqrt(dt) # 주가의 diffusion term
cont_dividend = 0.1 # 연속배당률을 q=10%로 (과장되게, 눈에 잘보이도록)설정
cont_div_process = np.zeros(nSteps + 1) # 연속배당을 고려한 주가 process
cont_div_process[0] = s0 # 연속배당 주가 process의 초기값은 s0 로 설정
disc_dividend = s0 * cont_dividend # 이산배당은 1년에 딱 한번, s0*q 로 설정#
exdiv_date = 100 # 현재시점에서 100일 뒤 이산배당 발생
disc_div = np.zeros(nSteps + 1)
disc_div[exdiv_date:] = -disc_dividend # 100일 뒤부터 이산배당으로 인한 주가 조정분
cont_div_drift = (mu - cont_dividend - 0.5 * sigma ** 2) * dt #연속배당의 drift term (r-q-1/2σ^2)dt
for i in range(1, nSteps+1):
s_process[i] = s_process[i - 1] * np.exp(drift + diffusion * zNormal[i])
#배당 고려 안한 주가 process 추출
cont_div_process[i] = cont_div_process[i - 1] * np.exp(cont_div_drift + diffusion * zNormal[i])
#연속배당 고려한 주가 process 추출
disc_div_process = s_process + disc_div #배당없는 주가 path에 이산배당 조정분 고려한 path 추출
결과는 다음과 같습니다.
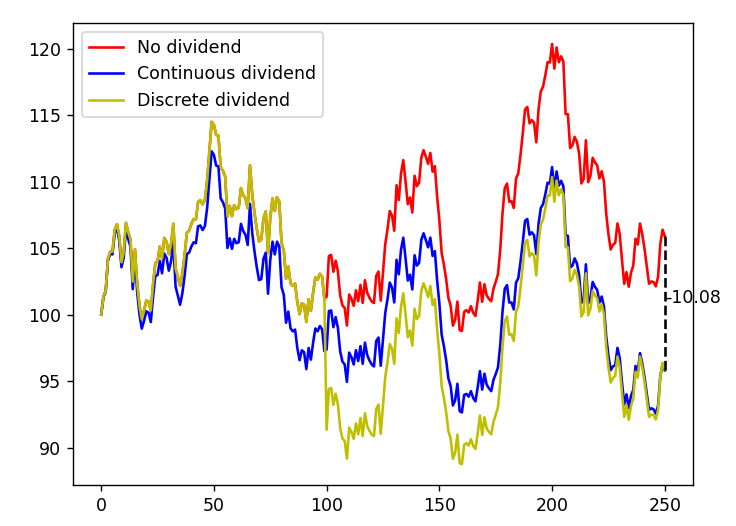
○ 노란색 주가(이산 배당)는 100일 정도에 크게 떨어지는 모습이 보입니다. 배당량만큼 주가가 조정이 되는 것이죠.
○ 반면, 파란색 주가(연속 배당)는 전 기간(250일)에 걸쳐 연속적으로 반영합니다. 끝에서는 노란색 선과 얼추 만나겠죠.
○ 노란, 파란색 주가와 빨간색 주가를 각각 비교해보면 250일 뒤 종가에 약 10 정도 차이 남을 볼 수 있습니다. code에서 설정한 q=10가 반영된 결과입니다.
배당의 효과가 분명 존재하기 때문에 GBM 모델에 배당을 반영해주는 것은 당연합니다. 하지만 이것을
○ 연속 배당으로 반영할지,
○ 이산 배당으로 반영할지
의 문제가 있습니다. 각각의 장, 단점이 있기에 상황과 계산 역량에 맞게 모델을 선택해서 사용하면 됩니다.
| 장점 | 단점 | |
| 연속배당 | GBM 모델의 drift 항만 r에서 r−q로 살짝 바꿔서 사용가능 | 정확한 배당 발생 시점과 배당량을 고려하지 않아 주가 움직임을 충분히 반영하지 못함 |
| 이산배당 | 배당락의 정확한 시점과 주가조정분을 적확하게 반영할 수 있음 | 계산이 복잡해짐. 배당락 시점까지 모두 기억해서 계산을 해야 하는 번거로움 |
이제 주가 모델에 대해서는 많이 익숙해진 듯합니다. 이제부터 주식을 기초자산으로 하는 여러 파생상품들에 대해 다뤄 볼까 합니다. 다음 글에서 이어집니다.
'금융공학' 카테고리의 다른 글
| 파생상품이란? #2 (0) | 2022.07.26 |
|---|---|
| 파생상품이란? #1 (0) | 2022.07.21 |
| GBM의 확장판들 #1. 기대수익률/변동성을 시간함수로! (0) | 2022.07.19 |
| 위험중립측도와 market price of risk (1) | 2022.07.18 |
| GBM 은 어떤 모델일까? (2) | 2022.06.27 |



댓글