이 글은
2022.06.19 - [금융공학] - GBM 주가패스 만들기 #1: 만기시점 주가만
GBM 주가패스 만들기 #1: 만기시점 주가만
이 글은 2022.06.07 - [금융공학] - 주식의 수학적 모델 #3 : GBM모델 주식의 수학적 모델 #3 : GBM모델 이 글은 2022.05.27 - [금융공학] - 주식의 수학적 모델 #1 주식의 수학적 모델 #1 이 글은 2022.05.25 - [..
sine-qua-none.tistory.com
에서 이어집니다. GBM 모델을 사용하여 만기시점 주가만 생성하는 예제를 다뤘습니다. 이제 만기시점뿐만 아니고 만기 때까지 daily로 움직이는 주가 패스를 생성해 내 보도록 하겠습니다.
전의 글에서의 기호들을 그대로 사용합니다.
시점 $t$에서의 주가를 $S_t$라 하고,
- $S_0$ : 현재시점의 주가
- $\mu$ : 주식의 연 수익률
- $\sigma$ : 주식의 연간 수익률의 표준편차, 즉 변동성
이라 할 때, daily 또는 일정 시간 간격으로 주가를 생성하기 위해서는
$$ S_{t_{i+1}} = S_{t_i} \exp\left( \left(\mu-\frac12\sigma^2 \right)(t_{i+1}-t_i) + \sigma (W_{t_{i+1}} -W_{t_i}) \right) \tag{2}$$
형태로 recursively 생성하면 됩니다 (지난 글에서 수식(2)이라고 했으므로 이번 글에서도 수식(2)라 하겠습니다.
1. 수식(2)처럼 특정 시간 간격(ex. Daily)으로 움직이는 주가 패스 만들기
두 가지를 볼 것입니다.
- 첫째는, 만기시점까지 일간으로 움직이는 주가 패스를 만들어 그래프를 그려볼 예정입니다.
둘째로 1번처럼 주가 패스를 만든 뒤, 만기 시점의 주가만 모읍니다. 이것이 그냥 만기 주가만 생성한 경우와 그래프 차이가 있는지, 만기 주가의 평균은 어떻게 되는지 살펴보겠습니다.
python code는 다음과 같습니다.
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import scipy.stats as stats
def make_GBM_path_nSteps():
s0 = 100
mu = 0.02
sigma = 0.2
T = 1
days = 250
dt = 1 / days
nSimulation = 10000
nSteps = T * days
zNormal = np.random.normal(size=(nSteps + 1, nSimulation))
s_process = np.zeros((nSteps, nSimulation))
s_process[0] = s0
drift = (mu - 0.5 * sigma ** 2) * dt
diffusion = sigma * np.sqrt(dt)
for i in range(1, nSteps):
s_process[i] = s_process[i - 1] * np.exp(drift + diffusion * zNormal[i])
s_mat = s_process[-1]
theoretical_avr = s0 * np.exp(mu * T)
print('Average of S_mat is {:.4f}'.format(s_mat.mean()))
print('Theoretical average is {:.4f}'.format(theoretical_avr))
plt.subplot(121)
plt.plot(s_process[:, :30])
plt.title('100 stock paths')
plt.subplot(122)
plt.hist(s_mat, bins=50)
plt.show()
if __name__ == '__main__':
make_GBM_path_nSteps()부분적으로 설명하면 다음과 같습니다.
s0 = 100
mu = 0.02
sigma = 0.2
T = 1
days = 250
dt = T / days현재 시점 주가 $S_0$를 100, 연평균 수익률 $\mu$을 2%, 변동성 $\sigma$를 20%, 만기시점 $T$를 1(year)로 세팅합니다.
저번 글과 다르게 days라는 변수를 정의합니다. 1년 동안의 business day 개수를 말하는 건데요. 토/일요일, 공휴일 등을 제외하면 1년에 주가가 움직이는 영업일은 약 250일이 나옵니다. 따라서 250일로 정의합니다. 이 각각의 날에 해당하는 주가를 생성해 볼 생각입니다. 따라서 주가가 생성되는 시간 간격은
$$ dt = 1/days $$
이겠죠.
nSimulation = 10000
nSteps = T * days
zNormal = np.random.normal(size=(nSteps + 1, nSimulation))
s_process = np.zeros((nSteps, nSimulation))
s_process[0] = s0simulation은 10,000회 정도 해 볼 생각입니다. 그리고 1회당 만들어야 되는 주가는 일간으로 T*days개입니다. 이것을 nSteps 변수에 넣습니다.
그리고! 난수 배열과 주가 배열을 nSteps * nSimulation 정도의 사이즈로 만듭니다. 도식을 보면 아래와 같습니다.

s_process[0] = s0은 각 시뮬레이션에 S 초기값을 모두 S0로 시작한다는 뜻입니다.
drift = (mu - 0.5 * sigma ** 2) * dt
diffusion = sigma * np.sqrt(dt)
for i in range(1, nSteps):
s_process[i] = s_process[i - 1] * np.exp(drift + diffusion * zNormal[i])앞선 글과 마찬가지로, drift와 diffusion을 정의하는데, 여기서 시간 간격을 dt 이죠. 이것을 주의해야 합니다.
그런 다음 수식(2)을 이용하여 재귀적(recursively)으로 주가 패스를 생성합니다.
s_mat = s_process[-1]
theoretical_avr = s0 * np.exp(mu * T)
print('Average of S_mat is {:.4f}'.format(s_mat.mean()))
print('Theoretical average is {:.4f}'.format(theoretical_avr))가장 마지막 행을 얻을 때 보통 index [-1]을 사용합니다. s_process의 마지막 행을 구하려면 s_mat = s_process[-1] 같이 해 주면 됩니다.
앞의 글과 마찬가지로 만기 주가의 평균과, 이론적인 평균을 구합니다.
plt.subplot(121)
plt.plot(s_process[:, :30])
plt.title('30 stock paths')
plt.subplot(122)
plt.hist(s_mat, bins=50)
plt.show()subplot 2개로 이루어진 그래프를 그입니다. 첫 번째 그림에는 s_process[:. :30] 즉, 행(row)으로서는 전체, 열(column)로서는 30번째 열까지, 열은 시뮬레이션 방향을 의미하므로 주가 패스 30개를 그려보자는 얘기입니다.
또 두 번째 그림은 히스토그램인데, s_mat 을 계급구간 50으로 나눠서 그려보자는 겁니다.
자 그럼 결과를 볼까요?
Average of S_mat is 102.1671
Theoretical average is 102.0201
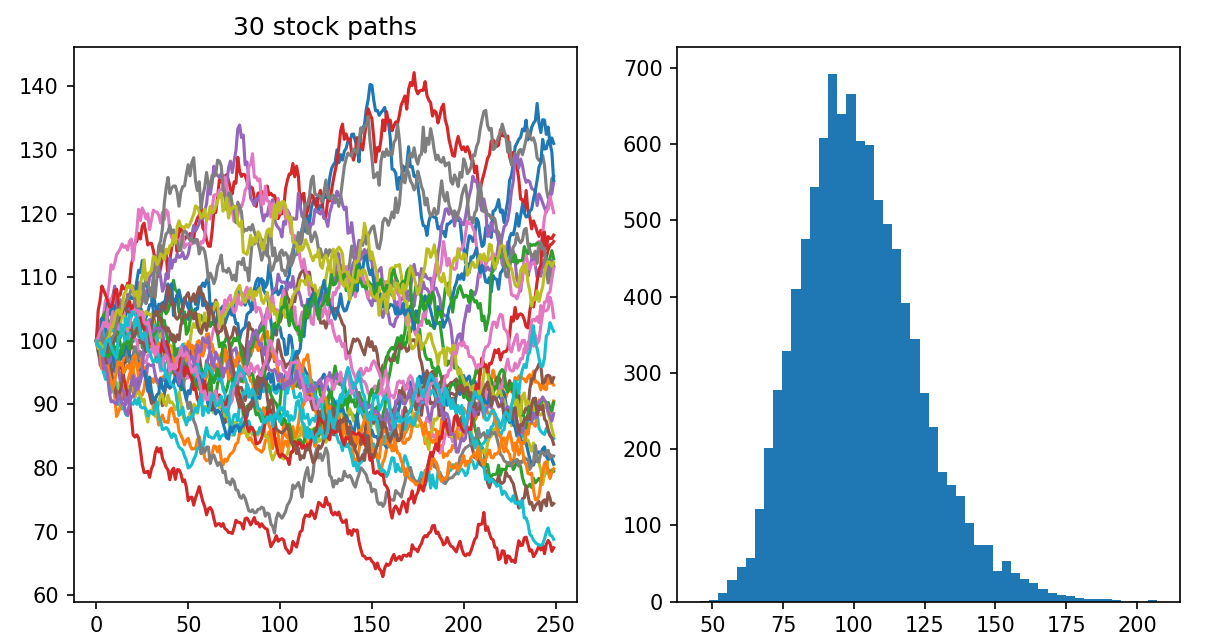
Process finished with exit code 0시뮬레이션하여 얻은 평균과 이론적 평균이 거의 흡사하죠. 그리고 위의 그림의 왼쪽은 가상의 주가 패스 그래프입니다. 그래프 좌측의 시작점은 S0 = 100으로 동일하고, 난수가 어떻게 발생되냐에 따라 주가 패스가 다양하게 결정이 되겠죠.
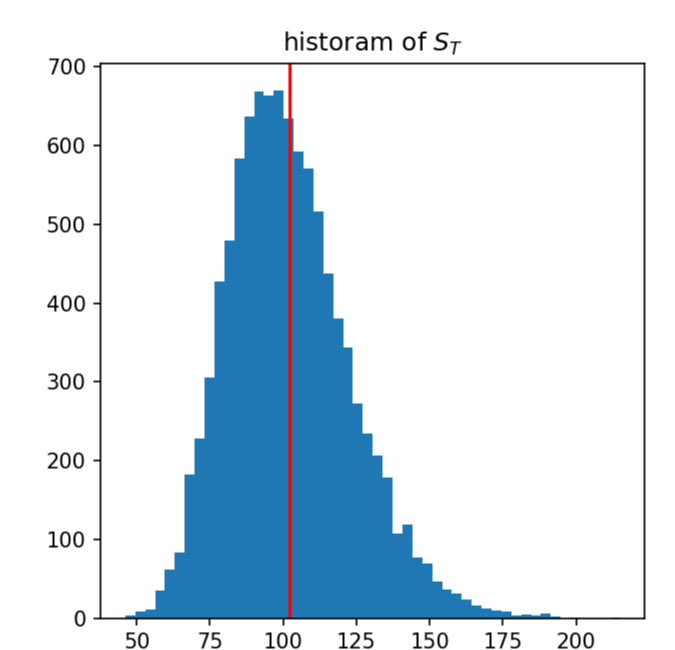
오른쪽은 만기 주가(왼쪽 그래프의 각 주가 패스들이 끝나는 점들)를 모아 히스토그램으로 작성한 겁니다. 이것을 저번 글에서 만기 주가만 뽑아서 그린 아래 그림(저번 글에서 확인 가능)과 비교해 보죠.
분포가 거의 똑같습니다. 즉,
- 하루하루의 주가를 모델링해서 만기까지 step by step으로 가나,
- 만기 주가를 한방에 구하나
차이가 없다는 겁니다. 그럼 왜 하루하루 주가를 모델링하는 것이 필요할까요? 나중에 금융상품을 계산할 때 보시겠지만 하루하루의 주가 예측치가 필요한 상품들이 있기 때문입니다. 예컨대, American option이나 knock in, knock out 처럼 어느 조건을 만족할 때 옵션이 죽거나 살아나는 그런 상품들 평가에 말입니다.
다음 글에서는 GBM 주가 모델의 분포와 기댓값, 분산 등 여러 가지 팩트들을 소개하겠습니다.
'금융공학' 카테고리의 다른 글
| 위험중립측도와 market price of risk (1) | 2022.07.18 |
|---|---|
| GBM 은 어떤 모델일까? (2) | 2022.06.27 |
| GBM 주가패스 만들기 #1: 만기시점 주가만 (0) | 2022.06.19 |
| 주식의 수학적 모델 #3 : GBM모델 (2) | 2022.06.07 |
| 주식의 수학적 모델#2 (0) | 2022.06.01 |




댓글