이번 글은
2022.05.17 - [금융공학] - KOSPI수익률의 표준편차는? #2
KOSPI수익률의 표준편차는? #2
이 글은 2022.05.17 - [금융공학] - KOSPI 수익률의 표준편차는? #1 KOSPI 수익률의 표준편차는? #1 이 글은 KOSPI 지수를 trading 하는 기법에 관련된 것이 아니고, 금융공학적으로 KOSPI의 변동성을 어떻게 측
sine-qua-none.tistory.com
에서 이어집니다. 저번 블로그에서는 KOSPI지수의 NN일 간격 수익률 표준편차의 특징에 대해서 알아봤습니다. 그렇다면 NN일 간격 수익률의 분포는 어떤 모양을 이루고 있을까요?
엑셀 분석을 통해 알아보겠습니다.
1. 수익률 구하기

저번 글에서와 같이 엑셀의 OFFSET 함수를 이용해서 C1셀의 NN을 조절하여 NN일 간격의 수익률을 계산합니다.
이제 C열에 위치한 수익률 2500 개(2012.3.6- 2022.4.29) 의 데이터를 이용해서 히스토그램을 그려보도록 하겠습니다. 엑셀의 분석도구 중 히스토그램을 그리는 분석 도구가 있긴 하지만, 엑셀 내장함수를 이용해서 히스토그램을 그려보도록 하지요.
2. 히스토그램의 계급 구간 설정

히스토그램을 그리기 위해서 계급구간을 설정해야 합니다. 위 그림과 같이 수익률의 최솟값과 최대값을 구해보니 각각 -8.39%, 8.60% 입니다. 따라서 우리는 계급구간을
-9% ~ 9% 사이로 잡으면 1일 수익률을 모두 포함시킬수 있을 것 같습니다. 좀 잘게 0.2% 씩 나누어 계급구간을 구하면
[−9%,−8.8%,−8.6%,⋯,8.6%,8.8%,9%][−9%,−8.8%,−8.6%,⋯,8.6%,8.8%,9%]
입니다.
3. 히스토그램의 계급 구간 별 값 구하기

I열에 계급구간을 써넣고, 구간 개수를 구한다. 예를 들어 계급이 -8.6%인 칸에는
−8.8%<수익률≤−8.6%
인 수익률의 개수를 구하면 됩니다. 한번에 구하기 어려우므로 아래와 같이 보조 열인 누적 개수열(L열)을 만들어 누적 개수를 구해보죠. (아래 그림의 정규분포pdf값은 나중에 써먹을 것이므로 지금은 살짝 무시하죠)

누적개수 구하는 식이
=COUNTIF(C5:C$2504, "<="&I5)
인데,
- C5:C$2504 는 range로써 카운팅하고자하는 범위를 뜻하고,
- "<="$I5는 criteria로써 I5셀에 있는 -9.00% 보다 작거나 같은 데이터의 수를 카운팅 하라는 조건입니다.
이 수식을 9% 까지 drag하여 채우면 당연히 마지막 값은 2500이 나오게 됩니다. 그럼 이를 이용하여 데이터 구간 개수를 어떻게 구할까요?

위의 식처럼 누적개수의 차이를 계산하면 됩니다. 이제 준비가 되었습니다. 차트를 그려봅시다.
4. 히스토그램 차트 그려보기
차트는 세로막대형 차트를 준비합니다.

어떻습니까?
평균으로 보이는 중심에 수익률이 가장 많이 몰려있고
평균(중심)에서 멀어질수록 그 개수는 줄어들고, 양 끝단에는 데이터가 거의 보이지 않습니다.
또한, 중심 좌/우가 대칭형태죠?
바로 아래의 가장 유명한 분포인 벨 모양의 커브, 정규분포 그래프가 떠오릅니다. (위 그림 K열을 준비한 이유!)

5. 히스토그램 차트에 정규분포 그래프 얹어 비교해 보기
마지막으로, 그린 히스토그램에 정규분포 그래프를 얹어 과연 모양이 유사한지 한번 보겠습니다.
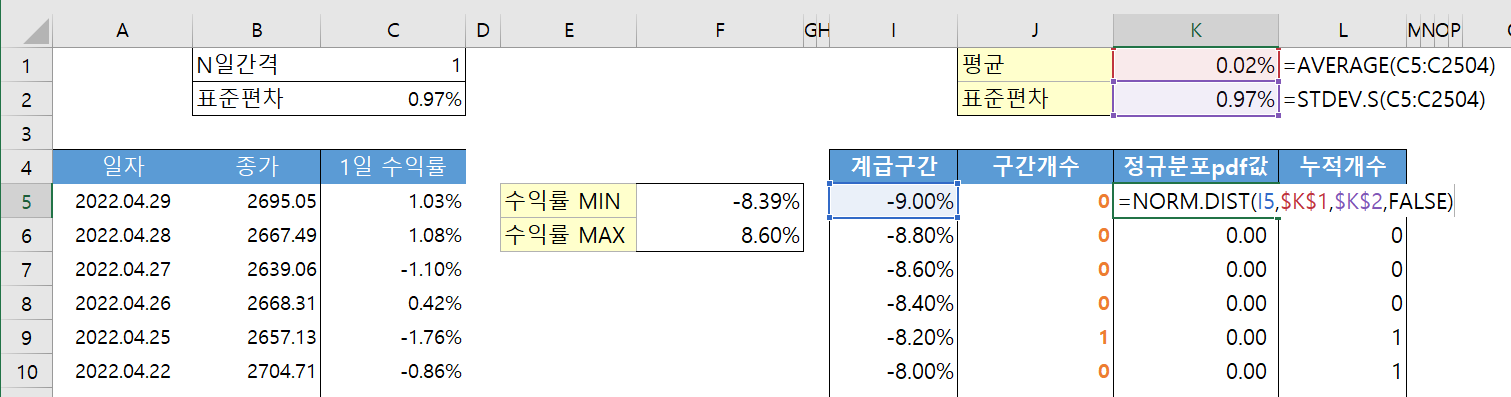
정규분포 그래프를 그리려면 평균과 표준편차가 필요합니다. 위 그림처럼 K1, K2 셀에 각각 AVERAGE와 STDEV.P를 이용하여 평균과 표준편차를 구한 뒤
=NORM.DIST(x, mean, standard_dev, cumulative)
함수를 이용하여 x에서의 정규분포 값을 구합니다. (cumulative 인자를 FALSE로 놓으면 확률밀도함수의 값)
자, 꺽은선 그래프를 얹어 볼까요?
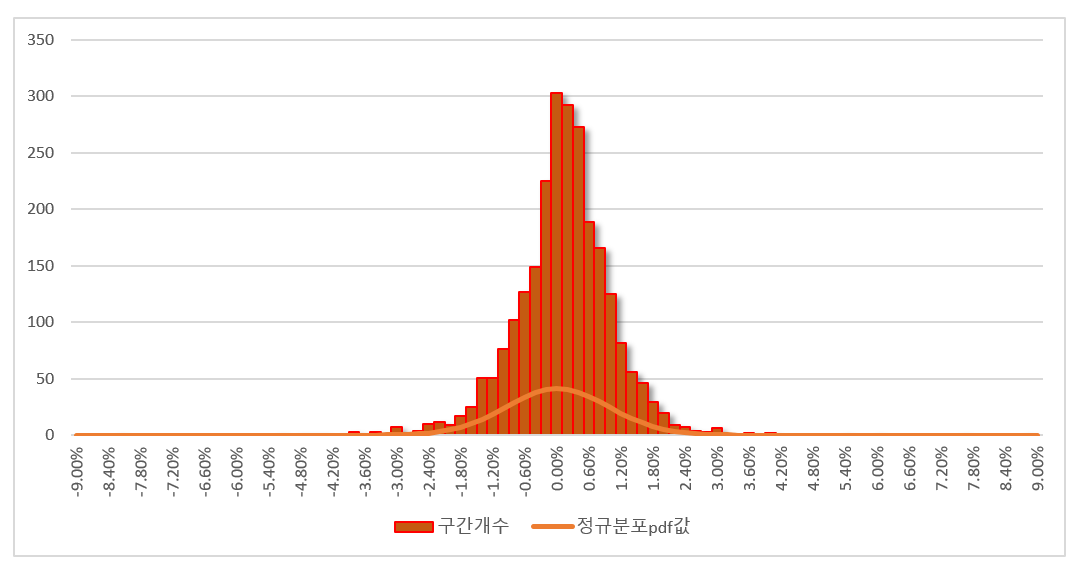
뭔가 이상한데요.. 아, 무작정 얹었더니 스케일을 고려 안했습니다. 히스토그램은 개수이고 꺽은선 정규분포는 함수값이죠. 스케일을 맞춰봅니다. 스케일을 맞춰보는 가장 간단한 방법은 다음과 같아요.
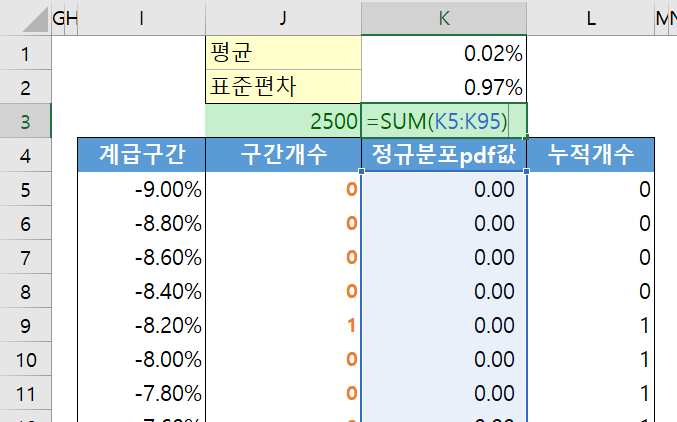
이런식으로 구간개수와 정규분포pdf값 열의 모든 수를 더해보는 겁니다. 그럼 구간개수는 2500, 정규분포pdf값은 500이 나오는데요. 5배수 차이가 나네요. 이제 정규분포pdf값에 5배를 각각 다 해주고 그려보면(아니면 구간개수를 각각 5로 나눠도 됩니다.)
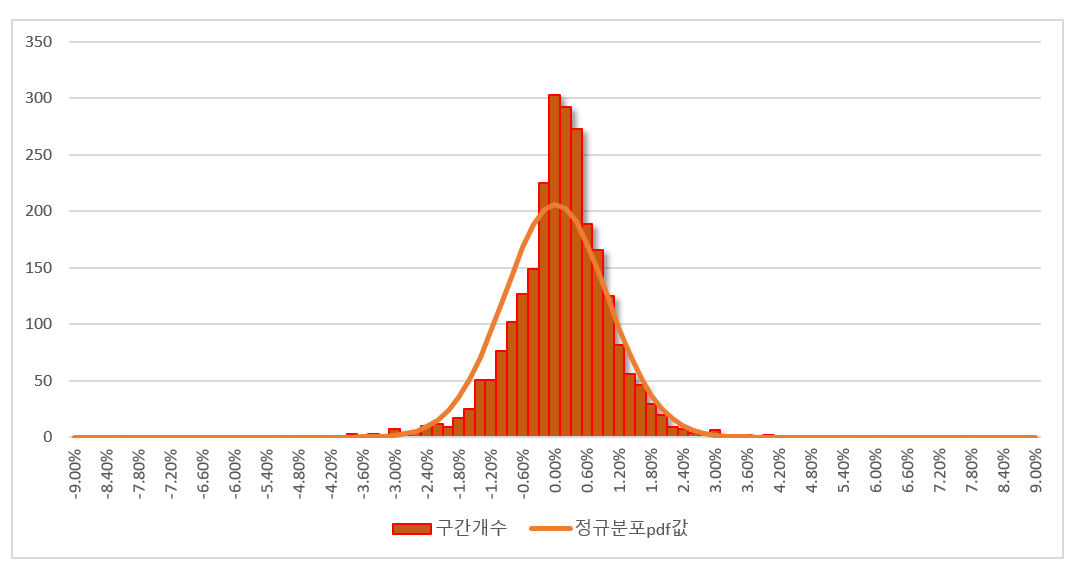
게 됩니다.
어떤가요? 조금 불만족스럽지만 어느 정도 설명이 되는 느낌이 있나요?
우선 퍼져나가는 폭은 상당히 유사합니다. 또한 대칭을 이루는 것도 비슷합니다. 약간 높낮이 차이는 있지만, 이는 스케일링의 문제이기도 하고,
컴퓨터로 정규분포 난수 발생을 시켜 히스토그램을 그려도 딱 맞아 떨어지지 않는다는 사실
을 안다면, 우리는 KOSPI 의 1일수익률의 분포가 정규분포를 형태라고 모델링 해도 꽤 합리적일 것 같습니다.
(사실, 이보다 더 설명력 없는 여러 사회/자연현상들도 정규분포에 때려넣고 분석하는 실정이니까요)
다음 글에서는 1일수익률이 아닌 다른 N일 간격 수익률의 히스토그램도 구경해 볼 수 있도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 주식의 수학적 모델 #1 (4) | 2022.05.27 |
|---|---|
| KOSPI수익률의 분포는 어떤 모양일까? #2 (0) | 2022.05.25 |
| KOSPI 수익률의 표준편차는? #4(로그수익률) (0) | 2022.05.20 |
| KOSPI 수익률의 표준편차는? #3 (로그수익률) (2) | 2022.05.20 |
| KOSPI수익률의 표준편차는? #2 (1) | 2022.05.17 |



댓글