이 글은 로(rho)에 관련된 글 로(Rho)! 콜옵션의 이자율 민감도는?
로(Rho)! 콜옵션의 이자율 민감도는?
이 글은 Vega에 관련된 글 Vega! 변동성에 대한 콜옵션 가격 민감도 Vega! 변동성에 대한 콜옵션 가격 민감도 이 글은 2023.05.26 - [금융공학] - 콜옵션의 움직임을 낱낱이 파헤쳐보자: 민감도 팩터 분석
sine-qua-none.tistory.com
에서 이어집니다. 저번 글에서 콜옵션의 로는 아래와 같다고 했습니다.
콜옵션의 로(rho)
콜옵션 가격이 이자율 $r$의 변화에 얼마나 민감한지를 보는 척도라 그랬죠. 로(rho)는 아래와 같이 정의하고 직접 Black Scholes Formula를 $r$로 미분하여 로를 얻을 수 있습니다.
| 구분 | 정의 | 수식 |
| 로($\rho$,1차 도함수) | $$\rho= \frac{\partial c}{\partial r}$$ | $$ \tau Ke^{-r\tau} \Phi(d_2) \tag{1}$$ |
위의 로 수식 (수식(1))을 보면 $\tau, K, e^{-r\tau}, \Phi(d_2)$ 모두 양수이죠? 따라서 콜옵션의 로는 양수임을 알 수 있습니다. 따라서
$$ \frac{\partial c}{\partial r} >0 $$
이고 이것은 콜옵션의 가격 $c$가 $r$에 대한 증가함수라는 얘기입니다. 이를 간단하게 python code로
Python Code : 콜옵션과 이자율의 관계
먼저 콜옵션 가격 및 민감도 구하는 함수는 아래와 같이 확장됩니다(로를 추가했습니다.)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import pandas as pd
def CallOptionBS(S, K, T, r, q, sigma):
Ncdf = norm.cdf
npdf = norm.pdf
if T == 0:
val = np.maximum(S - K, 0)
delta = 1 if S >= K else 0
gamma = 0
speed = 0
theta = 0
vega = 0
volga = 0
ultima = 0
rho = 0 # rho 추가
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
val = S * np.exp(-q * T) * Ncdf(d1) - K * np.exp(-r * T) * Ncdf(d2)
delta = np.exp(-q * T) * Ncdf(d1)
gamma = np.exp(-q * T) * npdf(d1) / (S * sigma * np.sqrt(T))
speed = -np.exp(-q * T) * npdf(d1) / (S ** 2 * sigma * np.sqrt(T)) * (1 + d1 / (sigma * np.sqrt(T)))
theta = -np.exp(-q * T) * S * npdf(d1) * sigma / (2 * np.sqrt(T)) - r * K * np.exp(-r * T) * Ncdf(
d2) + q * S * np.exp(-q * T) * Ncdf(d1)
vega = S * np.exp(-q * T) * npdf(d1) * np.sqrt(T)
volga = vega * d1 * d2 / sigma
ultima = -vega / sigma ** 2 * (d1 * d2 * (1 - d1 * d2) + d1 ** 2 + d2 ** 2)
rho = T * K * np.exp(-r * T) * Ncdf(d2)
# 0. value
# 1. delta
# 2. gamma
# 3. speed
# 4. theta
# 5. vega
# 6. volga
# 7. ultima
# 8. rho
return val, delta, gamma, speed, theta, vega, volga, ultima, rho # rho 추가 return
이제 위 함수를 가지고 콜옵션 가격과 이자율의 관계를 알아보죠.
def relation_between_call_and_rfr():
s0 = 100
strike = 100
rfr = 0.02
div = 0.01
maturity = 1
vol = 0.3
s_vec = np.arange(10, 150, 1) # 기초자산 grid = 10 ~ 150 까지 1간격
rfr_list = np.arange(-0.05, 0.05 + 0.02, 0.02) # 이자율 list : -5% ~ 5% 까지 2% 간격
from matplotlib import gridspec
fig = plt.figure(figsize=(20, 10))
gs = gridspec.GridSpec(nrows=1, ncols=2, width_ratios=[1, 1])
ax = [fig.add_subplot(gs[0]), fig.add_subplot(gs[1])]
for r in rfr_list: # 이자율을 바꿔가며 for문
res = [CallOptionBS(spot, strike, maturity, r, div, vol)[0] for spot in s_vec]
# 기초자산 grid에 대한 콜옵션 가격 산출
ax[0].plot(s_vec, res, label='rfr={:.2f}%'.format(r * 100))
# 해당 이자율에 대한 콜옵션 가격 그래프
ax[0].legend()
rfr_grid = np.linspace(-0.5, 0.5, 100 + 1) # 이자율 grid를 -50% ~ 50% 까지 100등분
# (이자율이 -50%, 50% 등은 말도 안되지만, '이론적' 분석을 위해 극단적인 상황 도입)
res = [CallOptionBS(s0, strike, maturity, r, div, vol)[0] for r in rfr_grid]
# 고정된 기초자산 가격 s0=100에 대해 이자율 vs 콜옵션 가격 그래프 산출
ax[1].plot(rfr_grid, res, label='rfr vs call_Value') # 이자율 grid에 대한 콜옵션 가격
ax[1].legend()
plt.show()
if __name__ == '__main__':
relation_between_call_and_rfr()
결과는 다음과 같습니다.
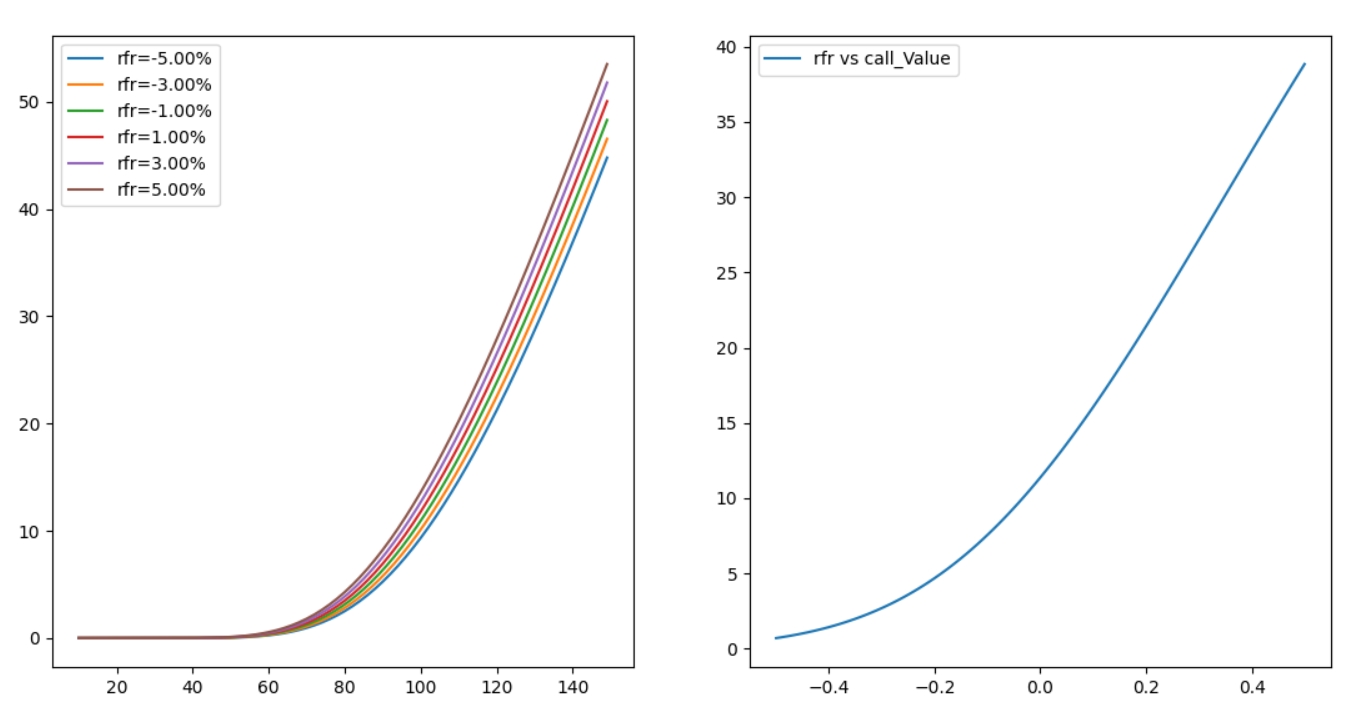
○ 왼쪽 그래프: 이자율이 높아질수록 콜옵션 가격 그래프가 상승한다는 것을 알 수 있습니다. 즉 로(rho)가 양수라는 이야기입니다.
○ 오른쪽 그래프: 고정된 현재가에 대해, 이자율($x$축)과 콜옵션 가격($y$)축 간의 관계를 살펴보는 그래프입니다. 이자율이 증가할수록 콜옵션 가격도 커짐을 알 수 있는데, 커지는 정도가 아래로 볼록인 그래프를 보입니다(이걸 보이느라 이자율을 -50% ~ 50% 로 말도 안 되게 잡아본 것입니다.)
이자율의 변화가 콜옵션 가격 변화에 미치는 영향 요인
예전 글 변동성 변화에 따른 콜옵션 가격 변화 팩터 분석하기
변동성 변화에 따른 콜옵션 가격 변화 팩터 분석하기
이 글에서는, 바로 전 글( 변동성이 커지면 콜옵션 값어치가 올라간다!?) 변동성이 커지면 콜옵션 값어치가 올라간다!? 이 글은 2023.05.31 - [금융공학] - Vega! 변동성에 대한 콜옵션 가격 민감도 Vega!
sine-qua-none.tistory.com
에서는 변동성 변화에 따른 콜옵션 가격 변화를 알아봤었고, 콜옵션의 움직임을 낱낱이 파헤쳐보자: 민감도 팩터 분석
콜옵션의 움직임을 낱낱이 파헤쳐보자: 민감도 팩터 분석
이번 글은 콜옵션 가격 변동 헤지(hedge) 시뮬레이션 콜옵션 가격 변동 헤지(hedge) 시뮬레이션 이번 글은 콜옵션 가격 변동 리스크를 없애보자! 콜옵션 가격 변동 리스크를 없애보자! 이번 글은 콜
sine-qua-none.tistory.com
라는 글에서는 기초자산 변화에 따른 요인분석을 델타, 감마, 스피드로 세분화하여 영향도를 측정해 봤습니다. 그럼 이자율은 어찌 될까요? 아래의 코드를 보시죠.
def analysis_call_option_rfr_risk_factor():
s0 = 100
strike = 100
maturity = 1
rfr = 0.03
div = 0
vol = 0.3
# rfr_after : 변화한 무위험이자율
# drfr : rfr_after - rfr : 즉 이자율 변화
# dc : 콜옵션 가격 변화
# rho_fac : 로에 의한 변화 (rho* drfr)
# 위 4 features로 이루어진 dataframe을 작성한다.
columns = ['rfr_after', 'drfr', 'dc', 'rho_fac']
call0 = CallOptionBS(s0, strike, maturity, rfr, div, vol)
val0, rho0 = call0[0], call0[8] # 무위험이자율이 rfr(=0.03)일 때, 콜옵션 가격과 로(rho)
num_data = 500 # 500개의 sample 추출 예정
rfr_range = 0.2 # 무위험이자율이 변화는 범위를 위아래로 0.2까지
df = pd.DataFrame(data=[], columns=columns)
rfr_change = np.random.uniform(rfr - rfr_range, rfr + rfr_range, num_data)
# rfr에서 위아래로 rfr_range까지 범위에서 균등난수 발생
call_vec = np.array([CallOptionBS(s0, strike, maturity, r, div, vol)[0] for r in rfr_change])
# 위 난수 이자율에 대응하는 call option value 추출
df['rfr_after'] = rfr_change
df['drfr'] = rfr_change - rfr
df['dc'] = call_vec - val0
df['rho_fac'] = rho0 * df['drfr']
df['1fac_effect'] = df.dc - df.rho_fac # 콜옵션 가격의 변화를 이자율 변화가 얼만큼 따라가는지
pd.set_option('display.max_columns', None)
print(df)
df_mean = df[['1fac_effect']].mean()
print(df_mean)
plt.scatter(df['drfr'], df['1fac_effect'], label='rfr change vs effectness error')
# 이자율 변화 vs 로 팩터의 경향성 그림
plt.legend()
plt.show()
위 코드의 내용은 이렇습니다. 콜옵션 가격 $c(t,S)$의 한 파라미터인 무위험 이자율이 $r$에서 $r+\Delta r$로 바뀔 때, 테일러 전개에 따르면
$$ c(t,S;r+\Delta r) - c(t,S;r) \approx \frac{\partial c}{\partial r} (t,S) \cdot (\Delta r)$$
입니다. 따라서 위 코드의 변수로 설명하면
df['dc'] ~ df['rho_fac']라는 이야기죠. 물론 근사치라
df['1fac_effect'] = df.dc - df.rho_fac위의 값이 살아 있을 것입니다. 이 차이값은 이자율에 대한 2차 편미분, 고차 편미분 등으로 설명될 수 있을 것입니다. 중요한 것은, 이자율의 변화가 클수록, 즉, drfr이 증가할수록 근사값 에러인 1fac_effect가 커지리라는 사실입니다. 결과를 한번 보시죠.
C:\Users\kimju\PycharmProjects\StockProject\venv\Scripts\python.exe C:/Users/kimju/PycharmProjects/StockProject/TaylorApproximation.py
rfr_after drfr dc rho_fac 1fac_effect
0 0.009126 -0.020874 -0.954267 -0.972477 0.018209
1 0.198390 0.168390 8.828336 7.844846 0.983489
2 0.080365 0.050365 2.446439 2.346388 0.100051
3 0.113898 0.083898 4.177390 3.908605 0.268786
4 0.220281 0.190281 10.085482 8.864680 1.220802
.. ... ... ... ... ...
495 0.176185 0.146185 7.572068 6.810360 0.761708
496 0.027737 -0.002263 -0.105214 -0.105425 0.000211
497 0.068905 0.038905 1.872812 1.812493 0.060319
498 -0.141696 -0.171696 -6.671770 -7.998861 1.327092
499 0.034473 0.004473 0.209211 0.208390 0.000821
[500 rows x 5 columns]
1fac_effect 0.510831
dtype: float64
콜옵션의 변화가 로(rho)로 설명되지 않는 부분 즉, 1fac_effect 의 평균은 0.5로 제법 큽니다. 이 차이는 당연히 이자율에 대한 2차, 3차 편미분 등으로 채워질 수 있을 것입니다. 하지만 그걸 따져보지 않는 이유는 어째서인지 금융공학에서 이자율에 대한 고차 편미분 그릭은 별로 다루지를 않습니다. 기초자산에 대한 2차 미분인 감마, 변동성의 2차 미분인 볼가에 대해서는 자세히 다루는 데 말이죠.
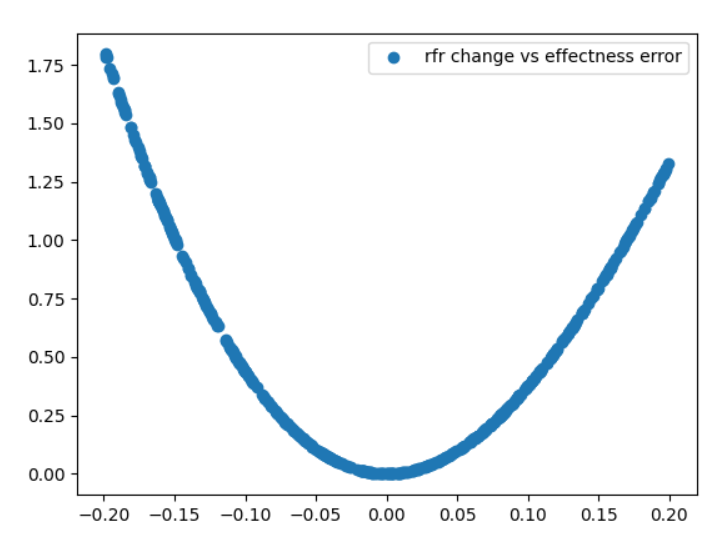
$x$축을 이자율의 변화, $y$축을 1차 근사 에러로 하는 그래프를 그리면 아래와 같습니다. 2차 곡선 형태가 나오지요. 이유는,
$$ c(t,S;r+\Delta r) - c(t,S; r) \approx \frac{\partial c}{\partial r} (\Delta r) +\frac12 \frac{\partial^2 c}{\partial r^2} (\Delta r)^2 $$
에서 우변의 2번째 항
$$ \frac{\partial^2 c}{\partial r^2} (\Delta r)^2$$
이 오차항으로 작용하고, 이것이 $\Delta r$의 제곱항으로 표현돼서 그런 것입니다.
정리
지금까지 몇개의 글에 걸쳐 콜옵션의 민감도를 알아봤습니다.
기초자산 민감도 델타, 감마, 스피드, 시간변화에 따른 민감도, 변동성 관련 민감도인 베가, 볼가, 마지막으로 이자율에 따른 민감도인 로(rho) 까지!
보통 파생상품의 가격 변동을 설명하는 민감도는 위에 언급한 것들로 거의 다 설명이 됩니다만, 기초자산의 변동폭이 크거나, 변동성, 이자율 등 파라미터가 급변하는 시장상황에서는 또 설명 안 되는 부분들이 있습니다. 이 설명안되는 부분들은 고차 편미분 민감도나 아니면 교차 편미분(cross term)으로 설명을 해야 합니다만, 글이 너무 지엽적으로 흐를 수 있으니 민감도에 대한 설명은 이쯤 하도록 하겠습니다.
지금까지 콜옵션의 민감도에 대해서 알아봤는데요, 다음글에서는 풋옵션의 민감도는 어찌 될지 한번 알아보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 그릭을 수치 해석적인 방법으로 해결하기 (0) | 2023.06.23 |
|---|---|
| 풋옵션의 민감도들은? feat. 풋콜패리티 (0) | 2023.06.19 |
| 로(Rho)! 콜옵션의 이자율 민감도는? (0) | 2023.06.09 |
| 변동성 변화에 따른 콜옵션 가격 변화 팩터 분석하기 (0) | 2023.06.05 |
| 변동성이 커지면 콜옵션 값어치가 올라간다!? (0) | 2023.06.01 |

댓글