이 글은
2023.05.31 - [금융공학] - Vega! 변동성에 대한 콜옵션 가격 민감도
Vega! 변동성에 대한 콜옵션 가격 민감도
이 글은 2023.05.26 - [금융공학] - 콜옵션의 움직임을 낱낱이 파헤쳐보자: 민감도 팩터 분석 콜옵션의 움직임을 낱낱이 파헤쳐보자: 민감도 팩터 분석 이번 글은 콜옵션 가격 변동 헤지(hedge) 시뮬레
sine-qua-none.tistory.com
에서 이어집니다. 위 글에서는 파생상품의 변동성에 대한 민감도를 알아봤습니다. 콜옵션 가격의 변동성 민감도를 복습해볼까요?
콜옵션의 변동성에 관한 민감도
콜옵션의 가격을 $c(t, S)$라 쓰더라도, 콜옵션의 가격을 산정할 때는 변동성, 무위험 이자율, 배당률 등이 변수로 투입되고, 이 중에 특히 변동성에 대한 민감도에는 Vega, Volga, Ultima가 있다고 했습니다. 수식으로 써보면 다음과 같습니다.
| 구분 | 정의 | 수식 |
| 1차 도함수 (Vega) |
$$\mathcal{V}= \frac{\partial c}{\partial \sigma}$$ | $$Ke^{-r\tau} \phi(d_2) \sqrt{\tau}= Se^{-r\tau}\phi(d_1) \sqrt{\tau}$$ |
| 2차 도함수 (Volga) |
$$\frac{\partial^2 c}{\partial \sigma^2}$$ | $$ {\rm{(Vega)}} \frac{d_1d_2}{\sigma} $$ |
| 3차도함수 (Ultima) |
$$\frac{\partial^3 c}{\partial \sigma^3}$$ | $$ -\frac{1}{\sigma} {\rm{Vega}}\cdot \left( d_1d_2(1-d_1d_2) + d_1^2+d_2^2 \right)$$ |
변동성과 콜옵션 가격 간의 관계는?
기초자산의 변동성이 커진다는 것은 기초자산 움직임이 활발해진다는 이야기입니다. 상승이던 하락이던, 그 움직임의 폭이 커진다는 이야기죠.
콜옵션의 페이오프 구조는, 기초자산($S$)이 행사가($K$) 보다 커지면 행사를 하여 $S-K$ 만큼의 수익이 발생하고, 행사가보다 작은 영역에서는 행사 권리가 포기되어 아무런 손익이 발생하지 않습니다. 따라서
기초자산이 아무리 움직여도 하방은 0으로 막혀 있는 구조, 반면 상방은 뚫려 있다!!
가 되는 것이죠. 하락폭이 행사가에 의해 막혀 버렸으니 오히려 좋습니다. 상승폭이 클 때 옵션의 가치는 더더욱 올라가는 것이죠.
따라서 직관적으로
기초자산 움직임이 활발하면 더 많은 콜옵션 수익을 기대할 수 있다.
즉,
콜옵션 가치가 증가한다!
라는 결론이 나옵니다. 즉 콜옵션 가치는 변동성에 대해 증가함수입니다.

위의 예제 그림 중 일부를 그린 python code
x = np.linspace(0, 10, 1001)
y = np.exp(0.3 * x) * np.sin(2 * np.pi * x) + 100
app_y = np.exp(0.3*x)+100
k = 100 * np.ones(len(x))
from matplotlib import gridspec
fig = plt.figure(figsize=(20, 20))
gs = gridspec.GridSpec(nrows=1, ncols=2, width_ratios=[1, 1])
ax = [fig.add_subplot(gs[0]), fig.add_subplot(gs[1])]
ax[0].plot(x, y, label='stock path')
ax[0].plot(x, k, label='strike')
ax[0].legend()
itm_condition = y > k
otm_condition = ~itm_condition
ax[1].plot(x[itm_condition], y[itm_condition], color='red', label='itm region')
ax[1].plot(x[otm_condition], y[otm_condition], color='lightgray', label='otm region')
ax[1].plot(x, app_y, color='blue', linestyle='dashed')
plt.show()
위 그림은 보면, 왼쪽 그름에서 주가 흐름이 오른쪽으로 갈수록 커지는 상황일 때, 콜옵션 페이오프가 결정되는 원리는 오른쪽 그림처럼 되며, 따라서 하방은 막혀 있고 한없이 커지는 상방이 콜옵션 가치를 끌어올린다는 사실을 볼 수 있습니다.
이는 수식으로도 증명할 수 있습니다. 베가의 식은 아래와 같습니다.
$$\mathcal {V} = Ke^{-r\tau} \phi(d_2) \sqrt {\tau}= Se^{-r\tau}\phi(d_1) \sqrt {\tau}$$
그런데, $K$, $e^{-r\tau}$, $\phi(d_2)$, $\sqrt {\tau}$ 모두 양수이죠. 따라서 Vega는 양수입니다. 즉, 콜옵션 가격 $c$를 $\sigma$로 (편) 미분한 값이 양수이므로 $\sigma$에 대한 증가함수가 됩니다.
콜옵션 가격 vs 변동성
변동성이 커질수록 콜옵션 가격이 증가함을 python coding을 통해 알아보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import pandas as pd
# ----------------------------------------
# call option value/Greeks function
# vega, volga, ultima 추가 (theta2 삭제)
# ----------------------------------------
def CallOptionBS(S, K, T, r, q, sigma):
Ncdf = norm.cdf
npdf = norm.pdf
if T == 0:
val = np.maximum(S - K, 0)
delta = 1 if S >= K else 0
gamma = 0
speed = 0
theta = 0
vega = 0
volga = 0
ultima = 0
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
val = S * np.exp(-q * T) * Ncdf(d1) - K * np.exp(-r * T) * Ncdf(d2)
delta = np.exp(-q * T) * Ncdf(d1)
gamma = np.exp(-q * T) * npdf(d1) / (S * sigma * np.sqrt(T))
speed = -np.exp(-q * T) * npdf(d1) / (S ** 2 * sigma * np.sqrt(T)) * (1 + d1 / (sigma * np.sqrt(T)))
theta = -np.exp(-q * T) * S * npdf(d1) * sigma / (2 * np.sqrt(T)) - r * K * np.exp(-r * T) * Ncdf(
d2) + q * S * np.exp(-q * T) * Ncdf(d1)
# theta2 = -(r - q) * S * delta - 0.5 * sigma ** 2 * S ** 2 * gamma + r * val
# theta +(r-q)S *delta + 0.5*sigma^2*S^2 *gamma -rf =0
vega = S * np.exp(-q * T) * npdf(d1) * np.sqrt(T) # vega
volga = vega * d1 * d2 / sigma # volga
ultima = -vega / sigma ** 2 * (d1 * d2 * (1 - d1 * d2) + d1 ** 2 + d2 ** 2) #ultima
# return index
# 0. value
# 1. delta
# 2. gamma
# 3. speed
# 4. theta
# 5. vega
# 6. volga
# 7. ultima
return val, delta, gamma, speed, theta, vega, volga, ultima
def relation_between_call_and_volatility():
strike = 100
rfr = 0.02
div = 0.01
maturity = 1
s_vec = np.arange(10, 150, 1)
vol_vec = np.arange(0.1, 1 + 0.1, 0.1) # volatility를 10%, 20%, ~ , 100% 로 설정
from matplotlib import gridspec # gridspec을 사용하여 plot 구성
fig = plt.figure(figsize=(20, 20))
gs = gridspec.GridSpec(nrows=1, ncols=2, width_ratios=[1, 1])
ax = [fig.add_subplot(gs[0]), fig.add_subplot(gs[1])]
for i in range(len(vol_vec)):
call_value = [] # 각 volatility 에 대해 call value 담을 list 설정
call_gamma = [] # 각 volatility 에 대해 call gamma 담을 list 설정
for s in s_vec:
res = CallOptionBS(s, strike, maturity, rfr, div, vol_vec[i]) # call information
call_value.append(res[0]) # index 0 : call value
call_gamma.append(res[2]) # index 2 : call gamma
call_value = np.array(call_value) # list를 array로 변환
call_gamma = np.array(call_gamma)
# ax[0](왼쪽 ax)에 변동성에 따른 call value를
# ax[1](오른쪽 ax)에 변동성에 따른 gamma graph를 그림
ax[0].plot(s_vec, call_value, label='volatility: {:.2f}%'.format(vol_vec[i] * 100))
ax[1].plot(s_vec, call_gamma, label='volatility: {:.2f}%'.format(vol_vec[i] * 100))
# ax[0]에 내재가치(instrinsic value)도 그려봄
ax[0].plot(s_vec, np.maximum(s_vec - strike, 0), color='black', label='intrinsic value', linestyle='-')
ax[0].set_title('relation between call price and volatility')
ax[1].set_title('relation between call gamma and volatility')
ax[0].legend()
ax[1].legend()
plt.show()
if __name__ == '__main__':
relation_between_call_and_volatility()
자세한 사항은 code의 주석을 참고하시기 바랍니다. 결과를 보겠습니다.
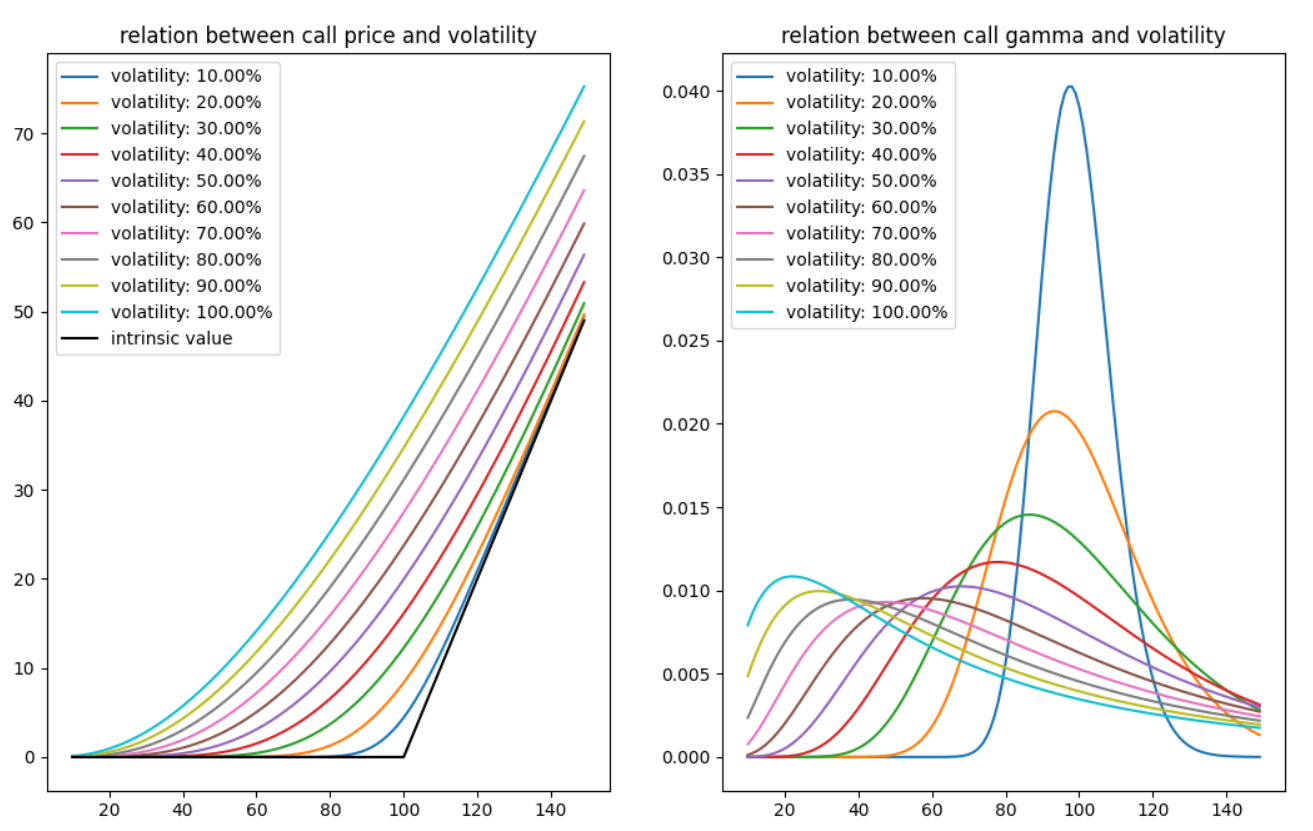
왼쪽 그림 : 변동성에 따른 콜옵션 가격
내재가치선이 검은색 선(제일 아래 위치)이고 변동성이 커질수록 콜옵션 가격 그래프가 붕 떠오르게 됩니다. 이건 콜옵션의 베가가 양수, 즉, 변동성이 커지면 콜 가격이 커지는 현상 때문임을 알 수 있습니다.
또 하나 관찰 가능한 것이 변동성이 커질수록 곡선의 휘는 정도(곡률)가 밋밋해집니다. 제일 변동성이 클 때를 보시죠. 변동성이 100% 일 땐데, 밋밋하게 휘어져 올라가는 것을 보일 수 있습니다.
따라서 감마를 생각해 봤습니다. 감마는 콜옵션 가격을 기초자산 가격으로 두 번 미분한 것으로, 그래프의 곡률(cuvatture)과 관련 있습니다. 그래서.. 감마를 그려 봤습니다.
오른 쪽 그림 : 변동성에 따른 콜옵션 감마
감마가 제일 높이 올라가는 파란색 선은, 변동성이 제일 작은 10% 때 나타나고, 감마 그래프의 고점은 변동성이 커지면서 차츰 낮아지게 됩니다.
이제 콜옵션과 변동성의 관계를 간략히 살펴봤으니 다음 글에서는 변동성의 변화에 따른 콜옵션 변화가 Vega, Volga, Ultima로 어떻게 설명될 수 있는지 한번 알아보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 로(Rho)! 콜옵션의 이자율 민감도는? (0) | 2023.06.09 |
|---|---|
| 변동성 변화에 따른 콜옵션 가격 변화 팩터 분석하기 (0) | 2023.06.05 |
| Vega! 변동성에 대한 콜옵션 가격 민감도 (0) | 2023.05.31 |
| 콜옵션의 움직임을 낱낱이 파헤쳐보자: 민감도 팩터 분석 (0) | 2023.05.26 |
| 세타: 기초자산이 죽어있어도 옵션 가격은 변하더라!? (0) | 2023.05.22 |

댓글