콜옵션의 움직임을 낱낱이 파헤쳐보자: 민감도 팩터 분석

 

 

 

 

이번 글은 콜옵션 가격 변동 헤지(hedge) 시뮬레이션

콜옵션 가격 변동 헤지(hedge) 시뮬레이션

를 정교하게 가다듬어 보겠습니다.

 

 

 

위 글에서 기초자산의 변화에 따른 콜옵션의 가격 변동을 헤지(hedge)하기 위해 기초자산을 샀다 팔았다 하고, 그 사고파는 개수는 콜옵션의 델타(delta) 개만큼이라고 했습니다. 하지만, 

 

시점 변화에 따른 콜옵션 가격의 변화는 고려하지 않는다

 

라는 가정을 했었습니다. 자세히 말해서,  콜옵션 매도포지션을 기초자산으로 헤지할 때, 아래 수식의 "계산 시점 변화에 따른 변동분"을 무시하고 오로지 델타 헤지만 해보았던 것이었죠. 바로 아래처럼요

$$
\begin{align}
c(t_{i+1}, S_{i+1} ) - c(t_i, S_i ) & =c(t_{i}, S_{i+1} ) - c(t_i, S_i ) + c(t_{i+1}, S_{i+1} ) - c(t_i, S_{i+1} )\\
& =  c(t_{i}, S_{i+1} ) - c(t_i, S_i ) + \rm{(계산 시점~ 변화에~ 따른~  변동분)}\\
& = \frac{\partial c}{\partial S}(t_i, S_i) (S_{i+1}-S_i) + 0\tag {1}
\end {align}
$$

 

또한 위 글에서 500개의 주가패스에 대해 콜옵션 매도포지션을 델타 헤지 시뮬레이션 해보니,

hedge p&l mean : 1.43   # hedge 손익 평균
hedge p&l std  : 1.0    # hedge 손익 표준편차

와 같은 결론도 얻었습니다.

 

좀 이상한 부분이 있죠. 헤지라는 것은 콜옵션 매도 포지션의 가격 변동 위험(risk)을 기초자산을 샀다 팔았다 하며 네팅하여 제로를 만드는 것인데, 손익이 +1.43 정도로 플러스 방향으로 발생하죠. (이 결과는   콜옵션 가격 변동 헤지 시뮬레이션: 주가가 만기까지 횡보한다면..라는 글에서도 볼 수 있습니다. 이 때는 헤지성과 평균이 +2.27 나왔습니다.)

 

헤지가 잘됐다면 망외의 수익이 발생해서는 안됩니다. +1.43이나, +2.27등이 아닌, 0 근처의 어떤 수가 나와야 하는 거죠.

 

 

어떤 이유인지 자세하게 살펴보도록 하겠습니다.

 

 

좀 더 자세한 테일러 전개

 

사실 식(1)과 같은 테일러 전개는 비약이 많죠. 제대로 테일러 전개를 해보겠습니다.

 

콜옵션 가격 $c(t, S)$는 이변수 함수입니다. 이변수 함수에 대한 테일러 전개는 테일러 전개 #2 - 다변수의 테일러 전개

테일러 전개 #2 - 다변수의 테일러 전개

에서 다룬 바 있습니다.

 

시점 $t$와 기초자산 $S$의 조금씩의 변화를 각각 $\Delta t, \Delta S$라 하면

 

$$
\begin{align}
 c(t+\Delta t, S+\Delta S) -& c(t,S) = \frac{\partial c}{\partial t} (\Delta t) +\frac12\frac{\partial^2 c}{\partial t^2} (\Delta t)^2+\cdots\\
& + \frac{\partial c}{\partial S} (\Delta S) +  \frac12\frac{\partial^2 c}{\partial S^2} (\Delta S)^2+\frac16 \frac{\partial^3 c}{\partial S^3} (\Delta S)^3 +\cdots \\ 
&  + \frac{\partial^2 c}{\partial t\partial S} (\Delta t)(\Delta S) +\cdots\tag{2}
\end{align}
$$

 

가 성립합니다. 즉, $t$에 대한 테일러 전개, $S$에 대한 테일러 전개를 각각 하고, $t, S$가 혼재된 교차항(cross term)까지 고려하여 테일러 전개가 됩니다. 하지만, $\Delta t$는 통상 하루를 뜻하는 $\frac1 {250}$ 정도로 굉장히 작은 수 이기 때문에 $dt$ 의 2차 이상의 제곱 및 $dt\cdot dS$ 형태의 항은 우선 무시하기로 하죠(그래야 식도 간결해집니다.)

 

그러면 식(2)은 아래와 같이 팍 줄일 수 있게 됩니다.

 

$$
\begin{align}
c(t+\Delta t,& S+\Delta S) - c(t,S) \\
&\approx \frac{\partial c}{\partial t} (\Delta t) +\frac{\partial c}{\partial S} (\Delta S) +  \frac12\frac{\partial^2 c}{\partial S^2} (\Delta S)^2+\frac16 \frac{\partial^3 c}{\partial S^3}(\Delta S)^3 \tag{3}
\end{align}
$$

 

식(3)의 둘째 줄에 등장하는 편미분량은 순서대로 세타, 델타, 감마, 스피드입니다(사실, 스피드까지도 필요 없습니다. 값이 굉장히 작거든요.)

 

식 (3)를 다시 써보면,

$
\begin{align}
c(t+\Delta t,& S+\Delta S) - c(t,S) \\
&\approx {\rm{Theta}}\cdot(\Delta t) +{\rm{Delta}}\cdot (\Delta S) +  \frac12{\rm{Gamma}}\cdot (\Delta S)^2+\frac16 {\rm{Speed}}\cdot(\Delta S)^3\tag{4}
\end{align}
$$

 

입니다.  글 콜옵션 가격 변동 헤지(hedge) 시뮬레이션에서 시점 $t$의 변화는 무시하고  감마, 스피드는 아예 생각하지도 않았던 식

 

$$
\begin{align}
c(t+\Delta t, S+\Delta S) - c(t,S) \approx {\rm{Delta}}\cdot (\Delta S) 
\end{align}
$$

 

와는 천양지차이죠. 이제 식 (4)가 제대로 작동하는 식인지 python coding을 통하여 알아보겠습니다.

 

이른바

민감도 팩터 분석

 

입니다. 민감도 팩터 분석이란, 식(4)에서 보시는 것처럼 

(좌변) 파생상품의 가격 차이를

(우변) 세타에 의한 가격차이, 델타에 의한 가격 차이, 감마에 의한 가격 차이 등으로 원인을 분석해 보는 것을 말합니다.

 

 

 

python code : 콜옵션의 민감도 팩터 분석

 

코드 내용은 이렇습니다.

행사가 100, 만기 $T=1$y 인 콜옵션의 기초자산 현재 가격이 $S_0=100$일 때(즉, ATM인 경우)

 

1) 하루 뒤의 주가 $S_1$ 생성  및 $\Delta S = S_1-S_0$

 

2) 콜옵션 매수 포지션에서 발생한 평가 손익 계산 : 현재 시점을 $t_0=0$, 내일 시점을 $t_1 = \frac1{250}$이라 할 때,

 $$ c(t_1,S_1) - c(t_0,S_0)$$ 계산

 

3) $t_0=0$ 시점에서 구한 세타, 델타, 감마, 세타를 이용하여 근사식 (4)가 맞는지 확인

 

그림으로 표현하면 이렇습니다.

 

 

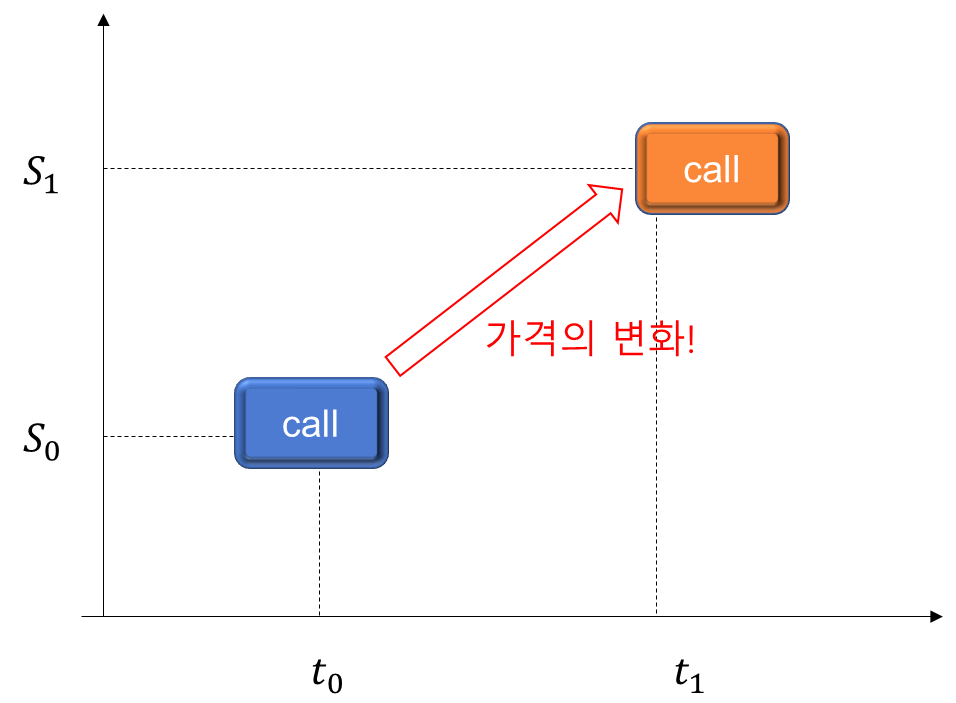
현재시점의 파란 콜이 하루가 지나고($\Delta t = t_1-t_0$) , 주가가 바뀌면서($S_0\rightarrow S_1$) 가격이 주황색 콜로 변할 것입니다. 이 변한 정도를 파란색 콜 시점에 구해진 세타, 델타, 감마, 스피드로 식 (4)처럼 분해해 보자는 이야기죠.

 

 

코드를 보겠습니다.

 

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import pandas as pd


# call option value / sensitivity function
def CallOptionBS(S, K, T, r, q, sigma):
    Ncdf = norm.cdf
    npdf = norm.pdf

    if T == 0:
        val = np.maximum(S - K, 0)
        delta = 1 if S >= K else 0
        gamma = 0
        speed = 0
        theta = 0
        theta2 = 0
    else:
        d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
        d2 = d1 - sigma * np.sqrt(T)
        val = S * np.exp(-q * T) * Ncdf(d1) - K * np.exp(-r * T) * Ncdf(d2)
        delta = np.exp(-q * T) * Ncdf(d1)
        gamma = np.exp(-q * T) * npdf(d1) / (S * sigma * np.sqrt(T))
        speed = -np.exp(-q * T) * npdf(d1) / (S ** 2 * sigma * np.sqrt(T)) * (1 + d1 / (sigma * np.sqrt(T)))
        theta = -np.exp(-q * T) * S * npdf(d1) * sigma / (2 * np.sqrt(T)) - r * K * np.exp(-r * T) * Ncdf(
            d2) + q * S * np.exp(-q * T) * Ncdf(d1)
        theta2 = -(r - q) * S * delta - 0.5 * sigma ** 2 * S ** 2 * gamma + r * val
        # theta +(r-q)S *delta + 0.5*sigma^2*S^2 *gamma -rf =0
    return val, delta, gamma, speed, theta, theta2


def analysis_risk_factor():
    s0 = 100      # current spot =100
    strike = 90   # strike = 90
    maturity = 1  
    rfr = 0.03
    div = 0
    vol = 0.3

    dt = 1 / 250
    sqrtdt = np.sqrt(dt)

    drift = rfr - div - 0.5 * vol ** 2
    columns = ['spot', 'ds', 'dc', 'delta_fac', 'gamma_fac', 'speed_fac', 'theta_fac']
    call0 = CallOptionBS(s0, strike, maturity, rfr, div, vol)  # t=0 에서의 call opt. value/greeks

    data = []
    num_data = 100
    for _ in range(num_data):
        rand = np.random.normal()
        s_after = s0 * np.exp(drift * dt + sqrtdt * rand)  # 하루 뒤 주가 생성
        dspot = s_after - s0                               # 주가 변화량 dS
        # 하루 뒤 주가와 1day 줄어든 잔존만기에 따라 call option value/greek 구하기
        call_after = CallOptionBS(s_after, strike, maturity - dt, rfr, div, vol) 
        
        dcall = call_after[0] - call0[0]  # call option 가격 변화
        delta_factor = call0[1] * dspot   # 델타팩터 = (t=0 시점 delta )* dS
        gamma_factor = 0.5 * call0[2] * dspot ** 2  #감마팩터: (1/2)*(t=0시점 gamma)*(dS)^2
        speed_factor = (1 / 6) * call0[3] * dspot ** 3 # 스피드팩터: (1/6)*(t=0 시점 speed)*(dS)^3
        theta_factor = call0[4] * dt #세타 팩처 : (t=0시점 theta)*dt
        
        # 하루 뒤 주가, dS, dCall, 델타,감마,스피드,세타 팩터를 list로 만듬
        res = [s_after, dspot, dcall, delta_factor, gamma_factor, speed_factor, theta_factor]
        
        # list의 list로 data set 구성
        data.append(res)

    df = pd.DataFrame(data=data, columns=columns)  # pandas dataframe 설계
    
    # 식(4) 구성
    # call option 가격 변화에서 (theta + delta + gamma +speed factor)를 빼면
    # 식(4)의 approximation의 error term이 됨. 이걸 residue column에 저장
    df['residue'] = df.dc - df.theta_fac - df.delta_fac - df.gamma_fac - df.speed_fac
    
    # 그냥 델타 헤지만 했을 때, 즉 call option 변화 - delta factor
    df['delta_hedge_residue'] = df.dc - df.delta_fac
    
    # df 각 column 별로 평균 구함
    df_mean = df.mean(axis=0)

    # df 출력
    # delta hedge만 했을 때의 approximation error 평균 출력
    # delta factor 뿐 아니라, 모든 greeks factor 감안했을 때, error 평균 출력
    pd.set_option('display.max_columns', None)  # df의 모든 column이 보이게 출력

    print(df)
    print('average of delta hedge error is {:.4f}'.format(df.delta_hedge_residue.mean()))
    print('average of approximation error is {:.4f}'.format(df.residue.mean()))
    print(df_mean)

if __name__ == '__main__':
    analysis_risk_factor()

 

결과를 보시죠.

          spot        ds        dc  delta_fac  gamma_fac  speed_fac  \
0   102.329373  2.329373  1.694612   1.691468   0.030113  -0.000702   
1    99.734994 -0.265006 -0.218541  -0.192434   0.000390   0.000001   
2   101.369085  1.369085  0.978049   0.994157   0.010402  -0.000143   
3    92.941176 -7.058824 -4.856072  -5.125745   0.276527   0.019546   
4    92.616392 -7.383608 -5.063034  -5.361586   0.302559   0.022370   
..         ...       ...       ...        ...        ...        ...   
95  101.182007  1.182007  0.839587   0.858311   0.007754  -0.000092   
96  108.293435  8.293435  6.347401   6.022254   0.381717  -0.031700   
97  102.161766  2.161766  1.568848   1.569761   0.025935  -0.000561   
98   94.516163 -5.483837 -3.832520  -3.982073   0.166894   0.009164   
99   99.493932 -0.506068 -0.392564  -0.367480   0.001421   0.000007   

    theta_fac   residue  delta_hedge_residue  
0    -0.02646  0.000193             0.003144  
1    -0.02646 -0.000038            -0.026107  
2    -0.02646  0.000091            -0.016109  
3    -0.02646  0.000061             0.269673  
4    -0.02646  0.000084             0.298552  
..        ...       ...                  ...  
95   -0.02646  0.000074            -0.018724  
96   -0.02646  0.001590             0.325147  
97   -0.02646  0.000174            -0.000912  
98   -0.02646 -0.000046             0.149553  
99   -0.02646 -0.000052            -0.025084  

[100 rows x 9 columns]
average of delta hedge error is 0.2184
average of approximation error is 0.0005
spot                   99.849576
ds                     -0.150424
dc                      0.109175
delta_fac              -0.109230
gamma_fac               0.243649
speed_fac               0.000684
theta_fac              -0.026460
residue                 0.000532
delta_hedge_residue     0.218405
dtype: float64

Process finished with exit code 0

 

델타헤지만 했을 때 콜옵션 가격의 변화를 델타 매매(기초자산 매매)로 커버하고 남는 수준이 약 0.22 정도 됩니다 (결과 중간의 average of delta hedge error 참고) 

이 값은 call option 가격 변화에서, 델타 헤지분 (delta_fac)의 성과만 제외한 값이죠.

 

그런데 만일 모든 민감도 팩터 (세타, 감마, 스피드까지!)를 헤지를 통해 제거할 수만 있다면! 근삿값 차이가 0.0005까지 떨어질 정도로 헤지 성과를 보이죠. 다른 말로 하자면

 

 

델타 외 다른 민감도도 헤지할 수단만 있다면, 다 헤지해 버려서 콜옵션 가격을 타이트하게 좇을 수 있다!!

 

 

입니다. 델타야 기초자산을 샀다 팔았다 하면 되고, 감마나 스피드, 세타까지 헤지 도구로 쓸 물건만 있다면 콜옵션 움직임을 완전 복제할 수 있다는 이야기죠.

 

만일 그렇지 않더라도, 콜옵션의 움직임 중 어떤 팩터는 헤지가 되는 부분이고, 또 어떤 부분은 헤지가 안 되는 영역인지를 알아볼 수 있으니 더 좋은 상황인 것입니다.

 

 

이번 글을 통해, 콜옵션의 움직임을 세타와 기초자산 민감도(델타, 감마, 스피드)로 헤지할 수 있음을 알았습니다.

그러면 콜옵션의 움직임에 영향을 주는 다른 요인은 없을까요?

 

위 코드의 콜옵션 공식을 보시죠.

def CallOptionBS(S, K, T, r, q, sigma):

 

$S, T$에 대해서는 이미 알아봤습니다. 사실 $T$는 콜옵션의 만기라 상수일 것 같지만, 식을 자세히 들여다보면 "잔존만기"라는 뜻임을 알 수 있습니다. 즉 콜옵션 만기를 $T$, 콜옵션의 계산시점을 $t$라 했을 때,

$$T-t$$ 대신 $T$로 보기 좋게 코딩한 것일 뿐이죠. 따라서 위 공식의 $T$도 상수가 아닌 변수입니다.

 

$K$는 행사가로서 누가 봐도 상수이죠. 얘에 대해서는 민감도가 발생하질 않습니다. 문제는

$$ r, q, \sigma$$

라는 변수이죠. 각각 무위험 이자율,  배당률 그리고 변동성입니다.

 

얘네들은 시장 상황에 따라 바뀌는 변수이죠. 따라서 민감도가 발생합니다. 

 

 

다음 글에서는 변동성, 이자율 등 콜옵션 가격을 구할 때 투입되는 변수들에 대한 민감도에 대해 알아보겠습니다.