이번 글은 콜옵션의 가격 변화를 쫓아가보자 #2
콜옵션의 가격 변화를 쫓아가보자 #2
이 글은 콜옵션의 가격 변화를 쫓아가보자 #1 콜옵션의 가격 변화를 쫓아가보자 #1 이 글은 테일러 전개 : 파생상품 헤지의 준비 이론 테일러 전개 : 파생상품 헤지의 준비 이론 이 글은 예전글인
sine-qua-none.tistory.com
에서 이어집니다.
시점 $t$에서 기초자산 현재가가 $S$에서 $S+\Delta S$로 변했을 때, 콜옵션 가격 $c(t,S)$의 변화는 근사적으로
$$ c(t,S+\Delta S) - c(t,S) \approx \frac{\partial c(t,S)}{\partial S} \cdot \Delta S \tag{1}$$
로 주어집니다.
콜옵션 가격은 기초자산 $S$의 움직임에 영향을 많이 받습니다. 문제는, $S$가 어디로(위? 아래?) 움직일지 몰라 이게 바로 리스크라는 것이죠.
물론 콜옵션 매수자들은 기초자산이 오르길 희망하고, 콜옵션 매도자들은 기초자산이 떨어지길 희망할 것입니다. 하지만 이건 방향성을 예측하여 투자하는 투자자들의 행태이죠. 분명히 콜옵션 기초자산의 움직임으로부터 자유롭고 싶은 투자자들도 있을 것입니다.
이번 글의 주제는
과연 콜옵션 투자를 기초자산 변동의 위험에서 어떻게 구출해 낼 수 있을까?
입니다.
상황 예시: 콜옵션 매도 투자자의 헷징 기법
콜옵션 매도 투자자가 있습니다. 기초자산이 오를 때는 콜옵션 가격이 올라, 이 투자는 손실이 나죠(매도한 파생상품의 가격이 오르면 나중에 비싸게 사서 거래상대방한테 페이오프를 챙겨줘야 하므로 손실.) 반면, 기초자산이 내리면, 콜옵션 가격은 떨어져 이익이 납니다(나중에 싸게 사서 거래상대방에게 페이오프를 줄 수 있기 때문)
그럼 위의 투자자는 어떤 물건을 같이 들고 있어야 기초자산 변동에 따른 위험을 막을 수 있을까요?
바로 위의 보라색으로 설명한 상품입니다. 기초자산 상승 시 이익이 나고, 하락 시에는 손실이 발생해서 각각의 상황에 발생하는 콜옵션 손익을 어느 정도 벌충할 수 있죠.
그렇다면, 기초자산이 상승할 때 수익이 나고, 하락할 때 손실이 발생하는 대표적인 상품은 뭐가 있을까요? 바로
기초자산 그 자체! 를 매수 포지션으로!
입니다.
그렇다면, 또 한 가지 의문이 생깁니다. 과연 기초자산 몇 주를 들고 있어야 할까요? 그래야 제대로 콜옵션 매도의 손실/이익과 퉁쳐질까요? 정답은 식 (1)에 있습니다.
콜옵션 매도 투자위험을 퉁칠만한 기초자산 수량은?
콜옵션을 하루 한 번씩 정산한다 하고, 현재시점부터 만기 $T$ 시점까지 daily 시점을
$$ 0=t_0 <t_1<\cdots< t_{N-1}=t_N=T$$ 라 합시다. 시점 $t_i$에서 결정된 기초자산 주식의 가격은 $S_i$라 합시다.
그렇다면 시점 $t_i$, $t_{i+1}$사이에 발생하는 콜옵션 매도 포지션의 손익은
$$ c(t_i , S_i) - c(t_{i+1}, S_{i+1}) $$ 입니다.
반면 기초자산 1개에서 발생하는 평가손익은
$$ S_{i+1}-S_{i}$$
입니다.
특별히 시점 $t_i$에서 $$\frac{\partial c(t_i,S_i)}{\partial S}$$개의 기초자산을 보유하고 있다고 해보겠습니다. 이게 바로 시점 $t_i$에서의 콜옵션의 델타이죠
이를 time line으로 설명하면 다음과 같습니다. 임의의 $i$에 대해
| 시점 | 기초자산보유수량 | 기초자산 | 1 unit 콜옵션 매도 |
| $t_i$ | $\frac{\partial c(t_i,S_i)}{\partial S}$ | $S_i$ | $-c(t_i,S_i)$ |
| $t_{i+1}$ | $S_{i+1}$ | $-c(t_{i+1},S_{i+1})$ | |
| 손익 | $\frac{\partial c(t_i,S_i)}{\partial S} (S_{i+1}-S_i)$ | $c(t_i,S_i)-c(t_{i+1},S_{i+1})\tag{2}$ |
여기서, 이 글에서는 일단 $t_i$와 $t_{i+1}$ 사이에 시간 변화를 우선 고려해 보지 말기로 합시다. 무슨 뜻이냐면, 위의 표 안의 식 (2)에서,
$$
\begin{align}
c(t_i,S_i)-c(t_{i+1},S_{i+1}) & = c(t_i,S_i)-c(t_i,S_{i+1}) +c(t_i,S_{i+1})-c(t_{i+1},S_{i+1}) \\
& = c(t_i,S_i)-c(t_i,S_{i+1}) +\text{시점 변화에 따른 량} \tag{3}
\end{align}
$$
위에서 시점 변화에 따른 량은 일시적으로 무시해 보도록 하죠. 이것이 바로 나중에 설명할 "옵션의 세타"입니다.
자, 그럼 식 (2)은
$$ c(t_i,S_i)-c(t_i,S_{i+1}) $$ 라고 일단 일시적으로 생각해 보면,
식(1)에 의해
$$ c(t_i,S_i)-c(t_i,S_{i+1}) + \frac{\partial c(t_i,S_i)}{\partial S} (S_{i+1}-S_{i}) \approx 0$$
입니다.
즉,
콜옵션 매도 포지션에서 발생하는 일일 평가 손익이
기초자산을 $\frac{\partial c}{\partial S}$ 개 만큼, 즉, 델타만큼 가지고 있으니
헷지(hedge)가 되는구나!
라는 사실입니다. 이론적인 배경을 알아봤으니,
콜옵션 매도 포지션을 기초자산 델타 개로 헤지 하는 모습을
코딩해 보겠습니다.
Python Code : 콜옵션 매도 포지션의 헷징
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# call option value, delta, gamma, speed function
def CallOptionBS(S, K, T, r, q, sigma):
Ncdf = norm.cdf
npdf = norm.pdf
if T == 0:
val = np.maximum(S - K, 0)
delta = 1 if S >= K else 0
gamma = 0
speed = 0
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
val = S * np.exp(-q * T) * Ncdf(d1) - K * np.exp(-r * T) * Ncdf(d2)
delta = np.exp(-q * T) * Ncdf(d1)
gamma = np.exp(-q * T) * npdf(d1) / (S * sigma * np.sqrt(T))
speed = -np.exp(-q * T) * npdf(d1) / (S ** 2 * sigma * np.sqrt(T)) * (1 + d1 / (sigma * np.sqrt(T)))
return val, delta, gamma, speed
# -----------------------------------------------------------
# call option short position 을 기초자산으로 hedging 하는 test
# -----------------------------------------------------------
def call_option_hedge_test():
s0 = 100 # 기초자산 현재가
strike = 100 # 행사가 strike
maturity = 1 # 만기
rfr = 0.03 # 무위험 이자율
div = 0 # 연속배당률
vol = 0.3 # 변동성
dt = 1 / 250 # 1일을 의미 (1y= 250일)
sqrtdt = np.sqrt(dt)
ntime = int(maturity / dt) # time grid 개수
time_series = np.linspace(0, maturity, ntime + 1) # t_0 <t_1<...<t_N , t_i=(1/25)i
ttm_series = np.flip(time_series) # 잔존만기를 위해 flip을 써서 reversed array 만듬
drift = rfr - div - 0.5 * vol ** 2 # GBM process의 drift
spot_series = [s0] # 우선 spot array는 현재가 부터 시작
dailyspot = s0
for _ in range(len(time_series) - 1):
# GBM으로 일간 주가 path 생성
dailyspot *= np.exp(drift * dt + vol * sqrtdt * np.random.normal())
spot_series.append(dailyspot)
callval_series = [] # 일간 call option value 저장할 list
calldelta_series = [] # 일간 call option delta 저장할 list
for ttm, spot in zip(ttm_series, spot_series): #(잔존만기, 주가패스) 에 대해
call_info = CallOptionBS(spot, strike, ttm, rfr, div, vol) # call value 정보 추출
callval_series.append(call_info[0]) # 0번째 값은 value
calldelta_series.append(call_info[1]) # 1번째 값은 delta
# diff 함수를 써서 call option value 원소간 차이를 구함
# 매도포지션이므로 -1을 곱해줌
short_call_pl = np.diff(np.array(callval_series)) * -1
# i번째 delta : t_i 시점에 보유할 기초자산의 갯수
# 거기에 S_{i+1}-S_i 즉, 기초자산의 변동을 곱해줘 기초자산 손익을 구함
long_spot_pl = np.diff(np.array(spot_series)) * np.array(calldelta_series)[:-1]
# call 매도와 기초자산 보유에서 발생하는 손익의 net 손익을 구함
net_pl = short_call_pl + long_spot_pl
fig, ax = plt.subplots(2, 1, figsize=(20, 20))
# ax[0] 에 call value 와 기초자산의 가격 변화를 plotting
# strike 도 hline 함수를 사용하여 표시
ax[0].plot(time_series, callval_series, linewidth=2, color='black', label='Black Scholes Formula value')
ax[0].legend(loc='lower left')
ax0 = ax[0].twinx()
ax0.plot(time_series, spot_series, label='underlying process', color='blue')
ax0.hlines(strike, xmin=time_series[0], xmax=time_series[-1], label='strike', color='green')
ax0.legend()
# ax[1] 에 call option delta 의 변화도 plotting
ax[1].plot(time_series, calldelta_series, label='delta')
ax[1].legend()
# grid를 이용하여 멋진 graph를 그림
from matplotlib import gridspec
fig = plt.figure(figsize=(20, 20))
# 2*1 차트를 그리는데, 위의 차트와 아래 차트 크기 비율을 3:1로
gs = gridspec.GridSpec(nrows=2, ncols=1, height_ratios=[3, 1])
ax = [fig.add_subplot(gs[0]), fig.add_subplot(gs[1])]
# ax[0] 에 net 손익은 plotting으로
# call 매도 포지션 손익과 기초자산에서 발생하는 손익은 각각 bar 차트로 그림
ax[0].plot(time_series[1:], net_pl, linewidth= 3, label='net daily p&l', color='red')
ax[0].bar(time_series[1:], short_call_pl, width=1 / 500, label='short call pl', alpha=0.6)
ax[0].bar(time_series[1:], long_spot_pl, width=1 / 500, label='long stock p&l', alpha=0.6)
ax[0].legend()
# cumsum() 함수를 이용하여 누적 손익을 구함(daily 손익을 누적해서 그리면 총 손익이 되므로)
# index -1 을 사용하면 전체 누적 손익을 구할 수 있음
total_pl = round(net_pl.cumsum()[-1], 2)
# ax[1] 에 net 손익을 plotting
# total 손익을 점으로 크게 찍고, texting 함
ax[1].plot(time_series[1:], net_pl.cumsum(), color='blue', label='accumulated p&l')
ax[1].scatter(time_series[-1], total_pl, s=50, color='blue')
ax[1].text(time_series[-10], total_pl * 0.8, f'P&L={total_pl}')
ax[1].legend(loc='upper left')
# 위의 그림 2개 동시에 띄움
plt.show()
def call_option_approximation_test():
s0 = 100
K = 100
T = 1
rfr = 0.03
q = 0
sigma = 0.3
rate_vec = np.linspace(-0.9, 0.9, 100 + 1)
s_vec = s0 * (1 + rate_vec)
call_value_ftn = lambda s: CallOptionBS(s, K, T, rfr, q, sigma)[0]
call_value_vec = np.array([call_value_ftn(s) for s in s_vec])
val0, delta0, gamma0, speed0 = CallOptionBS(s0, K, T, rfr, q, sigma)
ds_vec = s_vec - s0
first_aprx_vec = val0 + delta0 * ds_vec
second_aprx_vec = first_aprx_vec + 0.5 * gamma0 * ds_vec ** 2
third_aprx_vec = second_aprx_vec + (1 / 6) * speed0 * ds_vec ** 3
fig, ax = plt.subplots(2, 2, figsize=(20, 20))
ax[0, 0].plot(s_vec, call_value_vec, linewidth=2, color='black', label='Black Scholes Formula value')
ax[0, 0].legend()
ax[0, 1].plot(s_vec, first_aprx_vec, label='1st approx', color='blue')
ax[0, 1].plot(s_vec, call_value_vec, linewidth=2, color='black', label='Black Scholes Formula value')
ax[0, 1].fill_between(s_vec, call_value_vec, first_aprx_vec, color='lightgray', alpha=0.8, label='error area')
ax[0, 1].legend()
ax[1, 0].plot(s_vec, second_aprx_vec, label='2nd approx', color='green')
ax[1, 0].plot(s_vec, call_value_vec, linewidth=2, color='black', label='Black Scholes Formula value')
ax[1, 0].fill_between(s_vec, call_value_vec, second_aprx_vec, color='lightgray', alpha=0.8, label='error area')
ax[1, 0].legend()
ax[1, 1].plot(s_vec, third_aprx_vec, label='3rd approx', color='red')
ax[1, 1].plot(s_vec, call_value_vec, linewidth=2, color='black', label='Black Scholes Formula value')
ax[1, 1].fill_between(s_vec, call_value_vec, third_aprx_vec, color='lightgray', alpha=0.8, label='error area')
ax[1, 1].legend()
plt.show()
# plt.plot(s_vec, call_option_value)
# plt.show()
# print(s_vec)
if __name__ == '__main__':
call_option_hedge_test()
자세한 사항은 주석을 참고하시기 바랍니다. 참고로
○ numpy.flip : array 배열을 역으로 정렬하는 함수
○ numpy.diff : array 원소 간 차이를 계산하는 함수 ( size는 하나 줄어든다.)
○ numpy.cumsum : array의 원소를 누적 합산하는 함수
의 numpy 함수를 써서 코딩하였습니다.
결과를 볼까요? random seed를 고정하지 않아, 시뮬레이션할 때마다 결과가 바뀌는 것을 볼 수 있습니다. 이중
행사가와 만기 시 주가를 비교하여 각각의 경우에 대해 알아보도록 합시다.
만기시 주가가 행사가보다 위에서 끝나는 경우
이 때는 콜옵션 가격이 통통히 살게 되죠. ITM으로 끝났으니깐요.
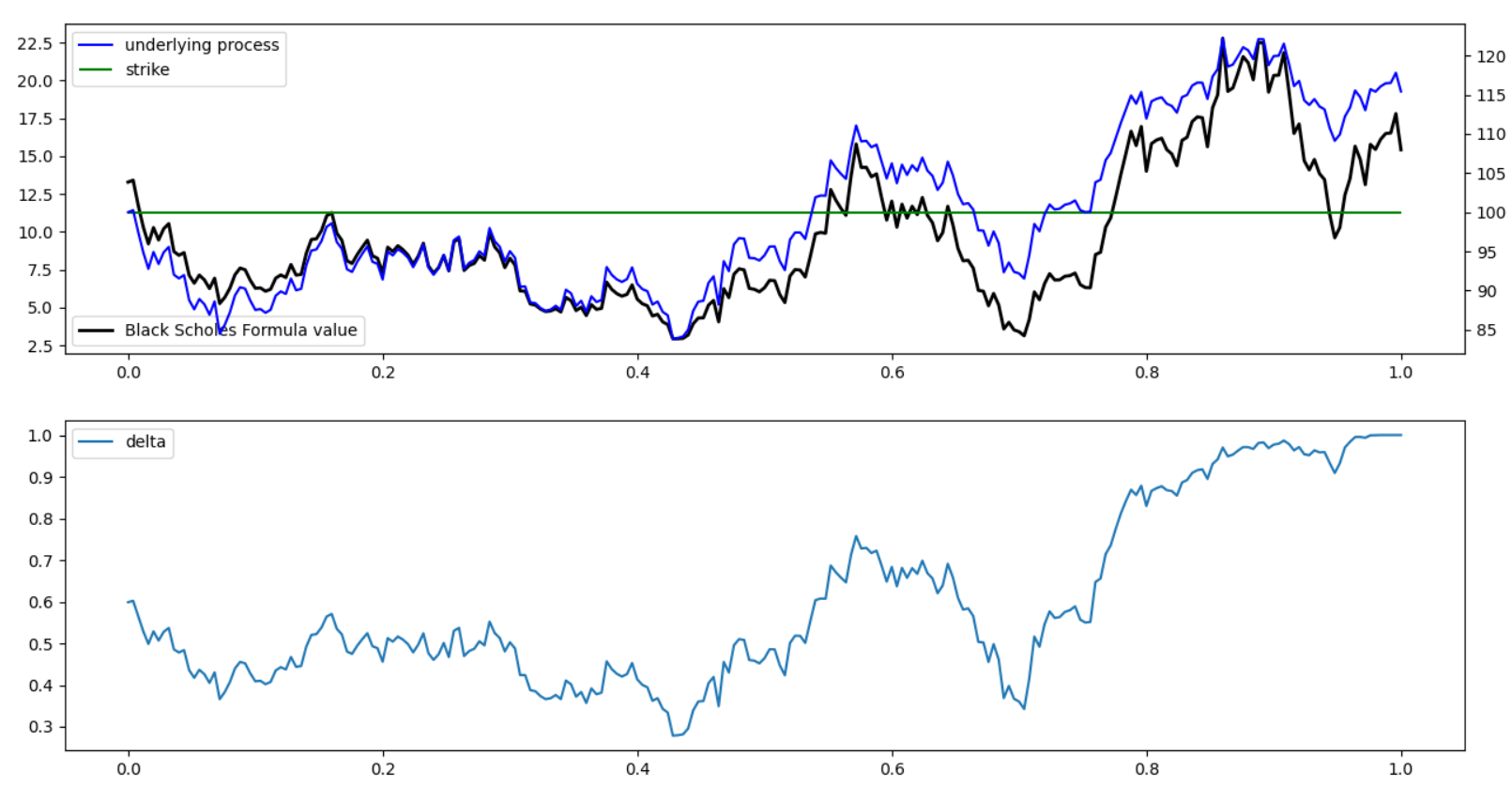
1. 첫 번째 그림은 주가가 행사가 위에서 끝났음을 보여줍니다. 콜옵션 가격 역시 만기 주가와 행사가의 차이(ITM)로 살아 있게 되죠.
2. 두 번째 그림은 델타 그래프입니다. 만기로 갈수록 콜옵션 가격이 $S-K$ 형태의 함수를 보이기 때문에 $S$로 미분한 델타는 1로 수렴하게 됩니다.
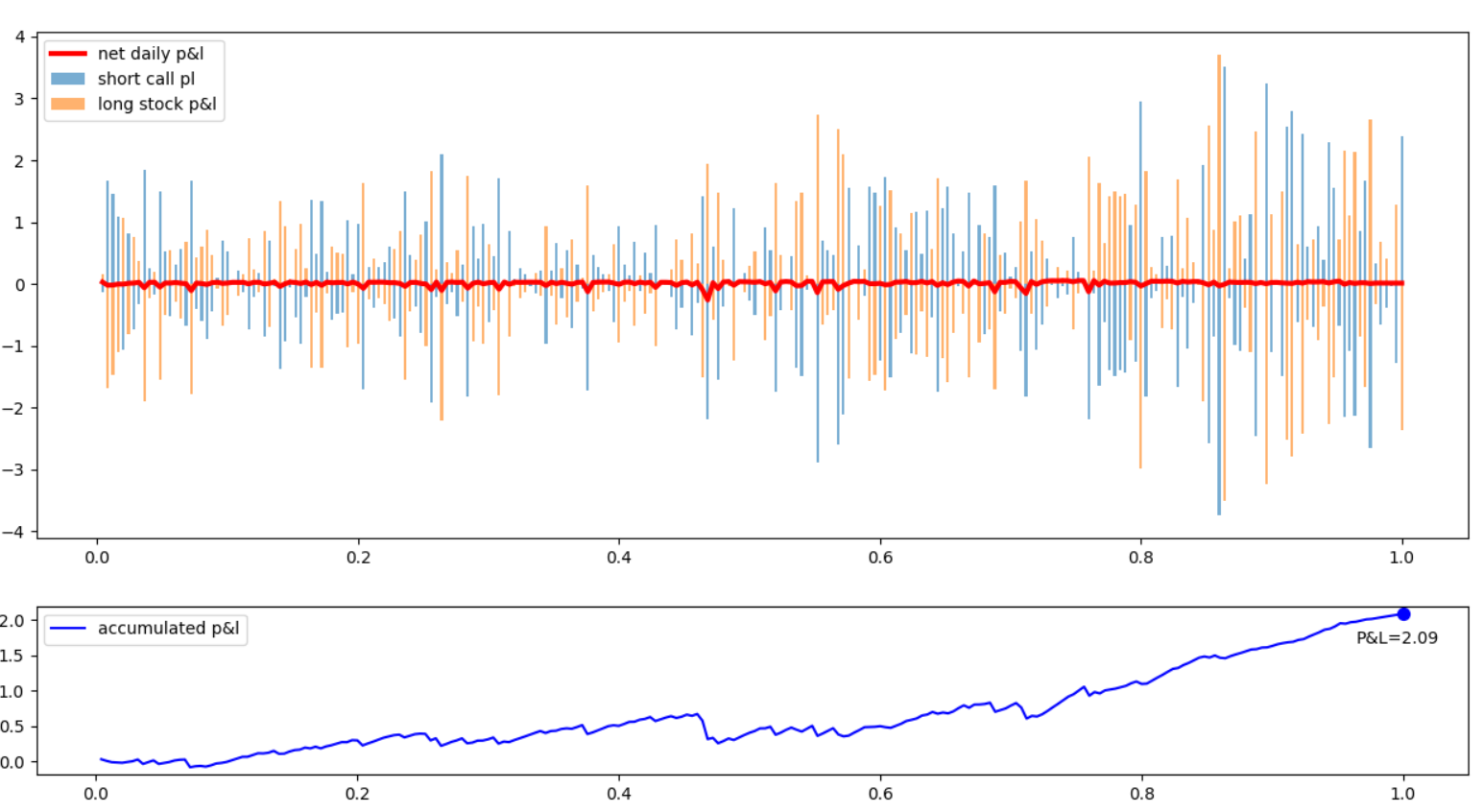
3. 세 번째 그림은 콜옵션 매도에서 발생하는 일일 손익(파란색)과 , 기초자산에서 발생하는 일일수익(주황색), 또 이 둘을 합친 상계(net) 손익(빨간색)을 그린 것입니다. 처음 며칠을 확대해 보면, 파란색과 주황색 막대가 반대방향을 향하고 있음을 알 수 있죠. 즉, 콜옵션 매도에서 수익이 나면 기초자산 보유에서 손실이 나고, 그 역도 마찬가지입니다. 따라서 상계를 치면 빨간색 그래프처럼 잔잔하게 0에 붙어있는 그림이 나오죠.
4. 네 번째 그림은 누적 손익입니다. 기초자산 변동에 따른 위험을 제거하면서 일일 수익을 쌓아봤더니 제법 괜찮게도 우상향 하는 손익이 나오네요. 토털 얻은 수익은 2.09입니다(기초자산 100에 대한 비율)
이제 콜옵션이 꽝 되는 경우인 아래를 살펴보죠.
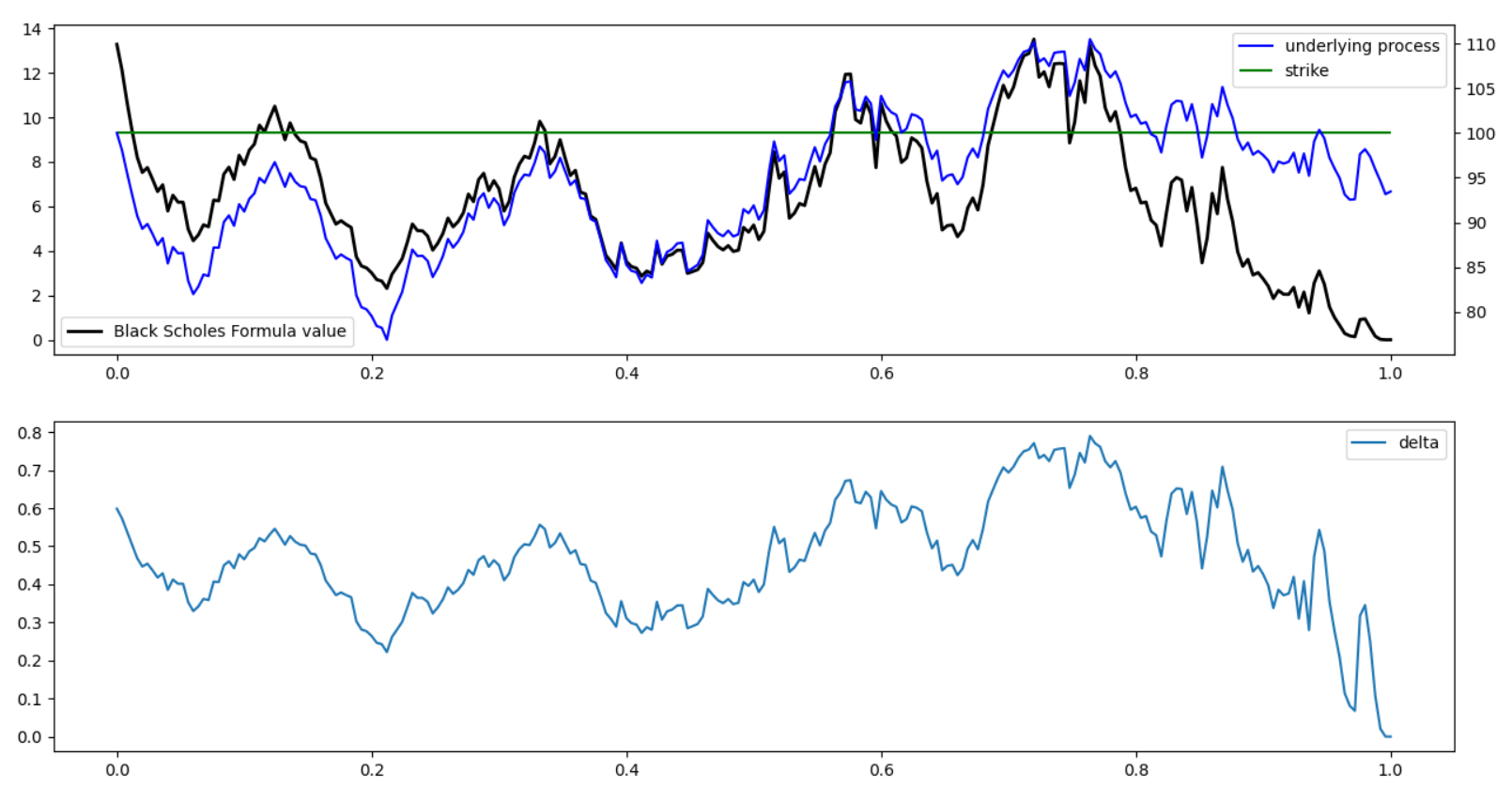
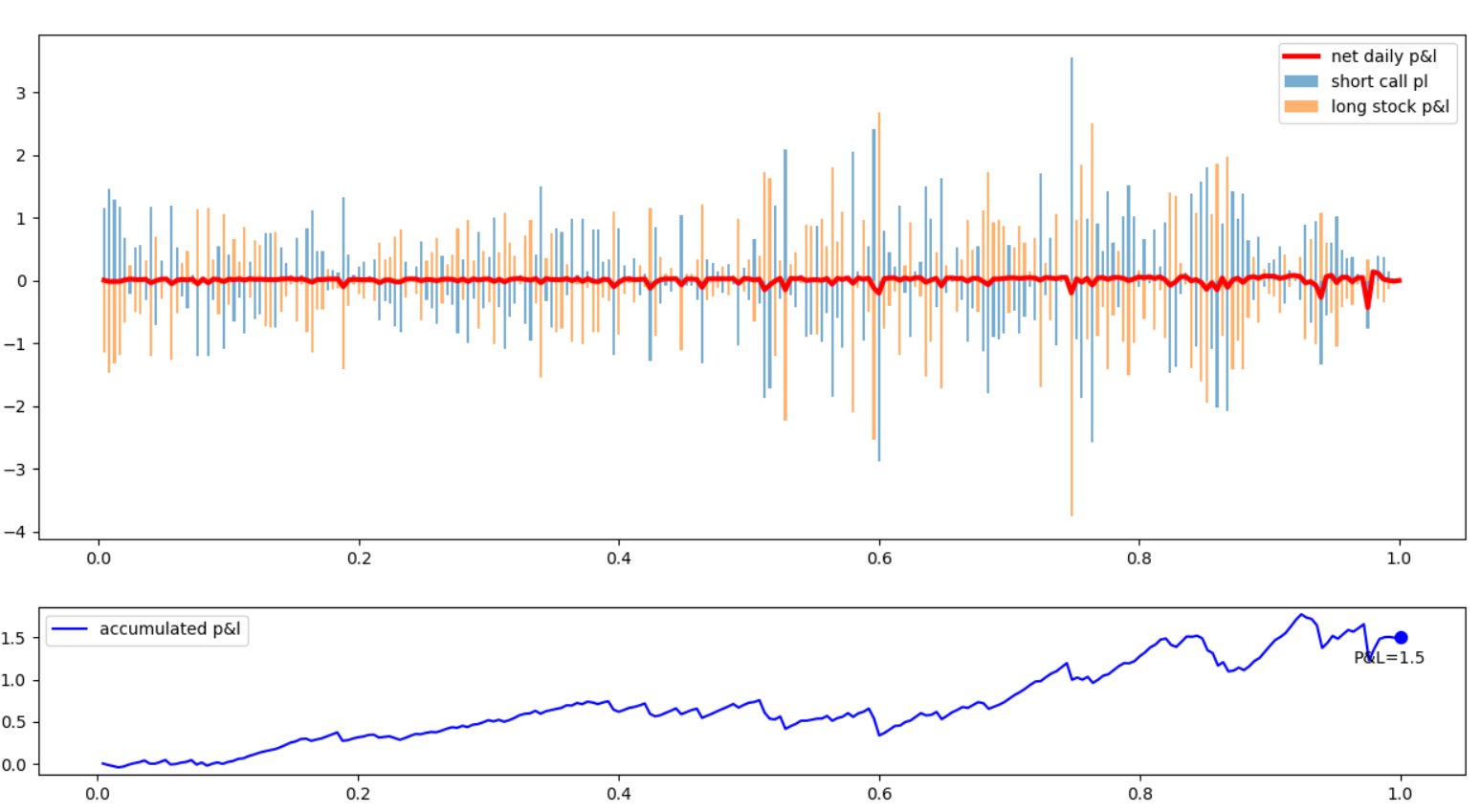
만기 시 주가가 행사가보다 아래에서 끝나는 경우
이 때도 결과는 비슷합니다. 다만, 주가가 행사가를 하회하면 콜옵션 가격은 0으로 가고, 델타 역시 0으로 가죠. 마찬가지로 콜옵션 매도 일일수익과 기초자산 일일수익은 서로 반대 방향으로 상계하면 0에 근사합니다. 누적 손익은 쌓여 1.5 정도 기록하는 상황이네요.
더 알아볼 것은?
옵션의 가격변화를 기초자산으로 트레킹 하여 헤지할 수 있다는 것을 위의 예제를 통해 알아봤는데요. 우리는 여기서 한 가지 가정한 것이 있습니다. 바로
식(3)의 "시간에 따른 변화량"을 대놓고 무시했다는 사실
이죠. 콜옵션 가격은 시점 $t$와 기초자산 $S$, 두 변수의 함수로 만들어졌기 때문에 시간에 따른 변화량도 엄연히 존재합니다. 이 변화량을 감안해야 비로소 더욱더 그럴싸한 헷지 방법이 되겠죠.
미리 소개하자면, 시간의 따른 변화량을 세타(Theta , $\Theta$)라 합니다. 역시 그리스 문자(Greeks)이죠. 다음 글에서 자세히 알아보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 콜옵션 좀 복제해줘~ (0) | 2023.05.10 |
|---|---|
| 콜옵션 가격 변동 헤지(hedge) 시뮬레이션 (0) | 2023.05.09 |
| 델타, 감마, 스피드! 콜옵션의 가격 변화를 쫓아가보자 #2 (0) | 2023.05.03 |
| 델타, 감마, 스피드! 콜옵션의 가격 변화를 쫓아가보자 #1 (0) | 2023.04.27 |
| 퀀토 상품 모델링 (0) | 2023.04.21 |
댓글