델타, 감마, 스피드! 콜옵션의 가격 변화를 쫓아가보자 #2

728x90

콜옵션의 가격 변화를 쫓아가보자 #1

이 글은 테일러 전개 : 파생상품 헤지의 준비 이론 테일러 전개 : 파생상품 헤지의 준비 이론 이 글은 예전글인 2022.05.19 - [수학의 재미/아름다운 이론] - 테일러 전개 #1 테일러 전개 #1 무한번 미

sine-qua-none.tistory.com

에서 이어집니다. 우선 지난 글에서 다루었던 내용을 복습해 보자면,

콜옵션의 델타, 감마, 스피드

기초자산 가격의 변화에 따라 콜옵션의 가격이 변하는 정도를 다음과 같이 구할 수 있습니다.

: 기초자산( $S$ )에 대한 1계 미분값

: 기초자산( $S$ )에 대한 2계 미분값

스피드(Speed): 기초자산( $S$ )에 대한 3계 미분값

3차 미분으로 갈수록 그 값이 작아지고, 영향도가 떨어져서 델타, 감마 같은 별칭이 없습니다만, 2차 미분값까지는 델타( $\Delta$ ), 감마( $\Gamma$ )처럼 그리스 문자(Greeks)로 불리는 별칭이 있습니다.

그 값들을 표로 정리해 보면 아래와 같습니다.

그릭(Greeks)	수식
델타, $\Delta$	$e^{-q(T-t)} \Phi(d_1)$
감마, $\Gamma$	$\frac{e^{-q(T-t)} \phi(d_1) }{S\sigma \sqrt{T-t}}$
스피드	$- \frac{e^{-q(T-t)} \phi(d_1)}{S^2\sigma\sqrt{T-t}} \left[ 1+\frac{d_1}{\sigma\sqrt{T-t}} \right]$

참고로 콜옵션의 가격 구하는 공식은 Black Scholes Formula는 다음과 같죠.

$c(t,S) = S e^{-q(T-t)} \Phi(d_1) - Ke^{-r(T-t)}\Phi(d_2)\tag{3}$

$d_1 = \frac{\ln(S/K)+(r-q+\textstyle{\frac12}\sigma^2)(T-t)}{\sigma\sqrt{T-t}}~~,~~ d_2= d_1-\sigma\sqrt{T-t} \tag{4}$

위의 공식에서 $\Phi(\cdot), \phi(\cdot)$ 는 각각 표준정규분포의 cdf, pdf입니다.

이제 델타, 감마, 스피드 값을 가지고 콜옵션 가격의 변화를 추정해 보는 테스트를 파이썬 코딩을 통해 알아보겠습니다.

Python Code : 민감도로 콜옵션 변화 추적해 보기

기초자산의 현재 가격 $S_0 =100$ 이고, 이 기초자산이 -40% 하락에서부터 40% 상승까지, 즉,

$60 \leq S \leq 140$

사이에서 변할 때, 콜옵션 가격도 변할 것입니다. 이 변하는 값을

1. $S_0$ 에서의 콜옵션의 가격과

2. $S_0$ 에서의 이 콜옵션의 델타, 감마, 스피드

를 이용해서 추정해 보도록 하겠습니다. 추정 방법은 앞선 글(테일러 전개 : 파생상품 헤지의 준비 이론)에서 소개한 바 있습니다. 이 글을 콜옵션의 상황에 맞게 수식으로 써보면 아래와 같습니다.

$c(t,S) -c(t,S_0) \approx \frac{\partial c(t,S_0)}{\partial S} (\Delta S) + \frac{\partial^2 c(t,S_0)}{\partial S^2} (\Delta S)^2 +\frac{\partial^3 c(t,S_0)}{\partial S^3} (\Delta S)^3 ,$

여기서 $\Delta S = S-S_0$ 임

(눈치채셨겠지만, 시점에 대한 변수 $t$ 는 고정시켜 놓고 마치 상수처럼 취급하여 테일러 전개를 한 것입니다.)

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm


def CallOptionBS(S, K, T, r, q, sigma):
    Ncdf = norm.cdf       # standard normal distribution의 cdf
    npdf = norm.pdf       # standard normal distribution의 pdf

    if T == 0:            # 잔존만기가 0일 때, 즉 만기시점
        val = np.max(S - K, 0)
        delta = 1 if S >= K else 0
        gamma = 0
        speed = 0
    else:
        d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
        d2 = d1 - sigma * np.sqrt(T)
        val = S * np.exp(-q * T) * Ncdf(d1) - K * np.exp(-r * T) * Ncdf(d2)  # call option value
        delta = np.exp(-q * T) * Ncdf(d1)                              # call option delta
        gamma = np.exp(-q * T) * npdf(d1) / (S * sigma * np.sqrt(T))   # call option gamma
        speed = -np.exp(-q * T) * npdf(d1) / (S ** 2 * sigma * np.sqrt(T)) * (1 + d1 / (sigma * np.sqrt(T)))
                                                                       # call option speed

    return val, delta, gamma, speed   # value 및 3개의 민감도를  return


def call_option_approximation_test():
    s0 = 100     # 현재가
    K = 100      # 행사가, 이 상황에서는 S0=K이므로 ATM인 상황
    T = 1        # 잔존만기 1y
    rfr = 0.03   # risk free rate = 3%
    q = 0        # dividend yield
    sigma = 0.3  # volatility(변동성)

    rate_vec = np.linspace(-0.4, 0.4, 100 + 1)  # 등락률 vector : -40% ~ 40%
    s_vec = s0 * (1 + rate_vec)                 # 등락률을 S0에 곱해 현재가 범위를 만듬
    call_value_ftn = lambda s: CallOptionBS(s, K, T, rfr, q, sigma)[0]  #value 뽑는 lambda 함수
    call_value_vec = np.array([call_value_ftn(s) for s in s_vec])    # 각 기초자산가격에 대한 call value

    val0, delta0, gamma0, speed0 = CallOptionBS(s0, K, T, rfr, q, sigma)  
                                                # S0 시점의 delta, gamma, speed

    ds_vec = s_vec - s0       # 현재가와 기준가(S0=100)의 차이, 즉 ΔS 구함
    first_aprx_vec = val0 + delta0 * ds_vec    # 테일러 전개의 1차 근사(delta 까지!)
    second_aprx_vec = first_aprx_vec + 0.5 * gamma0 * ds_vec ** 2
                                               # 테일러 전개의 2차 근사(gamma 까지!)
    third_aprx_vec = second_aprx_vec + (1 / 6) * speed0 * ds_vec ** 3
                                               # 테일러 전개의 3차 근사(speed 까지!)

    fig, ax = plt.subplots(2, 2, figsize=(20, 20))
    #call value graph
    ax[0, 0].plot(s_vec, call_value_vec, linewidth=2, color='black', label='Black Scholes Formula value')
    ax[0, 0].legend()
    
    # call value를 1차 근사식으로 구하기
    ax[0, 1].plot(s_vec, first_aprx_vec, label='1st approx', color='blue')
    ax[0, 1].plot(s_vec, call_value_vec, linewidth=2, color='black', label='Black Scholes Formula value')
    ax[0, 1].fill_between(s_vec, call_value_vec, first_aprx_vec, color='lightgray', alpha=0.8, label='error area')
    ax[0, 1].legend()
    
    # call value를 2차 근사식으로 구한 graph
    ax[1, 0].plot(s_vec, second_aprx_vec, label='2nd approx', color='green')
    ax[1, 0].plot(s_vec, call_value_vec, linewidth=2, color='black', label='Black Scholes Formula value')
    ax[1, 0].fill_between(s_vec, call_value_vec, second_aprx_vec, color='lightgray', alpha=0.8, label='error area')
    ax[1, 0].legend()
    
    # call value를 3차 근사식으로 구한 graph
    ax[1, 1].plot(s_vec, third_aprx_vec, label='3rd approx', color='red')
    ax[1, 1].plot(s_vec, call_value_vec, linewidth=2, color='black', label='Black Scholes Formula value')
    ax[1, 1].fill_between(s_vec, call_value_vec, third_aprx_vec, color='lightgray', alpha=0.8, label='error area')
    ax[1, 1].legend()

    plt.show()

if __name__ == '__main__':
    call_option_approximation_test()

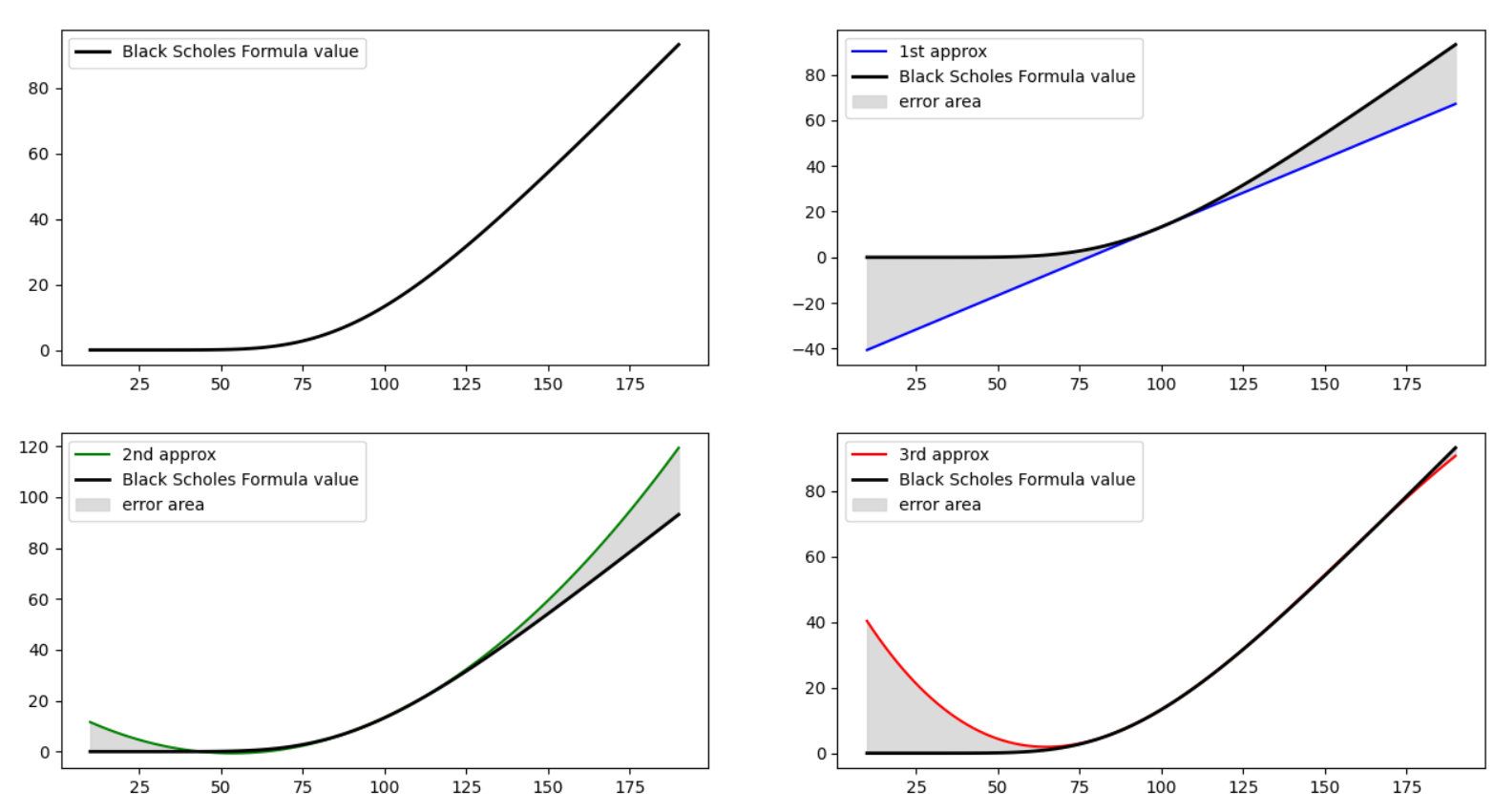
이제 결과를 보겠습니다.

○ 좌측 상단의 그래프는 우리에게 익숙한 콜옵션 그래프입니다(검은색)

○ 우측 상단은 $c(t,S_0)$ 와 델타만 가지고 콜옵션 가격을 추정해 본 것입니다(파란색 선.)

1차 근사식은 $\Delta S$ 에 대한 1차식이므로 파란색 선처럼 직선이 나오죠. 기존 콜옵션 가격과의 이격이 제법 납니다(음영 처리 된 부분)

○ 좌측 하단은 $c(t,S_0)$ 와 델타, 감마를 가지고 콜옵션 가격을 추정해 본 것입니다(녹색 선.)

2차 근사식은 $\Delta S$ 에 대한 2차식이고, 녹색 선처럼 2차 곡선이 나오죠. 기존 콜옵션 가격과의 이격이 1차 근사에 비해 매우 줄어들었음을 알 수 있습니다(음영 처리 된 부분)

○ 우측 하단은 $c(t,S_0)$ 와 델타, 감마, 스피드까지 사용하여 콜옵션 가격을 추정해 본 것입니다(빨간 선.)

3차 근사식은 $\Delta S$ 에 대한 3차식이고, 기존 콜옵션 가격과의 이격이 거의 사라짐을 볼 수 있습니다(-40% 하락 부근에서 오차가 발생하긴 하네요.)

이처럼 근사항을 추가할수록 실제값과의 오차가 대폭 줄어들게 됩니다. 다시 말해

공식조차 어려워 보이는 콜옵션 가격을, 델타/감마/스피드를 사용하여 $\Delta S$ 에 대한 다항식으로 추정 가능하다!

라는 것이 요지입니다.

이제 위 코드의 등락률 부분을

    rate_vec = np.linspace(-0.8, 0.8, 100 + 1)

처럼 -80% 하락, 80% 상승으로 바꿔 시뮬레이션을 해 보면 어떨까요? 아래 그림을 보시죠.

아무래도 $\Delta S$ 가 양 사이드 쪽으로 커져서 그런지, 끝단 부근에서는 제대로 근사한 값이 나오지 않는다는 것을 알 수 있습니다.

이는 테일러 전개의 "수렴 반경"이라는 개념과도 연결이 되어 있는데요, 근사식이 성립하기 위해서는 $\Delta S$ 가 허용되는 범위가 존재합니다. 이 범위를 넘어선 값에 대해서는 근사시키가 어려워지요.

하지만, 이런 근삿값은 $Delta S$ 값이 작을 때 주로 사용하죠. 옵션의 기초자산으로 쓰이는 것은 대부분이 KOSPI200, S&P500 등의 지수일 거고, 얘네들의 하루 등락률은 그리 크지 않습니다.

이러한 추정이 필요한 이유?

아니, 기초자산 가격이 변하면, Black Scholes Formula에 대입하여 정확한 옵션 가격을 구하면 되지, 왜 위와 같은 추정이 필요한 걸까요?

주가는 어떻게 변할지 아무도 모릅니다. 즉, 위의 $\Delta S$ 는 불확실한 확률변수이고 이 값은 예상할 수 없으므로 금융에서 흔히 말하는 리스크(RISK)가 되겠죠. 그렇다면, 과연 콜옵션 운용에서 발생하는 리스크는 어찌 될 것인가를 생각해 보면,

$c(t, S+\Delta S) -c(t,S) \approx \frac{\partial c(t,S)}{\partial S} (\Delta S)$

라는 식을 생각해 볼 때,

아! 콜옵션 가격의 변화는, 기초자산 변화의 $\frac{\partial c(t,S)}{\partial S}$ 만큼 되겠구나!

라는 대략의 정보를 얻을 수 있게 된다는 점입니다.

만일 콜옵션 가격의 변화가 두려워 이를 헤지(hedge)하고 싶은 사람은,

콜옵션 한 unit 당 $\frac{\partial c(t,S)}{\partial S}$ 개의 주식을 매도 포지션으로 갖고 있으면 위험이 상쇄된다

는 생각을 하게 될 것입니다. 즉, 파생상품의 위험을 근사적으로라도 정량적으로 구해서, 리스크를 상쇄시킬 대비를 할 수 있는 능력을 가지게 되는 거죠.

이렇듯, 민감도를 산출하고 분석하는 일은 파생상품의 헷지 운용에 키가 되는 아주 중요한 작업입니다.

728x90

'금융공학' 카테고리의 다른 글

콜옵션 가격 변동 헤지(hedge) 시뮬레이션 (0)	2023.05.09
콜옵션 가격 변동 리스크를 없애보자! (0)	2023.05.08
델타, 감마, 스피드! 콜옵션의 가격 변화를 쫓아가보자 #1 (0)	2023.04.27
퀀토 상품 모델링 (0)	2023.04.21
환율은 어떻게 모델링 하나? (0)	2023.04.19

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

Finance Diary

델타, 감마, 스피드! 콜옵션의 가격 변화를 쫓아가보자 #2

콜옵션의 델타, 감마, 스피드

Python Code : 민감도로 콜옵션 변화 추적해 보기

이러한 추정이 필요한 이유?

'금융공학' 카테고리의 다른 글

댓글

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역

델타, 감마, 스피드! 콜옵션의 가격 변화를 쫓아가보자 #2

콜옵션의 델타, 감마, 스피드

Python Code : 민감도로 콜옵션 변화 추적해 보기

이러한 추정이 필요한 이유?

'금융공학' 카테고리의 다른 글

관련글

댓글

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역