이번 글은 저번 글 콜옵션 가격 변동 헤지(hedge) 시뮬레이션
콜옵션 가격 변동 헤지(hedge) 시뮬레이션
이번 글은 콜옵션 가격 변동 리스크를 없애보자! 콜옵션 가격 변동 리스크를 없애보자! 이번 글은 콜옵션의 가격 변화를 쫓아가보자 #2 콜옵션의 가격 변화를 쫓아가보자 #2 이 글은 콜옵션의 가
sine-qua-none.tistory.com
에서 이어집니다.
저번 글에서는 기초자산의 다양한 주가 패스하에서 콜옵션 매도 포지션에 대한 헤지 손익이 어떻게 되는지 알아봤습니다.
저번 글 말미에서
기초자산을 샀다 팔았다 하면서 매매 운용하면 콜옵션 페이오프를 복제해 낼 수 있지 않을까?
라는 질문을 던졌습니다. 콜옵션 매도 포지션이 주식을 샀다 팔았다 하면서 완전 헤지되는 것은, 역으로 말해 주식을 샀다 팔았다 하며 콜옵션 가격의 움직임을 재현해 낸다는 뜻이니까요. 아래의 수식을 보면 명확해집니다.
콜옵션을 복제하다? Replicating!
시간 변화에 따른 콜옵션의 가치 변동성을 제껴 둔 상태애서 기초자산 가격 변동 시, 콜옵션 가격 변동은 아래와 같다고 했습니다.
| c는 콜옵션의 가치, {ti}들은 dialy 시점, Si는 ti 시점의 기초자산 가격이라 합시다. 즉, 콜옵션의 만기 T까지 daily 시점 격자가 0=t0<t1<⋯<tN−1<tN=T 라 주어질 때, c(ti,Si)−c(ti+1,Si+1)+∂c(ti,Si)∂S(Si+1−Si)≈0 |
입니다.
식(1)을 다시 써보면, 모든 시점 index i에 대해,
c(ti+1,Si+1)−c(ti,Si)=∂c(ti,Si)∂S(Si+1−Si)
이고 양변에 ∑N−1i=0 을 취해보면
c(T,ST)−c(0,S0)=N−1∑i=0(c(ti+1,Si+1)−c(ti,Si))≈N−1∑i=0∂c(ti,Si)∂S(Si+1−Si)
입니다. 그런데 c(T,ST)는 만기 때 콜옵션 가치이므로
c(T,ST)=max
이죠(여기서 K는 행사가)
또한 c(0,s_0)는 현재시점의 콜옵션 가격, 즉, 프리미엄입니다.
따라서
\max(S_T-K,0) - c(0,S_0) = \sum_{i=0}^{N-1} \frac{\partial c(t_i,S_i)}{\partial S} (S_{i+1}-S_{i}) \tag{2}
을 만족합니다.
그런데 우변항의 뜻을 가만 보면,
기초자산을 일일 델타만큼 보유함으로써 얻는 자산평가손익
입니다. 즉,
기초자산을 델타 수량만큼 보유하는 전략으로 일일손익을 모두 더해가는 전략으로 콜옵션의 페이오프를 복제할 수 있다!
라는 것이죠. 그럼 이제 코딩을 통해 식(2)이 맞는지 확인을 해 보도록 하겠습니다.
Python Code: 콜옵션 페이오프를 기초자산을 매매하여 복제하기
본 코드는 전의 글(콜옵션 가격 변동 헤지(hedge) 시뮬레이션)의 코드를 그대로 쓸 것입니다. 그리고 살짝 바꿔보도록 하지요. 본 코드는
1. 주가 패스를 500개 생성하여
2. 각 패스에 대해, 콜옵션 일일 델타 수량만큼 기초자산을 샀다 팔았다 한 손익의 누적손익이
3. 콜옵션 페이오프와 모양이 비슷한지 여부
를 관찰하는 것입니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
def CallOptionBS(S, K, T, r, q, sigma):
Ncdf = norm.cdf
npdf = norm.pdf
if T == 0:
val = np.maximum(S - K, 0)
delta = 1 if S >= K else 0
gamma = 0
speed = 0
else:
d1 = (np.log(S / K) + (r - q + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
val = S * np.exp(-q * T) * Ncdf(d1) - K * np.exp(-r * T) * Ncdf(d2)
delta = np.exp(-q * T) * Ncdf(d1)
gamma = np.exp(-q * T) * npdf(d1) / (S * sigma * np.sqrt(T))
speed = -np.exp(-q * T) * npdf(d1) / (S ** 2 * sigma * np.sqrt(T)) * (1 + d1 / (sigma * np.sqrt(T)))
return val, delta, gamma, speed
def call_option_replicating_simulation():
s0 = 100
strike = 100
maturity = 1
rfr = 0.03
div = 0
vol = 0.3
dt = 1 / 250
sqrtdt = np.sqrt(dt)
ntime = int(maturity / dt)
time_series = np.linspace(0, maturity, ntime + 1)
ttm_series = np.flip(time_series)
drift = rfr - div - 0.5 * vol ** 2
final_spot = []
hedge_pl = []
stock_path_example = []
nInteration = 500
for iter in range(nInteration):
spot_series = [s0]
dailyspot = s0
for _ in range(len(time_series) - 1):
dailyspot *= np.exp(drift * dt + vol * sqrtdt * np.random.normal())
spot_series.append(dailyspot)
if iter < 10:
stock_path_example.append(spot_series)
callval_series = []
calldelta_series = []
for ttm, spot in zip(ttm_series, spot_series):
call_info = CallOptionBS(spot, strike, ttm, rfr, div, vol)
callval_series.append(call_info[0])
calldelta_series.append(call_info[1])
short_call_pl = np.diff(np.array(callval_series)) * -1
long_spot_pl = np.diff(np.array(spot_series)) * np.array(calldelta_series)[:-1]
# net_pl = short_call_pl + long_spot_pl
net_pl = long_spot_pl # 이 부분만 바꾼다!
acc_net_pl = net_pl.cumsum()
final_spot.append(spot_series[-1])
hedge_pl.append(acc_net_pl[-1])
spot_vec = np.linspace(50, 150, 100 + 1)
call_payoff = np.maximum(spot_vec - strike, 0)
call_payoff -= callval_series[0]
# hedge_mean = round(np.mean(hedge_pl), 2)
# hedge_std = round(np.std(hedge_pl), 2)
#
# print('hedge p&l mean : {}'.format(hedge_mean))
# print('hedge p&l std : {}'.format(hedge_std))
from matplotlib import gridspec
fig = plt.figure(figsize=(20, 20))
gs = gridspec.GridSpec(nrows=2, ncols=1, height_ratios=[1, 3])
ax = [fig.add_subplot(gs[0]), fig.add_subplot(gs[1])]
for i in range(10):
ax[0].plot(time_series, stock_path_example[i])
ax[0].set_title('stock path example')
ax[1].scatter(final_spot, hedge_pl, label='hedge p&l', color='tomato')
ax[1].plot(spot_vec, call_payoff, label='theoretical call payoff', color='blue')
ax[1].hlines(0, xmin=50, xmax=150, color='gray')
# ax[1].hlines(hedge_mean, xmin=np.min(final_spot), xmax=np.max(final_spot), label='hedge p&l average',
# color='royalblue')
# ax[1].text(np.max(final_spot), hedge_mean, hedge_mean)
ax[1].legend()
ax[1].set_title('hedge p&l simulation')
plt.show()
if __name__ == '__main__':
call_option_replicating_simulation()코드는 전의 글 코드와 아주 비슷합니다. 바뀐 부분은
○ 코드 중간 부분 net_pl 변수를 long_spot_pl 로 정의하기. 즉, 기초자산의 매매에 따른 손익만 산출(식(2)의 우변!)
# net_pl = short_call_pl + long_spot_pl
net_pl = long_spot_pl # 이 부분만 바꾼다!
○ 콜옵션 만기페이오프 그래프에서 현재시점의 콜옵션 프리미엄을 뺀 값 (식(2)의 좌변!) 산출하기
spot_vec = np.linspace(50, 150, 100 + 1)
call_payoff = np.maximum(spot_vec - strike, 0)
call_payoff -= callval_series[0]
○ 기타 이 코드에서 쓸모없는 부분 주석처리
입니다. 결과를 볼까요?
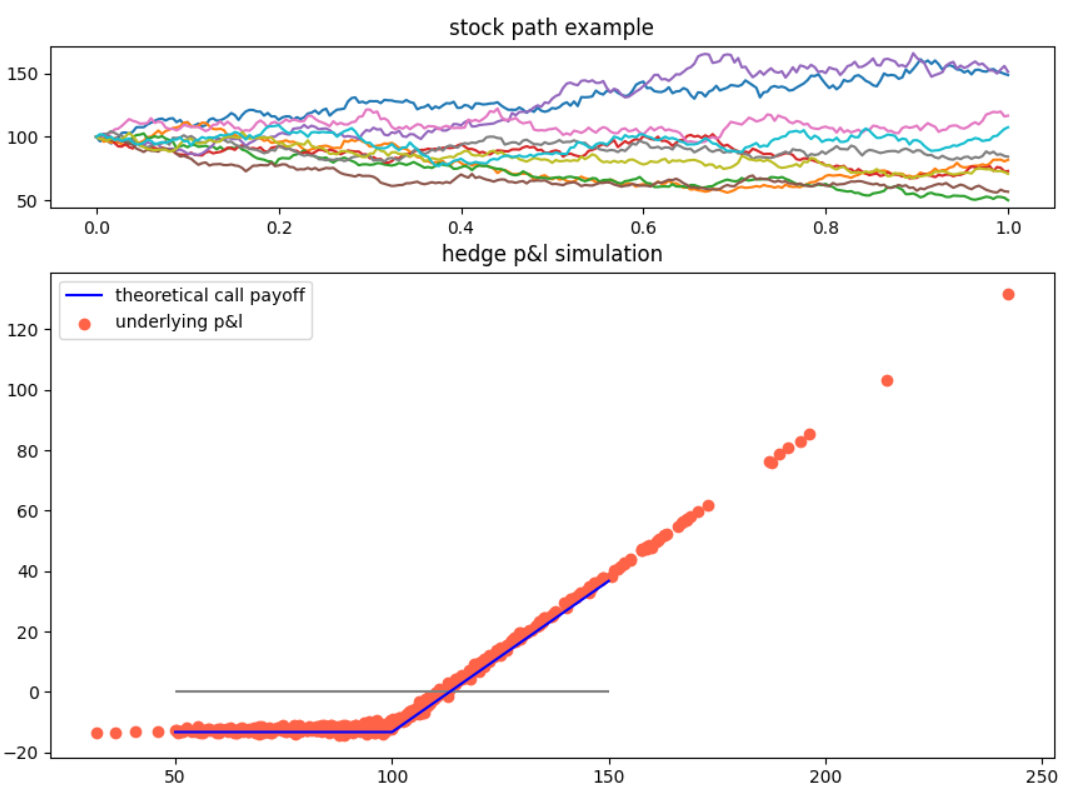
기초자산 매매 손익을 의미하는 빨간 점들을 보시죠. 콜옵션이 만기 페이오프스럽죠? 그런데 이게 0 보다 조금 아래로 내려가 있습니다.(회색 수평선이 0 선) 이 내려간 만큼이 바로 현재의 콜옵션 프리미엄입니다.
파란색 선은 콜옵션 만기페이오프에서 프리미엄을 뺀 이론적인 그래프인데 어떻나요. 빨간 점들 뭉치와 제법 일치합니다.
이렇게, 기초자산 주식을 어떤 규칙(델타)을 따라 샀다 팔았다 하며 쌓은 손익은 결국에는 콜옵션 페이오프를 만들어내게 됩니다.
즉,
콜옵션을 복제한다!
라는 거죠.
헤지(hedge)는 복제(replicating)와 같은 의미입니다.

더 알아볼 것은?
궁금증이 한 가지 정도 생깁니다. 전 글의 한 가지 의문은 해결했죠.
첫 번째는, 과연 행사가 근처에서 주가가 끝날 때, 헤지 성과가 좀 떨어지는 것으로 보이는데요. Brownian Bridge 방법을 사용하여 강제적으로 만기종가가 행사가에서 끝날 때를 가정해서 시뮬레이션해 볼 필요가 있을 것 같습니다.
두 번째는, 이처럼 콜옵션 매도포지션이 주가의 움직임으로 헤지가 되면,
주가의 움직임 만으로 콜옵션 가격을 복제(replicating)할 수 있지 않을까?
에 대한 것입니다.
기초자산을 샀다 팔았다 하면서, 콜옵션 보유의 효과를 누릴 수 있지 않을까?
라는 의문이죠.
다음 글을 통해 알아보도록 하겠습니다.
'금융공학' 카테고리의 다른 글
| 세타: 시간의 흐름이 콜옵션에 미치는 영향 (0) | 2023.05.19 |
|---|---|
| 콜옵션 가격 변동 헤지 시뮬레이션: 주가가 만기까지 횡보한다면.. (0) | 2023.05.12 |
| 콜옵션 가격 변동 헤지(hedge) 시뮬레이션 (0) | 2023.05.09 |
| 콜옵션 가격 변동 리스크를 없애보자! (0) | 2023.05.08 |
| 델타, 감마, 스피드! 콜옵션의 가격 변화를 쫓아가보자 #2 (0) | 2023.05.03 |




댓글