이 글은
2022.07.04 - [수학의 재미/행렬 이론] - 공분산과 공분산 행렬
공분산과 공분산 행렬
어떤 현상이나 타깃을 관찰하다 보면 여러 특징(features)들이 있습니다. 예를 들어 사람을 관찰할 경우 키, 몸무게, 나이 등등 학생 학습 성취도를 관찰할 경우: 국어 점수, 수학 점수 등 그런데 경
sine-qua-none.tistory.com
을 엑셀의 함수들을 사용하여 구해보는 글입니다.
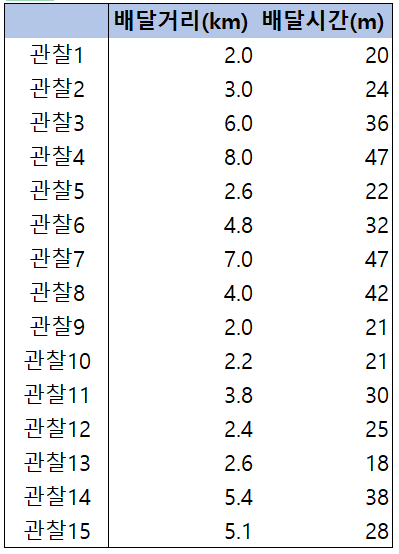
저번 글에서 봤던 데이터입니다. 다시 한번 살펴보면 공분산은 2가지 방법으로 구할 수 있다고 했습니다.
$p$개의 변수(features) $X_1, X_2, \cdots, X_p$ 가 있고 각각이 $n$개의 관찰 데이터 샘플을 가지고 있는 상황에서, 즉
$$
\pmatrix
{
\mid & \mid & & \mid \\
X_1 & X_2 & \cdots & X_p \\
\mid & \mid & & \mid
} =
\pmatrix
{
x_{11} & x_{12} & \cdots & x_{1p} \\
x_{21} & x_{22} & \cdots & x_{2p} \\
\vdots & \vdots &\ddots &\vdots \\
x_{n1} & x_{n2} & \cdots & x_{np} \\
}
$$
에서 공분산행렬 $\mathbf{C}$는 다음과 같이 구합니다. 각 $i\leq p$에 대해 $\mathbb{E}(X_i)=\mu_i$라 하면,
방법 1
$1\leq i , j \leq p$ 에 대해,
$$\mathbf{C}_{ij} = \mathbb{E}(X_i-\mu_i)(X_j-\mu_j) = \mathbb{E}(X_i X_j) - \mathbb{E}(X_i)\mathbb{E}(X_j)$$
방법 2.
$$ \mathbf{X} = \pmatrix { \mid & \mid & & \mid \\ X_1-\mu_1 & X_2-\mu_2 & \cdots & X_p-\mu_p \\ \mid & \mid & & \mid } $$
라 놓고
$$ \mathbf{C} = \frac{1}{n} \mathbf{X}^T \mathbf{X} $$
를 이용하여 구하기
하나하나 살펴보겠습니다.
방법 1. 공분산 행렬의 각 원소를 COVARIANCE 함수로 구하기
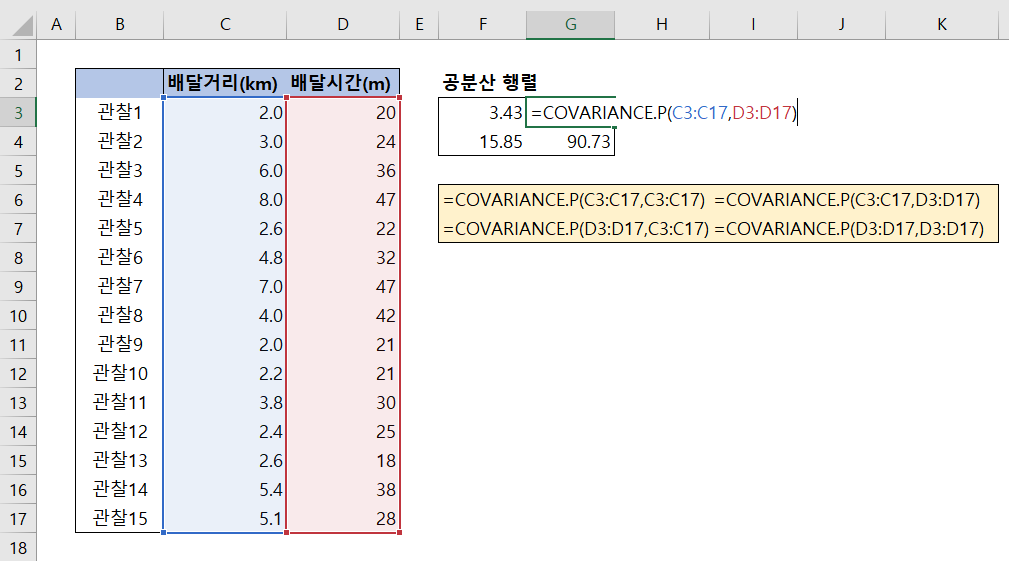
엑셀에 두 통계 변수의 공분산을 구하는 함수는
- COVARIANCE.P : 두 데이터 집단 사이의 모집단 공분산
- COVARIANCE.S : 두 데이터 집단 사이의 표본 집단 공분산
두 가지가 있습니다.
표본집단의 공분산은 여기서 다룬 STDEV처럼 불편 추정량을 구하는 것입니다. 수식으로 써보면 $n$개의 데이터로 이루어진 변수 $X=(x_i) $와 $Y=(y_i)$에 대해,
$$
\begin{align}
\mathbf{COVARIANCE.P} & = \frac 1n \sum_{i=1}^n (x_i-\mu_X) (y_i -\mu_Y) \\
\mathbf{COVARIANCE.S} & = \frac 1{n-1} \sum_{i=1}^n (x_i-\mu_X) (y_i -\mu_Y), \\
\end{align}
$$
이고 $\mu_X = \frac1n \sum x_i , \mu_Y = \frac1n \sum y_i$입니다.
직접 엑셀로 검증해 보겠습니다.
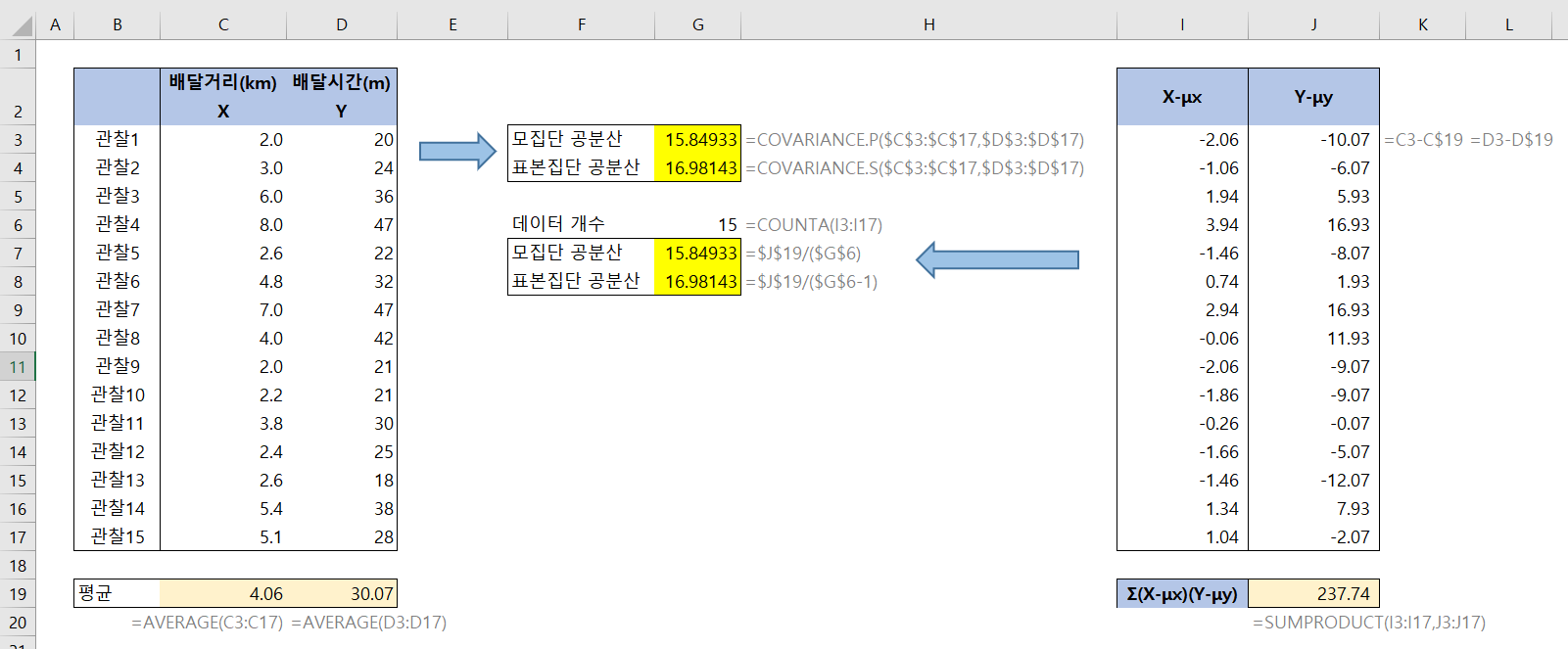
○ 셀 C19, D19에 X, Y의 평균을 구합니다. AVERAGE() 사용 → $\mu_X, \mu_Y$ 계산
○ I열 , J열에 C, D열에서 각각의 평균을 빼준 배열을 만듭니다.
○ 두 배열의 원소의 곱의 합, 즉 내적을 구합니다. SUMPRODUCT() 사용 → $\sum (x_i-\mu_X)(y_i -\mu_Y)$ 계산
○ 셀 G6에 데이터 개수를 구합니다. COUNTA() 사용
○ 셀 G7, G8에 모집단의 공분산, 표본집단의 공분산을 구합니다.
○ 셀 G3, G4와 비교합니다.
방법 2를 이용하기

○ 각 데이터에서 평균을 뺀 $X$라는 배열을 준비합니다. (F, G열)
○ RANGE(I3:J4) 영역에 빨간 네모 박스 친 수식을 걸어줍니다. 좀 더 분석해 보면
- TRANSPOSE(F3:G17) 로 $X^T$를 의미합니다.
- F3:G17 은 $X$를 의미합니다.
- MMULT는 두 배열의 곱입니다. 즉 $X_T X$를 의미합니다.
- COUNTA(F3:F17)은 데이터의 개수입니다.
- 주의할 점: 결과가 배열로 나와야 하므로 배열 수식을 걸어줘야 합니다. 배열 수식은
원하는 영역을 선택한 후, 수식을 입력하고 Ctrl + Shift + Enter를 치면 됩니다.
위 그림의 빨간 영역처럼 { } 괄호로 묶인 수식이 나오게 됩니다.
따라서 방법 1이나 방법 2나 모두 똑같은 결과를 얻습니다. 저번 글에서 처럼 python을 이용하면 쉬우나, 실무에서는 엑셀을 사용한 데이터 분석도 많이 하기 때문에 알아두면 유용할 것 같군요.
끝으로 분석에서 썼던 엑셀 함수 리스트입니다.
| AVERAGE | COVARIANCE.P | COVARIANCE.S | COUNTA |
| SUMPRODUCT | MMULT | TRANSPOSE |
'엑셀' 카테고리의 다른 글
| 트렌드 곡선 구하기 - 지수 (0) | 2022.05.16 |
|---|---|
| 트렌드 곡선 구하기 - 거듭제곱 (0) | 2022.05.15 |
| 트렌드 직선의 비밀(선형회귀) 엑셀실습 #2 (0) | 2022.05.13 |
| 트렌드 직선의 비밀(선형회귀) 엑셀실습 #1 (0) | 2022.05.13 |
| STDEV 함수 (0) | 2022.05.09 |




댓글