이 글은
2022.05.15 - [엑셀] - 트렌드 곡선 구하기 - 거듭제곱
트렌드 곡선 구하기 - 거듭제곱
이 글은 2022.05.13 - [엑셀] - 트렌드 직선의 비밀(선형회귀) 엑셀실습 #1 트렌드 직선의 비밀(선형회귀) 엑셀실습 #1 이 글은 2022.05.12 - [수학의 재미] - 트렌드 직선의 비밀(선형회귀) #3 트렌드 직선
sine-qua-none.tistory.com
에서 이어집니다. 저번 글에서는 거듭제곱 유형의 트렌드 곡선을 얻는 방법과 이론적인 배경을 알아 봤습니다.
오늘은 지수형입니다.
| 구분 | 수식 |
| 지수 | $y=ae^{bx}$ |
| 로그 | $y=a \ln(x) +b$ |
| 다항식 | $n$차 다항식 $y=a_nx^n + a_{n-1}x^{n-1}+\cdots+a_1x+a_0$ |
| 거듭제곱 | $y=ax^b$ |
2. 지수형 추세선
예제를 보겠습니다.
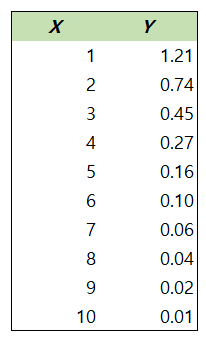
설명을 위한 데이터라, 좀 작위적인 느낌이 있어도 이해 바랍니다.
이 데이터를 분산차트로 그려보면 다음과 같습니다.
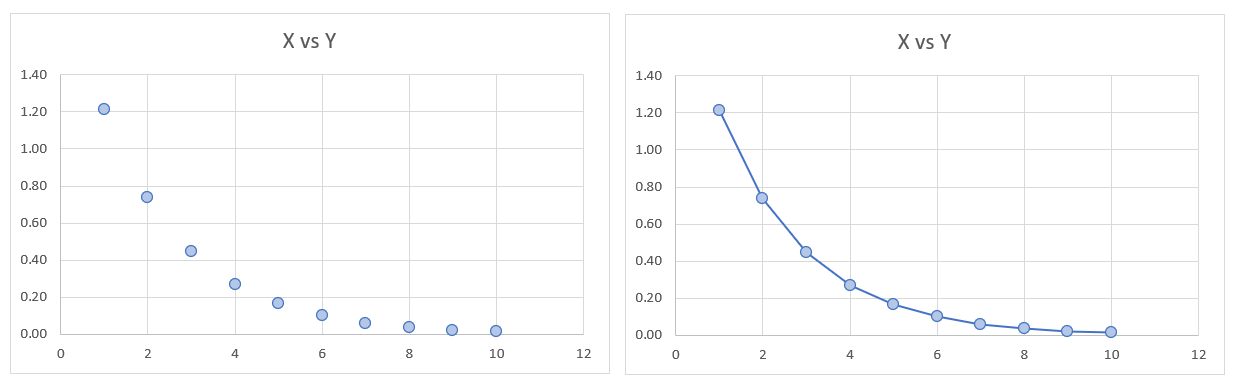
왼쪽은 분산차트이고, 오른쪽은 데이터들을 점선으로 이어 본 것입니다. 딱 보더라도 이 곡선형태의 데이터들을 직선으로 설명하는 것은 한계가 있어보입니다. 실제로 한번 그려볼까요?

$R^2$ 을 보면, 0.749 정도됩니다. 사실, 이정도면 통계 분석하에서는 높은 숫자로 간주가 되긴 합니다. 하지만 더욱 설명력 있는 선을 찾기 위해서 엑셀에서 제공하는 몇몇 추세선을 그려볼까요?
커브가 있는 곡선이니, 앞 글에서 살펴봤던 거듭제곱형도 후보가 될 수 있고, 로그형도 후보가 될 수 있고, 지수형도 후보가 될 수 있습니다.
우선 거듭제곱형과 로그형을 그려봅시다.
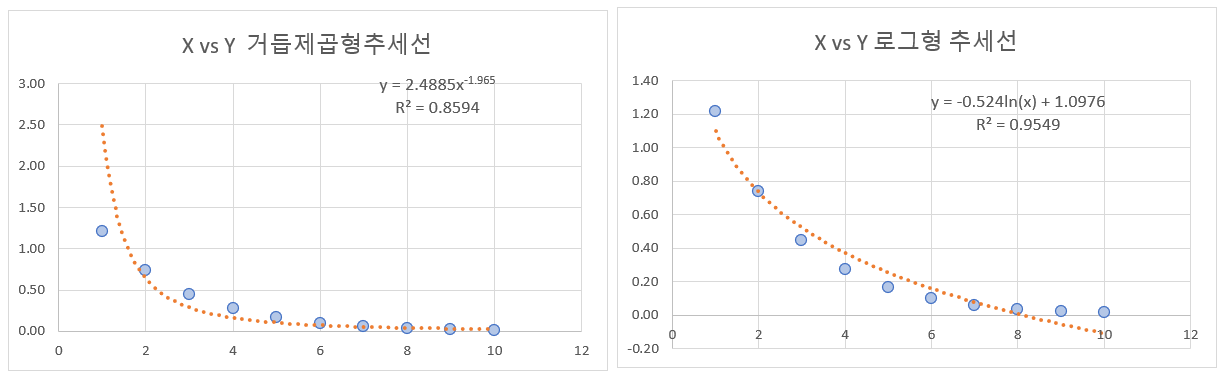
위 그림은 거듭제곱형과 로그형추세선을 각각 그려본 것인데요, $R^2$값이 각각 0.86, 0.95 입니다.
직선으로 유추했을때보다 많이 높아졌죠? 지수형 추세선도 한번 그려봅시다.

어떤가요? 아예 $R^2 =1$ 이 나올 정도로 완벽하게 설명이 되는 모습을 볼 수 있습니다.(사실 데이터를 이렇게 작위적으로 만든 것입니다.)
선형, 거듭제곱, 로그 추세선을 쓰면서 $R^2$이 1로 가까이는 갔지만, 뭔가 아쉬웠던 것이 사실입니다. 하지만 지수형 추세선을 써서 데이터를 완벽 분석했습니다. 이제 남은 것은
$$ y=2e^{-0.5x}, R^2=1 $$
이라는 수학적 결과입니다. 이것은 어떻게 나온 것일까요?
앞서 지수형 추세선의 일반적인 형태는
$$ y= ae^{bx}$$
라고 했습니다. 양변에 자연로그를 취해보면
$$ \ln y = b x + \ln a $$
입니다. 감이 좀 오는가요? 애시당초 주어진 데이터 $(x,y)$를 $( x, \ln y)$ 로 바꾸어 선형직선을 구한다면
$b$ 가 기울기(slope), $\ln a$ 가 $y$절편(intercept)
인 선형직선이 되는 것입니다.
우리는 앞선 예제에서 선형직선의 기울기, $y$절편, 그리고 $R^2$ 값을 구하는 엑셀 함수를 다뤘습니다. 이를 이용해 보죠.
우선 데이터를 $(x,y)$에서 $(x, \ln y)$로 바꿉니다.
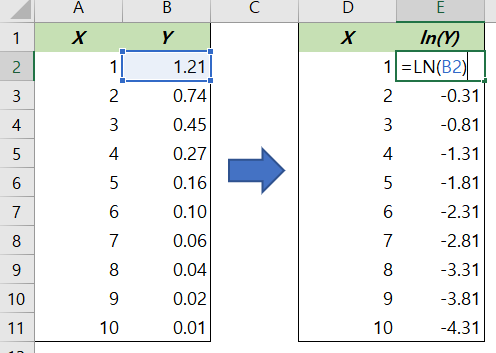
엑셀에서 LN() 함수를 쓰면 자연로그 값을 출력해줍니다. 위처럼 데이터에 자연로그를 모두 씌웁니다.
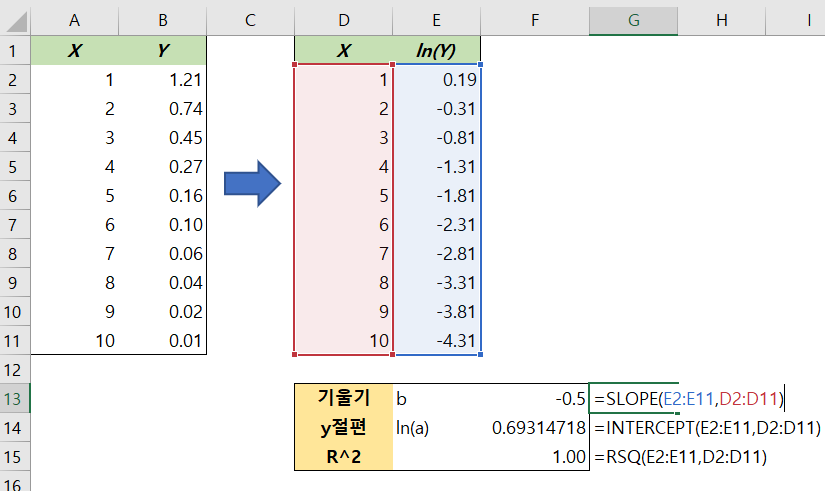
SLOPE, INTERCEPT, RSQ 함수를 써서 $(x, \ln y$)의 추세직선이 만드는 기울기, $y$절편 그리고 $R^2$값을 얻어 냅니다.
따라서
$$b=-0.5, \ln(a) = -0.69314718$$
을 얻었습니다. $a$를 구하기 위해서는
$$a= \exp(\ln(a)) = exp(-0.69314718) =2$$
이렇게 얻습니다.
따라서 지수형 추세선은
$$y= 2\exp(-0.5 x) $$
가 나오게 되는 것입니다.
다음 글에서는 로그형 추세선 설계하는 것에 대해 다뤄 보겠습니다.
'엑셀' 카테고리의 다른 글
| 공분산 행렬을 엑셀로 구하기 (0) | 2022.07.05 |
|---|---|
| 트렌드 곡선 구하기 - 거듭제곱 (0) | 2022.05.15 |
| 트렌드 직선의 비밀(선형회귀) 엑셀실습 #2 (0) | 2022.05.13 |
| 트렌드 직선의 비밀(선형회귀) 엑셀실습 #1 (0) | 2022.05.13 |
| STDEV 함수 (0) | 2022.05.09 |




댓글