이 글은
2022.05.13 - [엑셀] - 트렌드 직선의 비밀(선형회귀) 엑셀실습 #1
트렌드 직선의 비밀(선형회귀) 엑셀실습 #1
이 글은 2022.05.12 - [수학의 재미] - 트렌드 직선의 비밀(선형회귀) #3 트렌드 직선의 비밀(선형회귀) #3 이 글은 2022.05.11 - [수학의 재미] - 트렌드 직선의 비밀(선형회귀) #2 트렌드 직선의 비밀(선형
sine-qua-none.tistory.com
과 관련이 있습니다. 지금까지는 트렌드 직선에 대해서 알아봤었는데요. 데이터가 모두 직선으로 설명되는 것은 아닙니다. 일반적으로 다양한 곡선으로 데이터를 설명할 수 있습니다.
엑셀에서는 추세 곡선 여러 종류를 제공해 줍니다.
엑셀 추세선 추가 (이 과정은 위의 플러그 인에서 확인 가능) 를 해 보면 다음과 같은 추세선 유형들이 뜹니다.

지금까지는 선형에 대해서 알아보았다면, 이제 지수, 로그 등등 다양한 추세선 그리는 것을 알아보겠습니다.
각각에 대한 수식은 다음과 같습니다.
| 구분 | 수식 |
| 지수 | $y=ae^{bx}$ |
| 로그 | $y=a \ln(x) +b$ |
| 다항식 | $n$차 다항식 $y=a_nx^n + a_{n-1}x^{n-1}+\cdots+a_1x+a_0$ |
| 거듭제곱 | $y=ax^b$ |
거듭제곱 추세선 부터 살펴보겠습니다.
1. 거듭제곱 추세선
예제를 보겠습니다.

설명을 위한 데이터이니 데이터가 요상하게 생겼어도 이해바랍니다.
이 데이터를 분산차트로 그려보면 다음과 같습니다.

왼쪽은 분산차트이고, 오른쪽은 데이터들을 점선으로 이어 본 것입니다.
한눈에 딱 봐도 이 데이터 들이 그리는 모양새는 직선으로 설명이 안 되는 것 같습니다. 실제로 추세직선을 그려서 그래프의 모형과 $R^2$를 살펴보면

이 됩니다. $R^2$는 0.9056으로 아주 높아 굳이 선형으로 분석하려면 이방법을 써도 됩니다.
하지만 데이터가 이루는 개형은 우리가 중학교때부터 많이 보던 함수랑 비슷하게 생겨 있습니다. 바로
$$y=\sqrt{x}$$
그래프이죠. 그래서 생각을 해보는 것입니다.
아, 데이터의 모양이 위로 볼록한 것이 제곱근 형태이므로 이 데이터는 직선이 아니라 제곱근 비스무레한 곡선으로 더 설명이 잘 되지 않을까? 그렇다면 엑셀의 거듭제곱 형태의 추세곡선으로 유추해보자!

어떻습니까? 다음의 두 가지 개선된 효과를 얻을 수 있습니다.
- 그래프의 개형이 비슷하게 나온다.
- $R^2$값이 드라마틱하게 개선되었다.
여러 모로, 선형 추세선으로 근사한것보다 훨씬 나는 결과를 얻게 되는 것입니다.
그럼 과연 $R^2$ 값과 $y=1.8538x^{0.521}$이라는 식은 어떻게 나온 것일까요? 곡선에 대해서는 알아본적이 없는데요. 그 원리는 다음과 같습니다.
앞서 거듭제곱 추세선의 일반적인 형태는
$$ y= ax^b$$
라고 했습니다. 양변에 자연로그를 취해보면
$$ \ln y = b \ln x + \ln a $$
입니다. 감이 좀 오는가요? 애시당초 주어진 데이터 $(x,y)$를 $(\ln x, \ln y)$ 로 바꾸어 선형직선을 구한다면
$b$ 가 기울기, $\ln a$ 가 $y$절편
인 선형직선이 되는 것입니다.
우리는 앞선 예제에서 선형직선의 기울기, $y$절편, 그리고 $R^2$ 값을 구하는 엑셀 함수를 다뤘습니다. 이를 이용해 보죠.
우선 데이터를 $(x,y)$에서 $(\ln x, \ln y)$로 바꿉니다.
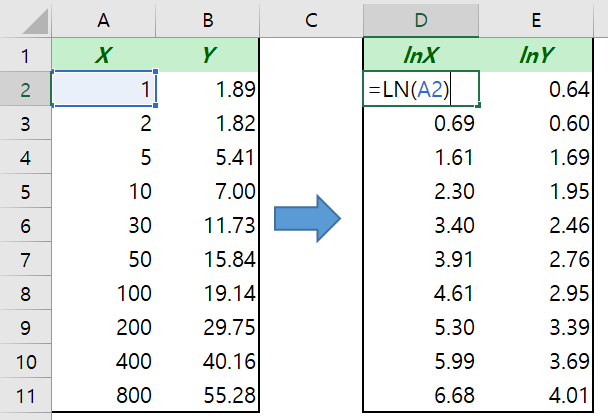
엑셀에서 LN() 함수를 쓰면 자연로그 값을 출력해줍니다. 위처럼 데이터에 자연로그를 모두 씌웁니다.
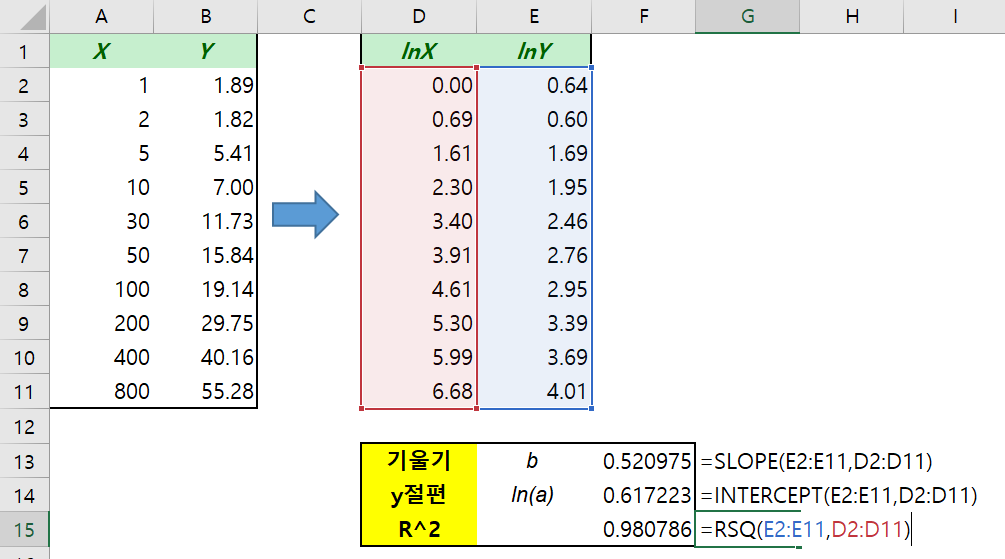
SLOPE, INTERCEPT, RSQ 함수를 써서 $(\ln x, \ln y$)의 추세직선이 만드는 기울기, $y$절편 그리고 $R^2$값을 얻어 냅니다.
이제 마무리를 지을까요? 위에서 구한 기울기 $b$와 $y$절편 $\ln a$에서 다시 $a,b$를 얻습니다.

이것이 바로 $R^2$ 값과 $y=1.8538x^{0.521}$이라는 식이 나오게 된 원리입니다.
다음 글에서는 지수형 추세선 설계하는 것에 대해 다뤄 보겠습니다.
'엑셀' 카테고리의 다른 글
| 공분산 행렬을 엑셀로 구하기 (0) | 2022.07.05 |
|---|---|
| 트렌드 곡선 구하기 - 지수 (0) | 2022.05.16 |
| 트렌드 직선의 비밀(선형회귀) 엑셀실습 #2 (0) | 2022.05.13 |
| 트렌드 직선의 비밀(선형회귀) 엑셀실습 #1 (0) | 2022.05.13 |
| STDEV 함수 (0) | 2022.05.09 |




댓글