지난 글에서 길 따라 걷는 1차원적인 random walk에 대해서 알아봤습니다.
2022.06.25 - [수학의 재미/확률분포] - 술 먹고 걷기(Random Walk) #1: 길 따라 걷기
술먹고 걷기(Random Walk) #1: 길따라 걷기
지난 글에서 마팅게일을 다루면서, random walk라는 프로세스가 마팅게일이 된다는 이야기를 했었죠. 2022.06.23 - [수학의 재미/확률분포] - 조건부 기댓값과 마팅게일(martingale) #1 조건부 기댓값과 마
sine-qua-none.tistory.com
이번 글에서는 술취한 사람이 동서남북 4방향으로 걸어 다닌다고 합시다. 이게 더 현실적이겠죠.

동서를 나타내는 확률변수를 XX, 남북을 나타내는 확률변수를 YY라고 합시다. 그리고 1차원 random walk 때처럼 XX,YY를 각각 1, -1을 가지는 확률변수라 해 보죠.
| (X,Y)(X,Y) | (1,0) | (-1,0) | (0,1) | (0,-1) |
| 확률 | 1414 | 1414 | 1414 | 1414 |
| 방향 | 동 | 서 | 북 | 남 |
그리고 (X1,Y1),(X2,Y2),cdots(X1,Y1),(X2,Y2),cdots를 (X,Y)(X,Y)의 i.i.d 라고 합시다. (X,Y)(X,Y)의 평균은
E(X,Y)=14(1,1)+14(1,−1)+14(−1,1)+14(−1,−1)=(0,0)
즉, 원점이 나오게 됩니다.
이제
N∑i=1(Xi,Yi)
를 하면 바로 이것이 2차원 random walk 가 됩니다.
자, 이제 이 친구가 어디로 가나 봅시다. 1차원 random walk 분석과 같은 방법으로 code를 작성합니다.
import math
import numpy as np
import matplotlib.pyplot as plt
def random_walk():
nSimulation = 500
nSteps = 1000
x_finish =[]
y_finish=[]
for _ in range(nSimulation):
x = []
y = []
x0, y0 = 0, 0
x.append(x0)
y.append(y0)
a, b = x0, y0
for _ in range(nSteps):
rd = np.random.randint(1, 5)
if rd == 1:
a += 1
b += 0
elif rd == 2:
a += -1
b += 0
elif rd == 3:
a += 0
b += 1
else:
a += 0
b += -1
x.append(a)
y.append(b)
x_finish.append(x[-1])
y_finish.append(y[-1])
plt.subplot(121)
plt.plot(x, y, color='c', marker='o')
plt.scatter(x[0],y[0], color='b', s=100, marker='s')
plt.text(x[0],y[0],'start')
plt.scatter(x[-1],y[-1], color='r', s=100, marker='s')
plt.text(x[-1],y[-1],'finish at ({},{})'.format(x[-1],y[-1]))
plt.title('Example of random walk')
plt.subplot(122)
plt.plot(x_finish, y_finish, color='m', marker='o', linestyle='')
plt.scatter(x_finish[-1], y_finish[-1], color='r', s=100, marker='s')
plt.text(x_finish[-1], y_finish[-1], 'location:({},{})'.format(x_finish[-1],y_finish[-1]))
plt.scatter(0, 0, color='b', s=100, marker='s')
plt.text(0, 0, 'start')
plt.title('{} times random walk result'.format(nSimulation))
plt.show()
print(np.mean(x_finish))
print(np.mean(y_finish))
if __name__ == '__main__':
random_walk()
전체적인 것은 1차원 random walk와 비슷합니다. 다만, 동서남북으로 갈 수 있는 세팅을 해 줘야겠죠.
for _ in range(nSteps):
rd = np.random.randint(1, 5)
if rd == 1:
a += 1
b += 0
elif rd == 2:
a += -1
b += 0
elif rd == 3:
a += 0
b += 1
else:
a += 0
b += -1
x.append(a)
y.append(b)바로 이 부분입니다.
○ np.random.randint(1,5)를 써서 1,2,3,4 중 하나를 선택하는 난수를 발생시킵니다.
○ 각각의 방향에 따라 좌표를 1,-1 씩 더해주는 연산을 합니다.
○ x방향(동/서 방향)으로 random walk, y방향(남/북)으로 random walk를 만들어 줍니다.
x_finish.append(x[-1])
y_finish.append(y[-1])○ nSimulation 번 시뮬레이션을 통해 술 취한 양반의 최종 목적지인 x[-1], y[-1] 을 저장하는 리스트를 만듭니다.
plt.subplot(121)
plt.plot(x, y, color='c', marker='o')
plt.scatter(x[0],y[0], color='b', s=100, marker='s')
plt.text(x[0],y[0],'start')
plt.scatter(x[-1],y[-1], color='r', s=100, marker='s')
plt.text(x[-1],y[-1],'finish at ({},{})'.format(x[-1],y[-1]))
plt.title('Example of random walk')○ 차트 두 개를 그릴 것입니다. subplot을 이용하여 1*2 그림 배열을 만들고 첫번째 영역을 선택합니다.
○ 현재 x, y 에는 마지막 시뮬레이션의 random walk가 저장되어 있을건데, 그것을 그려줍니다.
plt.subplot(122)
plt.plot(x_finish, y_finish, color='m', marker='o', linestyle='')
plt.scatter(x_finish[-1], y_finish[-1], color='r', s=100, marker='s')
plt.text(x_finish[-1], y_finish[-1], 'location:({},{})'.format(x_finish[-1],y_finish[-1]))
plt.scatter(0, 0, color='b', s=100, marker='s')
plt.text(0, 0, 'start')
plt.title('{} times random walk result'.format(nSimulation))
plt.show()○ 술취한 양반 500명의 최종 도착지를 plotting 해 본 것입니다.
○ 마지막 양반의 도착지점은 왼쪽 그림과 비교해 볼 수 있도록 특별히 location을 출력해 줍니다.
이제 결과를 볼까요?
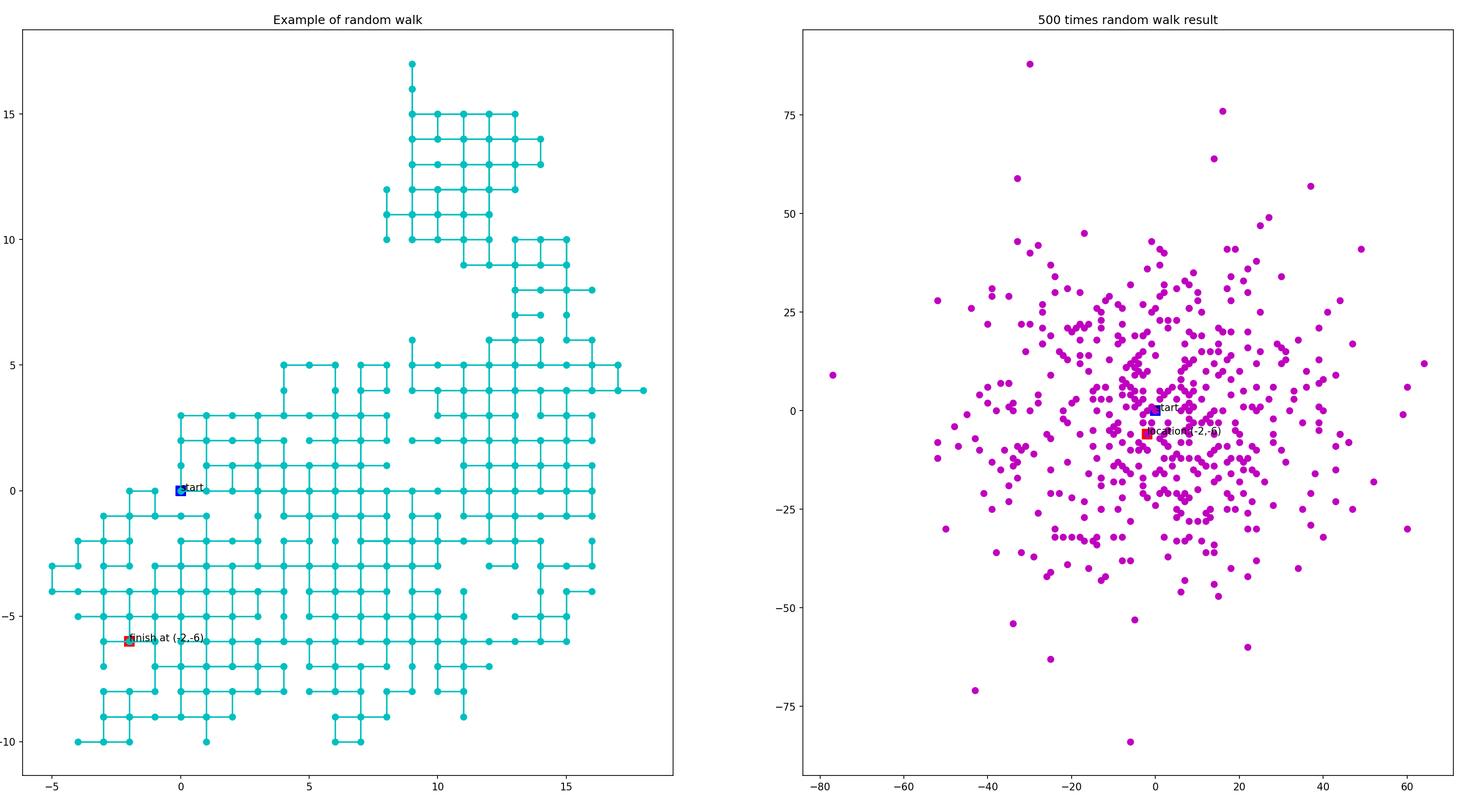
0.706
-0.894
Process finished with exit code 0오른쪽 차트의 500명의 평균 좌표를 출력해 보니 위와 같았습니다. 거의 영점이었죠.
술 취한 양반들이 동서남북이 아닌 북동, 북서, 남동, 남서로 싸돌아다니면 그림이 조금 더 이뻐집니다. 위의 차트 중 방향 정해주는 부분만 바꾸면 됩니다.

for _ in range(nSteps):
rd = np.random.randint(1, 5)
rr.append(rd)
if rd == 1:
a += 1
b += 1
elif rd == 2:
a += -1
b += 1
elif rd == 3:
a += 1
b += -1
else:
a += -1
b += -1이렇게죠. 결과를 보시면
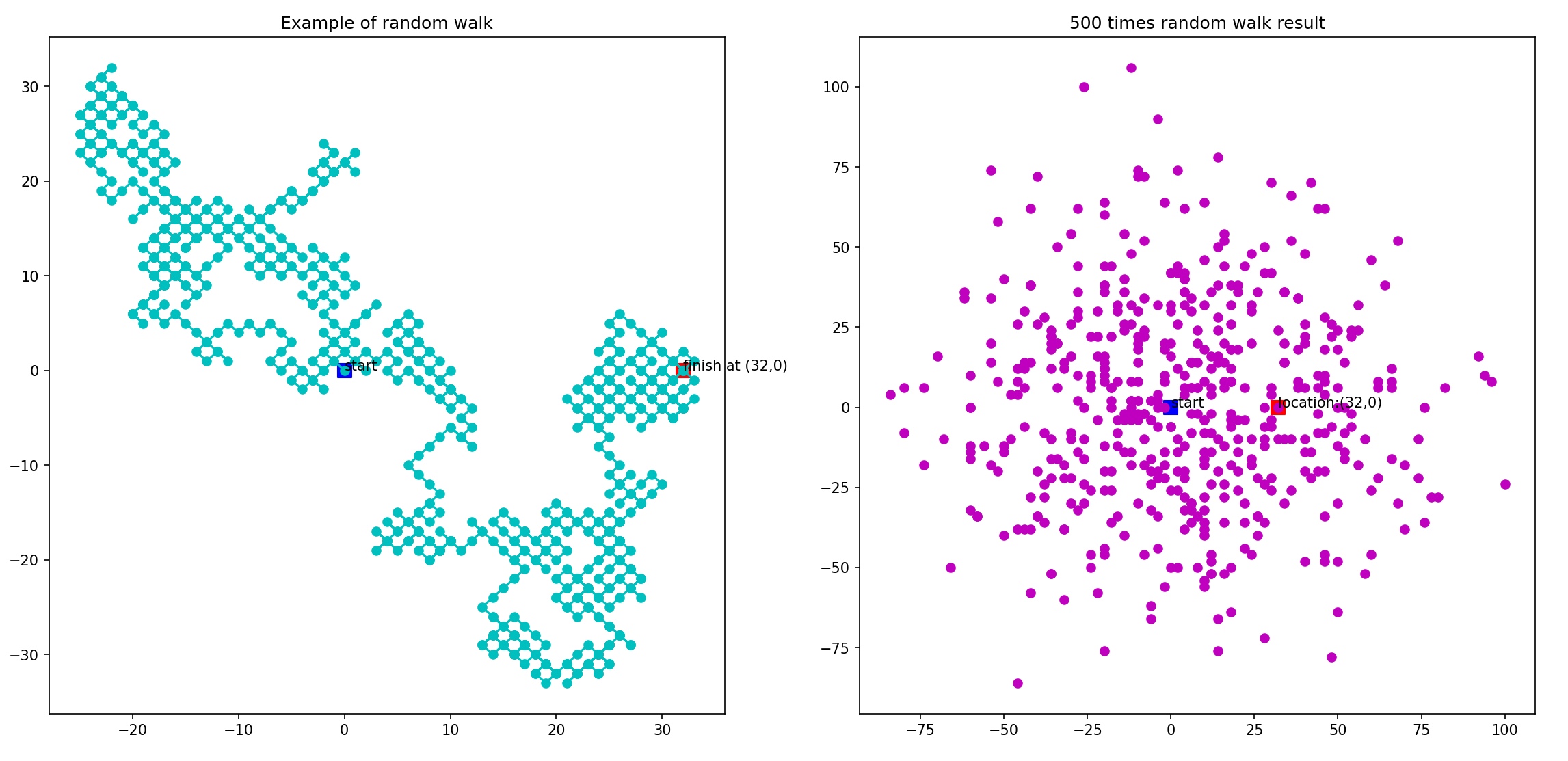
radom walk는 2차원에서 마무리 짓겠습니다. 술취한 양반들은 피곤해서 위아래로 움직이는 건 못하거든요. 이걸 동적인 차트로 움직이게끔 그려보는 것(여기를 참고해 보세요)도 재미있겠네요.
'수학의 재미 > 확률분포' 카테고리의 다른 글
| 상관관계가 있는 두개의 표준정규분포 난수 구하기 (0) | 2022.09.16 |
|---|---|
| 확률측도를 바꿉시다: Girsanov Theorem (1) | 2022.06.28 |
| 술먹고 걷기(Random Walk) #1: 길따라 걷기 (0) | 2022.06.25 |
| 마팅게일과 Ito Lemma (drift term이 없다고?) (0) | 2022.06.24 |
| 조건부 기댓값과 마팅게일(martingale) #2 (0) | 2022.06.24 |



댓글