이번 글은
2022.06.08 - [수학의 재미/확률분포] - 균등난수(uniform random number) 만들어보자 #1
균등난수(uniform random number) 만들어보자 #1
이번 글에서는 확률분포 중 가장 기본이 되는 연속 균등 확률분포(uniform distribution)와 균등 분포(uniform random number) 난수 생성에 대해서 이야기해보겠습니다. 실수 구간 [0,1]에서 정의된 연속 균
sine-qua-none.tistory.com
에서 이어집니다. 저번 글에서는 Von Neumann이라는 초천재 수학자가 균등 난수를 얻어내기 위해 썼던 알고리즘과 그 한계점에 대해서 알아봤습니다. 이 개념으로부터 균등 난수를 생성하는 알고리즘이 발전하기 시작했는데요, 이른바 LCG(Linear Congruential Generator)라는 알고리즘입니다. 전개될 내용은 이 사이트의 내용을 참고하여 정리한 것입니다.
개념은 이렇습니다.
- 난수를 생성하기 좋은 (아주)큰 자연수 M을 하나 고른다.
- 초기값이 될 자연수 m0을 하나 선택한다(m0<M.)
- m_{i+1} \equiv am_i + c \mod M ~,~ i\geq 0 인 점화식을 이용하여 \{m_i\}들을 생성한다.
- \frac{m_i}M을 하여 0과 1 사이의 난수를 만든다.
3번에서 \equiv 기호란, am_i +c를 M으로 나누어 나머지를 구하고 그것을 m_{i+1}이라 하자는 합동식입니다.
이왕 만들 거, 3번식으로 \{m_i\}들을 생성했을 때, 주기를 타면 안 되겠죠. 어차피 M으로 나눈 나머지 들이라 \{m_i\}들은 최대 M개가 나올 수밖에 없습니다. 하지만 반복 주기가 줄어들면 계산의 효용성이 떨어질 것입니다.

수학자들이 득달처럼 달려들어 위 알고리즘의 (a,c,M)의 관계를 정립했습니다. 아래의 조건을 만족하게끔 a,c,M을 잘 선택하면 주기가 M으로 아주 길어진다는 것을요.
- c는 M과 서로 소(relatively prime)이다.
- M의 임의의 소인수 g에 대해서, a\equiv 1 \mod g 이다.
- M이 4의 배수면, a\equiv 1 \mod 4 이다.
자세한 증명은 과감히 스킵하고 어쨌든 우리는 이 조건을 만족하는 a,c,M을 잘 선택하면 됩니다.
한 가지 더, 컴퓨터는 M=2^b 형태의 수를 좋아한다고 합니다. 이유는 컴퓨터는 0,1로 이루어진 이진 연산을 하기 때문인데요, 예를 들어, 10진법을 쓰는 우리들이 123456이라는 숫자를 1000으로 나눈 나머지를 뒤의 세 수(456)만 떼서 바로 얻어낼 수 있듯이, 컴퓨터는 2^b형태로 나누는 행위를 편안하게 느낍니다.
또 한다 하는 사람들이 득달같이 달려듭니다. 좋은 a,c,M 을 찾기 위해서요.

그래서 찾은 것이 대표적으로 아래와 같답니다.
| M | a | c |
| 2^{35} | 129 | 1 |
| 2^{32} | 69069 | 1 |
| 2^{32} | 1812433253 | 1 |
왠지 3번째 triple이 숫자도 복잡해 보이는 게, 난수 생성이 잘 될 거 같지만 실제로 두 번째 것이 훨씬 많이 사용된다 합니다. 32bit의 컴퓨터 환경에서 2^{32}를 핸들링 가능하고, 또한 69069는 기억할만하다는 것이 이유가 아닐까 합니다.
| M | a | c |
| 2^{32} | 69069 | 1 |
이 조합이 어떤 강점이 있는지, 다른 조합과 비교해 보겠습니다. 다른 한 조합은
a=25, c= 1, M=2^8인 경우입니다. 이 조합은 m_i의 주기가 기껏해야 2^8 = 256인 경우입니다. 날코딩을 보실까요?
import math
import numpy as np
import matplotlib.pyplot as plt
def lcm_generator():
m0=1
nSimulation = 1000
# a, c, M = 25, 1, 2 ** 8 일 때 uniform random number 생성
a, c, M = 25, 1, 2 ** 8
res =[]
res.append(m0/M)
for i in range(nSimulation):
m1 = (a*m0+c) % M
res.append(m1/M)
m0 =m1
x1 = res[0:nSimulation-1]
y1 = res[1:nSimulation]
# a,c,M = 69069, 1, 2**32 일 때 uniform random number 생성
a,c,M = 69069, 1, 2**32
res = []
res.append(m0 / M)
for i in range(nSimulation):
m1 = (a * m0 + c) % M
res.append(m1 / M)
m0 = m1
x2 = res[0:nSimulation - 1]
y2 = res[1:nSimulation]
plt.subplot(1,2,1)
plt.scatter(x1,y1, marker= '.', color='r')
plt.title('a=25, c=1, M=$2^8$')
plt.xlabel('$m_i$')
plt.ylabel('$m_{i+1}$')
plt.subplot(1, 2, 2)
plt.scatter(x2, y2, marker ='.', color='b')
plt.title('a=69069, c=1, M=$2^32$')
plt.xlabel('$m_i$')
plt.ylabel('$m_{i+1}$')
plt.show()
if __name__ == '__main__':
lcm_generator()실행을 하면 아래와 같은 차트가 뜹니다.

위 코드는 x축에 m_i, y축에 m_{i+1}을 scattering 한 것입니다. 뭔가 왼쪽은 정갈하고 오른쪽은 왼쪽보다는 좀 어지럽죠?
왼쪽 꺼는 m_i 사이에 상관관계가 존재한다는 것입니다. 반면에 오른쪽의 경우는 그 상관관계가 덜한 것 같습니다. 사람 눈에는 무작위로 찍혀 있어 보이지만, 이 난수를 만드는 알고리즘 자체가 선형이라 아무래도 직선 형태가 나올 가능성이 높지요.
George Marsaglia라는 저명한 수학자가 이미 암울한 증명을 했다고 합니다. 선형 합동식으로는 이 상관관계를 해결할 수 없다고.. 이런저런 단점을 극복하기 위해 난수 발생에 대한 수학자 및 컴퓨터 과학자들의 노력은 계속됩니다.
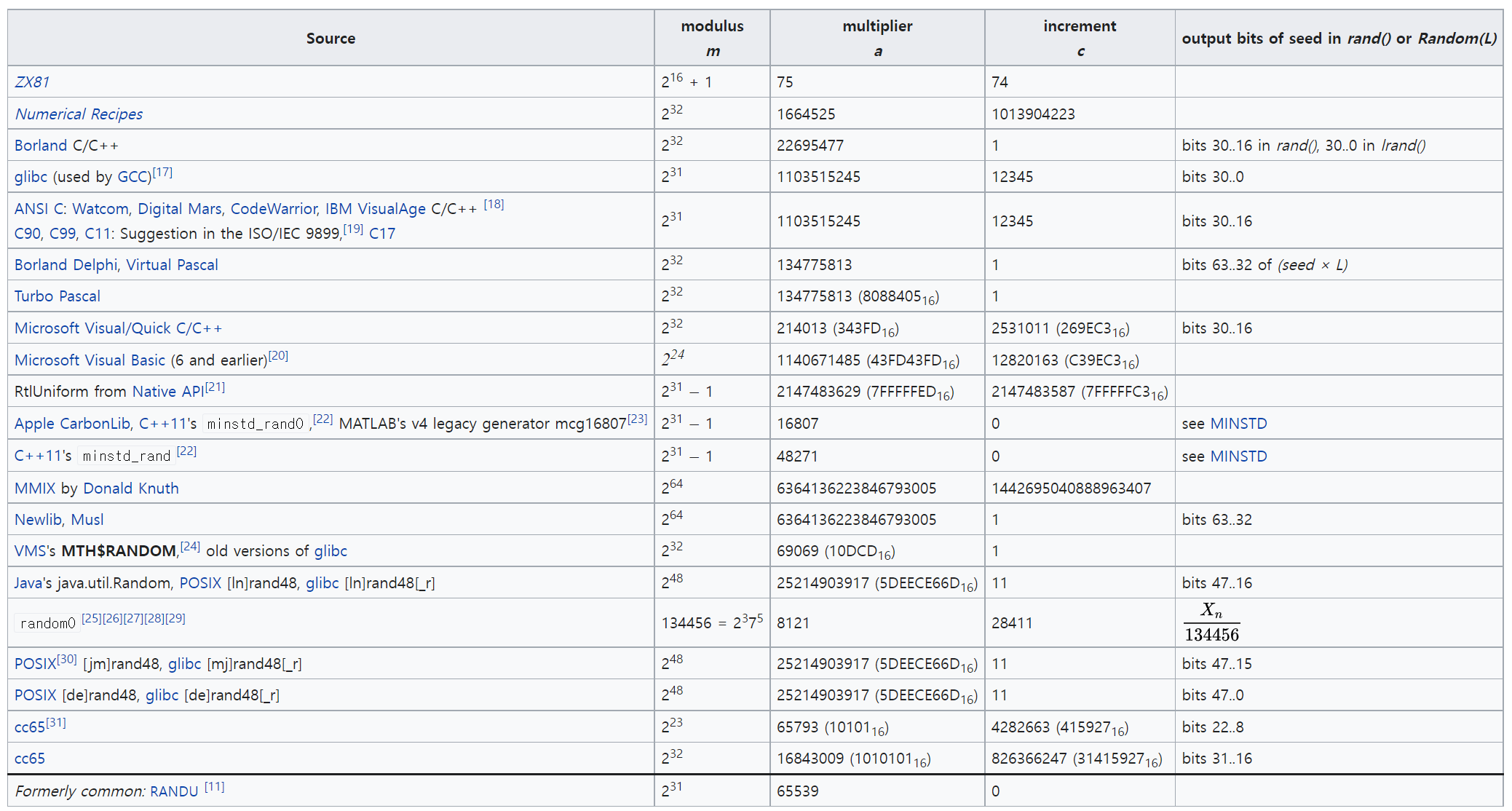
마지막으로 위키피디아 LCG 문서에 소개되어 있는 (a,c,M) 조합을 소개합니다. 위에서 알아본 경우(a=69069 조합)도 목록에 포함되어 있네요.
'수학의 재미 > 확률분포' 카테고리의 다른 글
| 정균분포 난수를 만들어 주세요 #1 : 중심극한정리 이용 (0) | 2022.06.13 |
|---|---|
| 중심극한정리: 평범한 것들은 정규분포이다. (0) | 2022.06.11 |
| 균등난수(uniform random number) 만들어보자 #3 : Halton Sequence (0) | 2022.06.10 |
| 균등난수(uniform random number) 만들어보자 #1 (0) | 2022.06.08 |
| Irwin-Hall Distribution (0) | 2022.05.25 |



댓글