이번 글은
2022.06.10 - [수학의 재미/확률분포] - 균등난수(uniform random number) 만들어보자 #2 : LCG
균등난수(uniform random number) 만들어보자 #2 : LCG
이번 글은 2022.06.08 - [수학의 재미/확률분포] - 균등난수(uniform random number) 만들어보자 #1 균등난수(uniform random number) 만들어보자 #1 이번 글에서는 확률분포 중 가장 기본이 되는 연속 균등 확률..
sine-qua-none.tistory.com
에서 이어집니다. 저번 글에서는 선형합동생성기라는 식을 사용하여 [0,1]사이의 균등 분포를 따르는 난수를 발생시켜 보았습니다. 하지만, 생성된 숫자들끼리 상관관계를 보이고, 이걸 원천적으로 없애기가 불가능하다는 얘기까지 했었죠. 그래서 신박한 방법으로 난수들을 만들어 내기 시작했는데요, 우선 Halton Sequence라는 것을 보도록 하겠습니다.
자연수 b≥2를 선택합니다. 자연수 N 에 대해서,
1. N을 b진법으로 표기합니다. 즉,
n=a0(n)+a1(n)b+a2(n)b2+⋯+ak(n)bk=k∑j=0aj(n)bj , 0≤aj(n)<b ∀j=0,1,⋯,k
예) b=2 라 하고, N=23 이라 하면, N=10111(2) 이므로
a0=1,a1=1,a2=1,a3=0,a4=1 이 상황입니다(k=4.)
2. 1에서 구한 ai들을 다음처럼 재구성하고 이 값을 ϕb(N)이라 씁니다.
ϕb(N)=(0.a0a1⋯ak)(b)=k∑j=0aj(n)b−j−1
예) ϕ2(23)=a0⋅12+a1122+a2123+a3124+a4125이므로 ϕ2(23)=2932=0.90625 입니다.
엑셀 사용자 정의 함수를 VBA로 코딩하여 결과를 살펴보겠습니다. VBA code는 아래와 같습니다.
Function HaltonSequence(base As Integer, num As Long) As Double
Dim tempValue As Double
Dim iBase As Double
Dim i As Long
Dim num0 As Long
Dim num1 As Long
num0 = num
tempValue = 0
iBase = 1 / base
Do While num0 > 0
num1 = Int(num0 / base)
i = num0 - num1 * base
tempValue = tempValue + iBase * i
iBase = iBase / base
num0 = num1
Loop
HaltonSequence = tempValue
End Function이 사용자정의 함수를 사용하여 엑셀에 데이터를 산출합니다.



이렇게 500개 행의 데이터가 생기도록 Drag 하여 데이터를 채워봅니다.

- B열과 C열 (Halton Sequence 끼리)
- D열과 E열 (컴퓨터 제공 난수끼리)
분산 차트를 그리면 아래와 같습니다.

어떤 그림이 쫌 더 고르게 분포되어 보이나요? 좌측 그래프가 좀 더 고르게 분포되어 보입니다. 하지만 Halton Sequence도 Base를 어떻게 잡느냐에 따라 심한 경향성을 보일 때가 있습니다. 아래 그림을 보시죠.

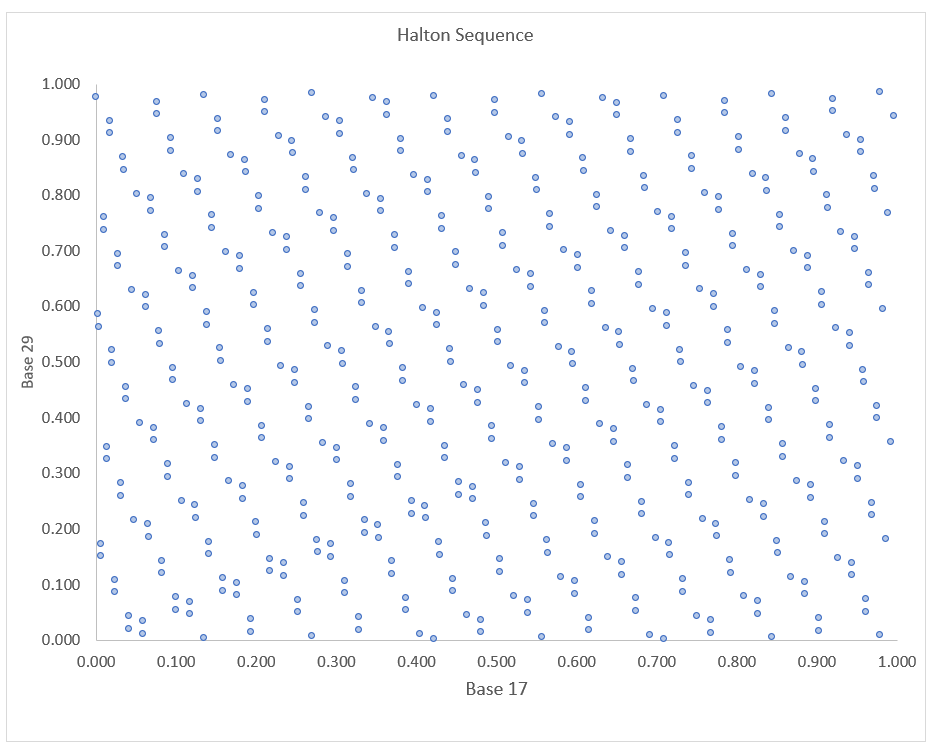
python으로도 작성해 보았습니다.
import math
import numpy as np
import matplotlib.pyplot as plt
def HaltonSequence(base, num):
num0 = num
tempValue = 0
iBase = 1/base
while num0 >0:
num1 = num0//base
i= num0 -num1*base
tempValue += i*iBase
iBase /= base
num0 = num1
return tempValue
def HalonSequence_test():
base1, base2 = 2, 3
nSimulation = 2000
x=[]
y=[]
for i in range(nSimulation):
x.append(HaltonSequence(base1, i+1))
y.append(HaltonSequence(base2, i+1))
plt.scatter(x,y, s=5)
plt.xlabel('Halton(base: {})'.format(base1))
plt.ylabel('Halton(base: {})'.format(base2))
plt.show()
if __name__ == '__main__':
HalonSequence_test()base가 2, 3 인 경우를 각각 x,y축에 scattering 해 보면 (data개수는 2000개) 다음과 같습니다.
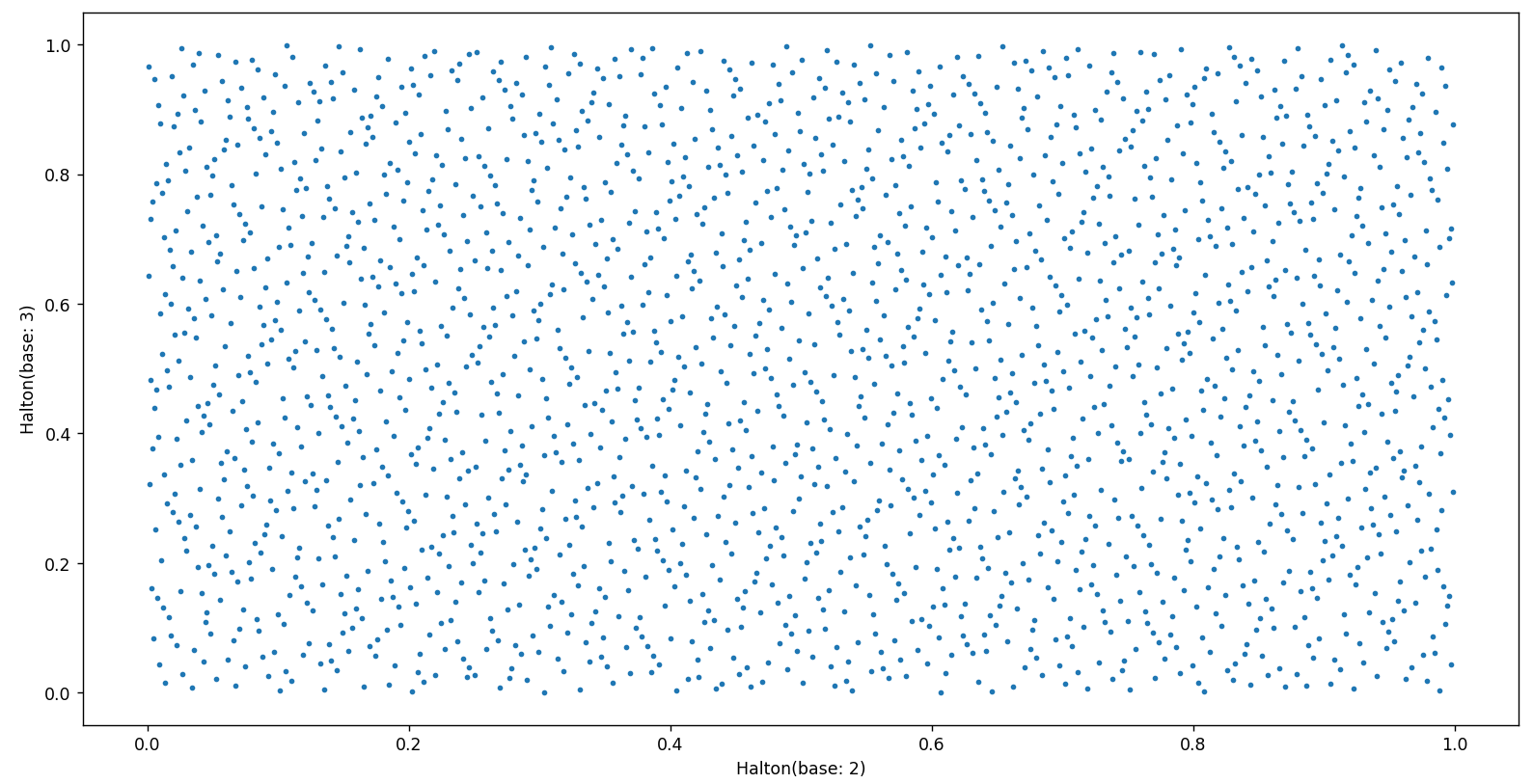
위에서 보았던 base가 17, 29에 대해서는 아래와 같이 나옵니다.
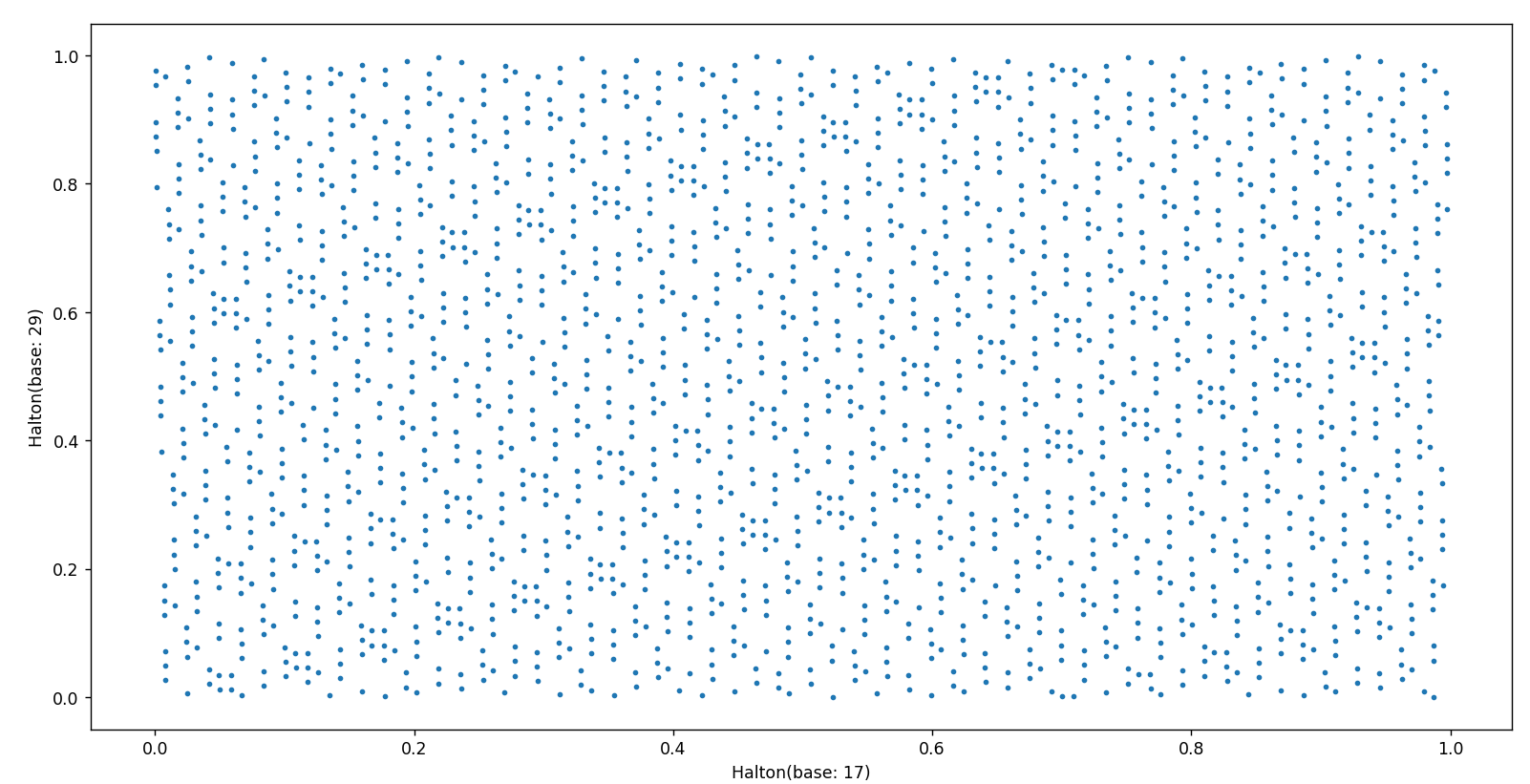
이제 균등 난수 생성은 이쯤에서 마치고 정규분포 난수를 생성하는 법을 소개해 볼까 합니다. 균등 분포 난수발생에서 Halton 방법과 쌍벽을 이루는 Sobol Sequence가 있는데요, 조만간 기회가 될 때 다뤄보도록 하겠습니다.
'수학의 재미 > 확률분포' 카테고리의 다른 글
| 정균분포 난수를 만들어 주세요 #1 : 중심극한정리 이용 (0) | 2022.06.13 |
|---|---|
| 중심극한정리: 평범한 것들은 정규분포이다. (0) | 2022.06.11 |
| 균등난수(uniform random number) 만들어보자 #2 : LCG (0) | 2022.06.10 |
| 균등난수(uniform random number) 만들어보자 #1 (0) | 2022.06.08 |
| Irwin-Hall Distribution (0) | 2022.05.25 |




댓글